자연어와 단어의 분산 표현

11 minute read

자연어와 단어의 분산 표현

NLP (Natural Language Processing, 자연어처리)는 텍스트에서 의미있는 정보를 분석, 추출하고 이해하는 일련의 기술집합입니다.
이러한 NLP를 활용항기 위하여 컴퓨터에게 단어의 의미를 이해시키는 것이 중요하다.
이러한 컴퓨터에게 자연어를 이해시키는 방법은 크게 3가지가 존재한다.

시소러스를 활용한 기법
통계 기반 기법
추론 기반 기법(word2vec)

시소러스를 활용한 기법

시소러스(Theaurus) 란 단어의 의미에 따라 분류, 배열한 일종의 유의어 사전 이다.

위의 그림같이 하나의 단어에 관한 동의어 혹은 반의어등 관련있는 단어를 모아놓은 하나의 사전이다.
이러한 Theaurus를 사용하게 되면 아래와 같은 3가지 문제점이 발생하게 된다.

시대 변화에 대응하기 어렵다.
단어의 의미가 시대에 변화하는 것을 포함시키기 어렵다.
사람을 쓰는 비용이 크다.
현존하는 영어 단어의 수만 해도 1000만개가 넘어가므로 이러한 방대한 단어 사이의 관계를 정의하는 것이 많은 시간과 노력이 필요한 작업이다.
단어의 미묘한 차이를 표현할 수 없다.
Theaurus는 뜻이 비슷한 단어들끼리 묶으므로 실제로 비슷한 단어들이도 미묘한 차이가 있는 것을 표현하지 못한다.

이러한 Theaurus를 사용하는 대표적인 방법이 WordNet이다.

WordNet

WordNet이란 위에서 설명한 Theaurus방법의 일종으로서 영어 어휘들 데이터 베이스라고 생각하면 된다.
이러한 WordNet은 python NLTK 라이브러리를 통하여 사용한다.

NLTK 설치

pip3 install nltk

NLTK 라이브러리 import

import nltk

WordNet에서 동의어 얻기 동의어는 nltk.corpus.wordnet에서 synsets() Method로서 사용된다. 아래 결과에 뜻은 car라는 단어에 다섯가지 서로다른 동의어가 정의되어있다는 것이다.
car.n.01의 의미를 살펴보게 되면

car: 단어이름
n: 속성(명사, 동사 등)
01: 그룹의 인덱스

#WordNet 다운로드
nltk.download('wordnet')

#wordnet에서 동의어 찾기
from nltk.corpus import wordnet
wordnet.synsets('car')

[Synset('car.n.01'),
 Synset('car.n.02'),
 Synset('car.n.03'),
 Synset('car.n.04'),
 Synset('cable_car.n.01')]

위의 결과에서 car1.n.01이 의미하는 것을 출력해보자
동의어 그룹에서 definition()을 통하여 결과를 확인할 수 있다.
definition()은 사람이 그 단어를 이해하고 싶을때 사용

car = wordnet.synset('car.n.01')
car.definition()

'a motor vehicle with four wheels; usually propelled by an internal combustion engine'

car1.n.01에 어떠한 단어들이 존재하는지 샆려보는 것은 lema_name()를 통해 이루어진다.

car.lemma_names()

['car', 'auto', 'automobile', 'machine', 'motorcar']

위에서 Wrodnet은 비슷한 단어들을 묶은 영어 사전이라고 정의하였다.
이러한 단어들은 포함관계로서 Vertical relationship이다.
car라는 단어를 포함하고 있는 상위 개념을 살펴보기 위하여 hypernym을 사용한 예제 결과를 살펴보게 되면 entity -> physical_entity -> … -> car로서 정의되어있다는 것을 알 수 있다.

car.hypernym_paths()[0]

[Synset('entity.n.01'),
 Synset('physical_entity.n.01'),
 Synset('object.n.01'),
 Synset('whole.n.02'),
 Synset('artifact.n.01'),
 Synset('instrumentality.n.03'),
 Synset('container.n.01'),
 Synset('wheeled_vehicle.n.01'),
 Synset('self-propelled_vehicle.n.01'),
 Synset('motor_vehicle.n.01'),
 Synset('car.n.01')]

WordNet은 또한 단어가 동의어 별로 그룹지어져 있기 때문에 단어 사이의 유사도를 계산할 수 있다.
유사도는 0 ~ 1 까지의 값을 가지며 값이 높을수록 의미가 비슷한 단어이다.
실행 결과 car, novel, dog, motorcycle 중에 car란 가장 유사한 의미를 가지고 있는 단어는 motorcycle이라는 것을 확인 할 수 있다.

#단어 정의
car = wordnet.synset('car.n.01')
novel = wordnet.synset('novel.n.01')
dog = wordnet.synset('dog.n.01')
motorcycle = wordnet.synset('motorcycle.n.01')

print(car.path_similarity(novel))
print(car.path_similarity(dog))
print(car.path_similarity(motorcycle))

0.05555555555555555
0.07692307692307693
0.3333333333333333

통계 기반 기법

통계 기법을 살펴보면서 말뭉치(corpus)를 사용한다.
말뭉치란 대량의 텍스트 데이터 이다. 맹목적으로 수집된 텍스트 데이터가 아닌 자연어 처리연구나 애플리케이션을 염두에 두고 수집된 텍스트 데이터를 일반적으로 말뭉치라고 칭한다.

말뭉치 전처리 과정을 텍스트 데이터를 단어로 분할하고 그 분할된 단어들을 단어 ID 목록으로 변환하는 일 이다.

말뭉치 전처리 과정: Text를 단어로 자른 뒤 고유의 ID를 붙여주는 과정이다.

text = 'You say goodbye and I say hello'
print('text 확인', text)
#소문자로 변경
text = text.lower()
#마침표 처리
text = text.replace('.', ' .')
#Text => Word
words = text.split(' ')
print('단어 확인',words)

#말뭉치 전처리 과정 Vocab 사전 만드는 과정
word_to_id = {}
id_to_word = {}

for word in words:
    if word not in word_to_id:
        new_id = len(word_to_id)
        word_to_id[word] = new_id
        id_to_word[new_id] = word
        
print('id_to_word 확인',id_to_word)
print('word_to_id 확인',word_to_id)

# Text 말뭉치 전처리 결과
import numpy as np
corpus = [word_to_id[w] for w in words]
corpus = np.array(corpus)
print('결과 확인', corpus)

text 확인 You say goodbye and I say hello
단어 확인 ['you', 'say', 'goodbye', 'and', 'i', 'say', 'hello']
id_to_word 확인 {0: 'you', 1: 'say', 2: 'goodbye', 3: 'and', 4: 'i', 5: 'hello'}
word_to_id 확인 {'you': 0, 'say': 1, 'goodbye': 2, 'and': 3, 'i': 4, 'hello': 5}
결과 확인 [0 1 2 3 4 1 5]

위의 과정을 한번에 해결하는 Method이다.
return 으로서 word_to_id, id_to_word, corpus를 Return하므로 위의 과정을 한번에 처리할 수 있다.

def preprocess(text):
    text = text.lower()
    text = text.replace('.', ' .')
    words = text.split(' ')

    word_to_id = {}
    id_to_word = {}
    for word in words:
        if word not in word_to_id:
            new_id = len(word_to_id)
            word_to_id[word] = new_id
            id_to_word[new_id] = word

    corpus = np.array([word_to_id[w] for w in words])

    return corpus, word_to_id, id_to_word

위에서 선언한 Method를 확인

text = 'You say goodbye and I say hello'
corpus, word_to_id, id_to_word = preprocess(text)
print('corpus: ',corpus)
print('word_to_id: ',word_to_id)
print('id_to_word: ',id_to_word)

corpus:  [0 1 2 3 4 1 5]
word_to_id:  {'you': 0, 'say': 1, 'goodbye': 2, 'and': 3, 'i': 4, 'hello': 5}
id_to_word:  {0: 'you', 1: 'say', 2: 'goodbye', 3: 'and', 4: 'i', 5: 'hello'}

단어의 전처리 과정 이후 단어를 Vector로서 표현하는 방식이 필요하다. 이러한 방식은 임베딩이라 불린다.
임베딩 사전 지식은 아래 링크를 참조하자.
임베딩 상세내용
이러한 수많은 임베딩 방식 중에 오늘 Post할 방법은 분포 가설이다.
분포 가설 이란 단어의 의미가 Text에서의 맥락에서 유추 가능하다라는 것 이다.
문맥 이라는 개념은 아래 사진참고하자

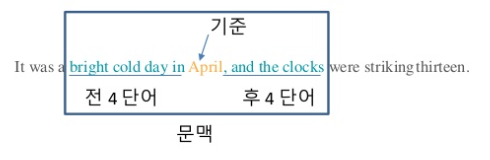
그림참조: 홍배 김
즉 문맥이란 하나의 Text에서 특정 단어를 중심에 둔 그 주변 단어를 의미한다.
여기서 주변 단어와 특정 단어와의 거리를 Window Size라고 표현한다.

이러한 분포 가설을 활용하여 단어를 Vector로 만드는 방법 중 하나가 동시 발생 행렬이다.
즉 주변 단어를 세어서 얼만큼 분포되어있는지를 확인하여 빈도로 표현하고 이를 벡터로 나타낸 것이다.
아래 Text에 대한 동시 발생 행렬을 정의하여 보자.
Text: you say goodbye and i say hello

	you	say	goodbye	and	i	hello	.
you	0	1	0	0	0	0	0
say	1	0	1	0	1	1	0
goodbye	0	1	0	1	0	0	0
and	0	0	1	0	1	0	0
i	0	1	0	1	0	0	0
hello	0	1	0	0	0	0	1
.	0	0	0	0	0	1	0

C = np.array([
    [0,1,0,0,0,0,0],
    [1,0,1,0,1,1,0],
    [0,1,0,1,0,0,0],
    [0,0,1,0,1,0,0],
    [0,1,0,1,0,0,0],
    [0,1,0,0,0,0,1],
    [0,0,0,0,0,1,0],
],dtype=np.int32)
print(C[0])
print(C[1])
print(C[2])

[0 1 0 0 0 0 0]
[1 0 1 0 1 1 0]
[0 1 0 1 0 0 0]

아래 Method는 위와 같은 과정을 수행하는 Method이다.

corpus: 말뭉치
vocab_size: vocab_size
window_size: window_size

def create_co_matrix(corpus, vocab_size, window_size=1):
    corpus_size = len(corpus)
    co_matrix = np.zeros((vocab_size, vocab_size), dtype=np.int32)

    for idx, word_id in enumerate(corpus):
        for i in range(1, window_size + 1):
            left_idx = idx - i
            right_idx = idx + i

            if left_idx >= 0:
                left_word_id = corpus[left_idx]
                co_matrix[word_id, left_word_id] += 1

            if right_idx < corpus_size:
                right_word_id = corpus[right_idx]
                co_matrix[word_id, right_word_id] += 1

    return co_matrix

이제 Text를 단어로서 만들고 그러한 단어를 Vector로서 표현할 수 있게 되었다.
이 Vector사이에 서로 얼만큼 유사한지는 코사인 유사도를 사용하게 된다.

코사인 유사도

코사인 유사도 식

$$similarity(x,y) = \frac{x y}{||x|| ||y||} = \frac{x_1y_1 + ... + x_ny_n}{\sqrt{x_1^2 + ... + x_n^2}\sqrt{y_1^2 + ... + y_n^2}}$$

위의 식은 -1 ~ 1의 값을 가지게 되고 각 값에 대한 그림은 아래와 같다.

즉 각각의 성분이 얼만큼 유사한지를 계산하는 과정이다.
좀 더 자세히 알아보게 되면 벡터의 내적의 연산 공식을 알면 된다.
아래와 같은 두 백터가 존재한다고 하였을때

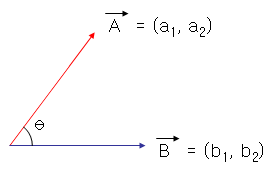
$$\vec{a} \bullet \vec{b}=|\vec{a}| |\vec{b}|cos\theta$$

$$|\vec{a}| = \sqrt{a_1^2 + a_2^2}, |\vec{b}| = \sqrt{b_1^2 + b_2^2}$$

$$\vec{a} \bullet \vec{b} = a_1b_1 + a_2b_2$$

따라서 아래와 같은 식이 성립하게 된다.

$$cos\theta = \frac{a_1b_1 + a_2b_2}{\sqrt{a_1^2 + a_2^2} \sqrt{b_1^2 + b_2^2}}$$

$cos\theta$ 를 그림으로 나타내면 아래와 같다.

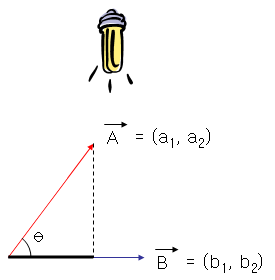
위의 그림에서도 알 수 있듯이 서로 Vector간에 성분을 얼만큼 표현하는 지에 관한 그림이 나오므로 이 말은 서로 얼만큼 같은 성분을 가지고 있냐?와도 같은 의미가 된다.

위의 식을 Code로서 나타내면 아래와 같다.

def cos_similarity(x, y, eps=1e-8):
    nx = x / (np.sqrt(np.sum(x ** 2)) + eps)
    ny = y / (np.sqrt(np.sum(y ** 2)) + eps)
    return np.dot(nx, ny)

eps는 아주 작은 값으로서 혹시나 0으로 나누는 과정이 없기 위한 값 이다.

위의 함수를 활용하여 Text= “You say goodbye and I say hello”에서 You와 I의 유사도를 비교하는 과정이다.

text = 'You say goodbye and I say hello.'
corpus, word_to_id, id_to_word = preprocess(text)
vocab_size = len(word_to_id)
C = create_co_matrix(corpus, vocab_size)

c0 = C[word_to_id['you']]  # "you"의 단어 벡터
c1 = C[word_to_id['i']]    # "i"의 단어 벡터
print(cos_similarity(c0, c1))

0.7071067691154799

위에서 선언한 Method를 개선하여 검색어와 가장 비슷한 단어를 추출하는 Method를 만들어보자.

query: 검색어
word_to_id: 단어에서 단어 ID로의 딕셔너리
id_to_word: 단어 ID에서 단어로의 딕셔너리
word_matrix: 단어 벡터들을 한데 모은 행렬, 각 행에는 대응하는 단어의 벡터가 저장되어있다고 가정
top: 상위 몇 개까지 추출할지에 관한 Parameter
argsort(): 배열에 담긴 원소의 인덱스를 내림차순으로 정리

def most_similar(query, word_to_id, id_to_word, word_matrix, top=5):
    if query not in word_to_id:
        print('%s(을)를 찾을 수 없습니다.' % query)
        return

    print('\n[query] ' + query)
    query_id = word_to_id[query]
    query_vec = word_matrix[query_id]

    # 코사인 유사도 계산
    vocab_size = len(id_to_word)

    similarity = np.zeros(vocab_size)
    for i in range(vocab_size):
        similarity[i] = cos_similarity(word_matrix[i], query_vec)

    # 코사인 유사도를 기준으로 내림차순으로 출력
    count = 0
    for i in (-1 * similarity).argsort():
        if id_to_word[i] == query:
            continue
        print(' %s: %s' % (id_to_word[i], similarity[i]))

        count += 1
        if count >= top:
            return
most_similar('you',word_to_id,id_to_word,C,top=5)

[query] you
 goodbye: 0.7071067691154799
 i: 0.7071067691154799
 hello: 0.7071067691154799
 say: 0.0
 and: 0.0

위와 같이 단어 사이의 거리만으로서 판단하는 것은 매우 큰 문제점이 발생하게 된다.
영어에서의 the와같이 많이 나오는 수식어는 자주 출몰하게되어서 모든 단어와의 거리가 가까워 지게 되고 이로 인하여 많은 단어와의 상관성이 높에 나올 수 있다.
이러한 문제점을 해결한 방안이 PMI이다.

PMI

PMI 식

$$PMI(x,y) = log_2 \frac{P(x,y)}{P(x)P(y)}$$

위의 식을 살펴보게 되면 P(x)는 x가 말뭉치에 등장할 확률을 가르키고 P(x,y)는 x와 y가 동시에 일어날 확률을 나타낸다.
즉 x 와 y가 나오는 각 시점에서 둘의 단어가 같이 나오면 이 단어의 상관성이 높다고 판단하는 것 이다.
C(x)가 x의 등장횟수이고 말뭉치에 포함된 단어 수를 N이라 하면 PMI의 식은 다음과 같다.
PMI 식

$$log_2 \frac{P(x,y)}{P(x)P(y)} = log_2 \frac{\frac{C(x,y)}{N}}{\frac{C(x)}{N}\frac{C(y)}{N}} = log_2 \frac{C(x,y)N}{C(x)C(y)}$$

위의 식에서의 문제는 P(x,y) = 0 인경우 $log_20 =-\inf$ 이므로 문제가 발생하게 된다. 위와 같은 문제를 해결한 것이 PPMI이고 아래 식과 같다.
PPMI 식

$$PPMI(x,y) = max(0,PMI(x,y))$$

위와 같은 식은 아래 Code로서 나타낼 수 있다.

def ppmi(C, eps = 1e-8):
    #동시 발생 행렬과 같은 크기의 행렬
    M = np.zeros_like(C, dtype=np.float32)
    #말뭉치에 포함된 단어 수
    N = np.sum(C)/2
    #각 단어의 발생 횟수
    S = np.sum(C, axis=0)
    
    for i in range(C.shape[0]):
        for j in range(C.shape[1]):
            #PMI 식
            pmi = np.log2(C[i, j] * N / (S[j]*S[i]) + eps)
            #PPMI 식
            M[i, j] = max(0, pmi)

    return M
W = ppmi(C)

#유효 자릿수를 3자리로 표시
np.set_printoptions(precision=3)
print('동시 발생 행렬')
print('-'*50)
print(C)
print('PPMI')
print(W)

동시 발생 행렬
[[0 1 0 0 0 0 0]
 [1 0 1 0 1 1 0]
 [0 1 0 1 0 0 0]
 [0 0 1 0 1 0 0]
 [0 1 0 1 0 0 0]
 [0 1 0 0 0 0 1]
 [0 0 0 0 0 1 0]]
--------------------------------------------------
PPMI
[[0.    0.807 0.    0.    0.    0.    0.   ]
 [0.807 0.    0.    0.    0.    0.    0.   ]
 [0.    0.    0.    0.807 0.    0.    0.   ]
 [0.    0.    0.807 0.    0.807 0.    0.   ]
 [0.    0.    0.    0.807 0.    0.    0.   ]
 [0.    0.    0.    0.    0.    0.    1.807]
 [0.    0.    0.    0.    0.    1.807 0.   ]]

위와 같은 방법에도 문제가 있다.
말뭉치의 어휘 수가 증가함에 따라 각 단어 벡터의 차원 수도 증가한다는 문제이다.

SVD

위와 같은 문제를 위하여 차원감소 방법중에 SVD를 사용한다.
SVD에 자세한 내용은 아래 링크 참조
SVD 자세한 내용
위와 같은 식은 numpy의 ilnalg Module을 사용하여 구현한다.

import matplotlib.pyplot as plt

# SVD
U, S, V = np.linalg.svd(W)

print('동시 발생 행렬')
print(C[0])
print('-'*10)
print('PPMI')
print(W[0])
print('-'*10)
print('SVD')
print(U[0])

# 플롯
for word, word_id in word_to_id.items():
    plt.annotate(word, (U[word_id, 0], U[word_id, 1]))
plt.scatter(U[:,0], U[:,1], alpha=0.5)
plt.show()

동시 발생 행렬
[0 1 0 0 0 0 0]
----------
PPMI
[0.    1.807 0.    0.    0.    0.    0.   ]
----------
SVD
[ 0.000e+00  3.409e-01 -3.886e-16 -1.205e-01  9.323e-01 -1.110e-16
 -1.467e-16]

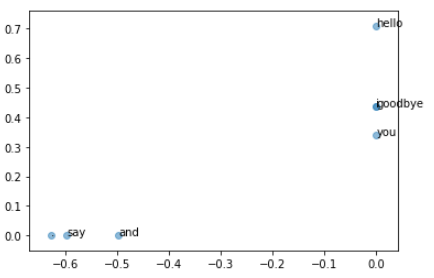
PTB 데이터 셋을 활용, sklearn의 SVD를 활용하여 선언한 Method의 결과를 확인하여 보자.

from dataset import ptb


window_size = 2
wordvec_size = 100

corpus, word_to_id, id_to_word = ptb.load_data('train')
vocab_size = len(word_to_id)
print('동시발생 수 계산 ...')
C = create_co_matrix(corpus, vocab_size, window_size)
print('PPMI 계산 ...')
W = ppmi(C)

print('calculating SVD ...')
try:
    # truncated SVD (빠르다!)
    from sklearn.utils.extmath import randomized_svd
    U, S, V = randomized_svd(W, n_components=wordvec_size, n_iter=5,
                             random_state=None)
except ImportError:
    # SVD (느리다)
    U, S, V = np.linalg.svd(W)

word_vecs = U[:, :wordvec_size]

querys = ['you', 'year', 'car', 'toyota']
for query in querys:
    most_similar(query, word_to_id, id_to_word, word_vecs, top=5)

동시발생 수 계산 ...
PPMI 계산 ...

동시발생 수 계산 ...
PPMI 계산 ...
calculating SVD ...

[query] you
 i: 0.700317919254303
 we: 0.6367185115814209
 anybody: 0.565764307975769
 do: 0.563567042350769
 'll: 0.5127798318862915

[query] year
 month: 0.6961644291877747
 quarter: 0.6884941458702087
 earlier: 0.6663320660591125
 last: 0.6281364560127258
 next: 0.6175755858421326

[query] car
 luxury: 0.6728832125663757
 auto: 0.6452109813690186
 vehicle: 0.6097723245620728
 cars: 0.6032834053039551
 corsica: 0.5698372721672058

[query] toyota
 motor: 0.7585658431053162
 nissan: 0.7148030996322632
 motors: 0.6926157474517822
 lexus: 0.6583304405212402
 honda: 0.6350275278091431

이런 SVD를 사용하면 차원이 준다는 장점이 있지만 시간이 오래 걸린다는 단점이 생기게 된다.

참조: 원본코드
참조: metashower 블로그
참조: 밑바닥부터 시작하는 딥러닝2
코드에 문제가 있거나 궁금한 점이 있으면 wjddyd66@naver.com으로 Mail을 남겨주세요.

Share on

Twitter Facebook LinkedIn

JeongYong Hwang

자연어와 단어의 분산 표현