CNN (1) CNN이란

CNN

CNN(Convolutional Neural Network)을 알기 전에 우선적으로 Convolution이란 무엇인지 알아야 한다.

Convolution

Convolution이란 합성 곱이다. Convolution의 식은 아래와 같다.

$$x(t) \ast h(t) = \int_{- \infty}^\infty x( \tau)t(x - \tau)d\tau$$

그림출처:위키피디아
이러한 Convolution은 추력값이 어떠한 한 시점에만 영향을 받는 것이 아니라, 이전의 입력 값들에도 영향을 받기 때문에 단순한 곱셈이 아닌 합성곱 형태로 나타내는 것이다.
또한 결과값이 클 수록 서로 같은 성분을 많이 가지고 있는것을 위의 그림에서 알 수 있다.

그렇다면 이러한 CNN을 왜 Image 처리에서 많이 사용하는지 생각해보자.
먼저 Computer에서 Image는 (가로, 세로, Channel)로서 3차원으로 인식하게 된다.
즉, Image를 각각의 픽셀로서 구성하고 RGB값을 입혀서 인식하게 된다.
이러한 Image는 공간적인 정보가 담겨 있다.
예를 들어 공간적으로 가까운 픽셀은 값이 비슷하거나, RGB의 각 채널은 서로 밀접하게 관련되어 있거나, 거리가 먼 픽셀끼리는 별 연관이 없는 등, 3차원 속에서 의미를 갖는 본질적인 패턴이 숨겨져있을 것이라고 추측할 수 있다.
이러한 Image를 그저 Affine 계층처럼 1차원으로 행렬을 변환해서 Input Data로서 해결하는 것은 이러한 정보를 살릴 수 없다.
따라서 이러한 Image의 특징을 살리면서 Hidden Layer에 3차원으로 데이터로 전달하기 위하여 CNN을 사용하게 된다.

CNN 구성

위의 개념인 Convolution을 활용하여 Neural Network를 어떻게 구성하는 지에 대해 알아보자.

(1) Kernel
Image(Input)에 Weigth를 곱하는 과정에서 Convolution이 일어나게 된다.
CNN에서는 이러한 Weight를 Kernel이라고 한다.
대표적으로 많이 사용되는 Kernel은 아래와 같다.

출처위키피디아
Image(Input) 28 x 28 이 망을 통과하는 과정을 살펴보자.
Kernel의 크기는 5 x 5라고 가정을 하게 되면

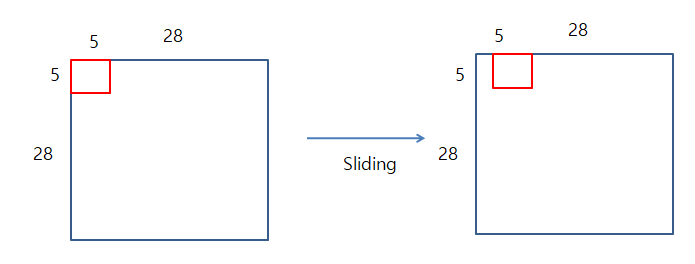
위의 이미지처럼 28 x 28 Image에 5x5의 Kernel를 1칸씩 Sliding하면서 Fetch 의 범위안의 값들을 서로 곱한뒤 더해주는 과정이 일어나게 된다.
이러한 과정을 Convolution이라고 불리게 된다.
Kernel이 몇칸씩 이동하는 지는 사용자가 지정할 수 있고 이러한 이동하는 간격은 Stride라고 한다.

위와 같은 과정은 이전까지의 ANN에서 가중치만 생각한 것이다.
ANN에서의 Bias까지 생각하게 되면 Convolution의 최종적인 과정은 아래 그림과 같다.

위와 같이 CNN Model을 설계할 때 차원의 크기를 생각하는 것이 매우 중요하다.
아래와 같은 가정이 있을때 간단한 수식을 사용하여 Output의 차원의 크기를 쉽게 예측할 수 있다.

• 입력 크기: (H, W)
• 필터 크기: (FH, FW)
• 출력 크기: (OH, OW)
• 패딩: P
• 스트라이드: S

$$OH = \frac{H + 2P - FH}{S} + 1$$

$$OW = \frac{W + 2P - FW}{S} + 1$$

3차원 데이터(RGB) 합성곱 연산
위에서 Computer가 인식하는 Image는 (가로, 세로, Channel)이라고 하였다.
위에서는 Channel = 1인 흑백 Image의 Convolution의 대해서만 생각하였다.
아래 그림은 Channel = 3인 Color Image에 대한 Convolution에 대한 과정이다.

여기서 입력 데이터와 Fiter의 Channel의 수가 같아야 된다는 것을 알 수 있다.

이러한 3차원 Image Convolution에 대한 계산 과정을 블록으로 생각하면 아래 그림과 같다.

위에서 Filter는 ANN에서의 Weight라고 생각할 수 있다고 하였다.
그렇다면 CNN에서의 여러개의 Feature를 가진 Filter를 생각하여 Convolution을 실행한 결과는 아래 그림과 같다.

즉 Output을 한장의 OFM 이라고 생각하게 되면 Filter의 개수가 OFM의 Channel의 수가 된다는 것을 확인 할 수 있다.

위의 과정을 전부 적용시킨 결과는 아래 이미지와 같다.

Batch 처리
마지막으로 Model의 Trainning시간을 줄이기 위하여 계속하여 Batch처리를 한다.
CNN에서의 Batch 처리를 하게 되면 3차원의 Image 여러개가 하나의 묶음으로서 들어가게 되어 4차원의 Data가 된다고 생각할 수 있다.
이러한 4차원은 그림으로서 표현할 수 없어 아래 그림과 같이 N개의 데이터라는 표시로서 3차원 + 1차원 으로서 4차원일 경우의 Convolution 결과 차원을 나타내고 있다.

(2) Activation map
Convolution을 최종적으로 마친 값은 아래 그림과 같다.
이러한 결과를 Activation map이라고 불리게 된다.

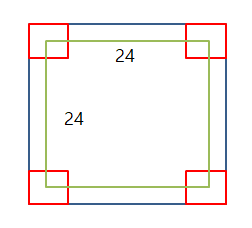
28 x 28의 Image가 Convolution을 통해 최종적인 24 x 24의 Image로 축소하게 된다.
이미지가 축소되는 것을 방지하기 위하여 이미지 둘레에 특정 값을 둘러쌀 수 가 있는데 이를 Padding이라고 불리게 된다.


하나의 Weight가 아닌 모든 Weight를 적용하게 된다면 아래 그림과 같이 일어나게 된다.

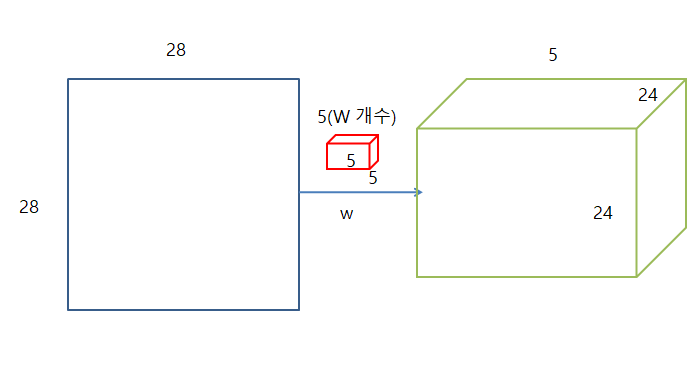
• 원본 Image: 28 x 28
• Weiht: 5 x 5 x 5(Weight의 개수)
• Sliding: 1칸씩
• 처리 결과: 24(28-5+1) x 28 x 5(Weight개수)

(3) ReLU
Feature Map에서 양의 값만을 활성화시키는 레이어이다.
Feature Map에서 특히나 두드러지는 특징을 다시 추출하는 역할을 한다.
Convolution의 특성을 위에서 이렇게 정의하였다.
결과값이 클 수록 서로 같은 성분을 많이 가지고 있는것을 위의 그림에서 알 수 있다.
즉, 큰 값일 수록 중요하기 때문에 5이상의 값에서 Gradinet값이 0으로 가까워지는 단점을 극복한 ReLU를 사용한다.
ReLU 사용이유

(4) Pooling
위의 과정을 거친 다음 Pooling을 통해 값을 Reduce하는 과정이 일어난다.

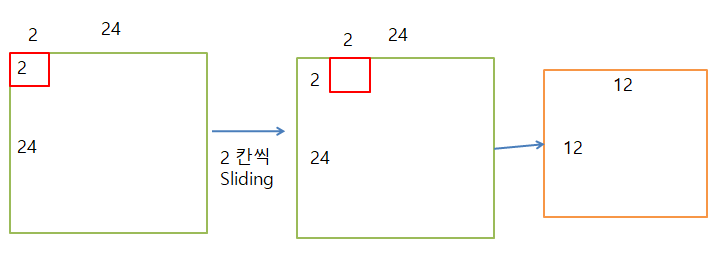
• 처리결과: 24 x 24
• Pooling: 2 x 2
• Sliding: 2칸씩
• 처리 결과: 12(24/2) x 12

Pooling을 통해 24 x 24를 12 x 12인 반으로 Reduce하는 과정이 일어나게 된다.
Pooling의 종류로는 최댓값을 뽑아내는 max pooling, 평균값을 뽑아내는 mean pooling등 다양한 종류가 존재한다.
Pooling의 사용이유 크게 3가지로 나눌 수 있다.

1. 정발 꼭 필요한 데이터만 뽑아낼 수 있다.
2. 데이터의 양이 작아진다.
3. Feature가 많아질 경우 Overfitting발생을 예방하기 위해서이다.

또한 이러한 Pooling Layer는 다음과 같은 특징을 가진다.

1. 학습해야 할 매개 변수가 없다.
2. 채널 수가 변하지 않는다.
3. 입력의 변화에 영향을 적게 받는다.

이러한 최종적인 과정을 그림으로서 표현하면 아래와 같다.

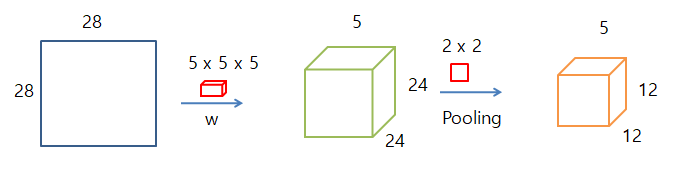
(5) Dropout
Dropout은 Overfitting을 막기위한 방법으로 뉴럴 네트워크가 학습중일때, 랜덤하게 뉴런을 꺼서 학습함으로써, 학습이 학습용 데이터로 치우치는 현상을 막아준다.

그림출처:leonardoaraujosantos
일반적으로 CNN에서는 이 Dropout Layer를 Fully connected Network(모든 Filter 와 Pooling 작업을 한 과정) 뒤에 놓지만, 상황에 따라서는 Pooling Layer뒤에 놓기도 한다.
아래 그림은 Dropout 적용과 적용하지 않은 Model사이의 예측 정확도를 비교한 결과이다.

(6) Output(Softmax Function)
최종적인 결과를 확인하기 위해서 Softmax Function으로서 Classification을하게 된다.
Softmax자세한 내용
최종적인 CNN의 그림은 아래와 같다.

그림출처:bcho 블로그

(7) 참고사항 CNN에 대한 추가적인 몇가지에 대해 알아보자.

정확도를 더 높이려면?
CNN Model을 만드는데에 대하여 정확도를 높이는 방법은 몇가지가 존재한다.
1. 데이터 확장
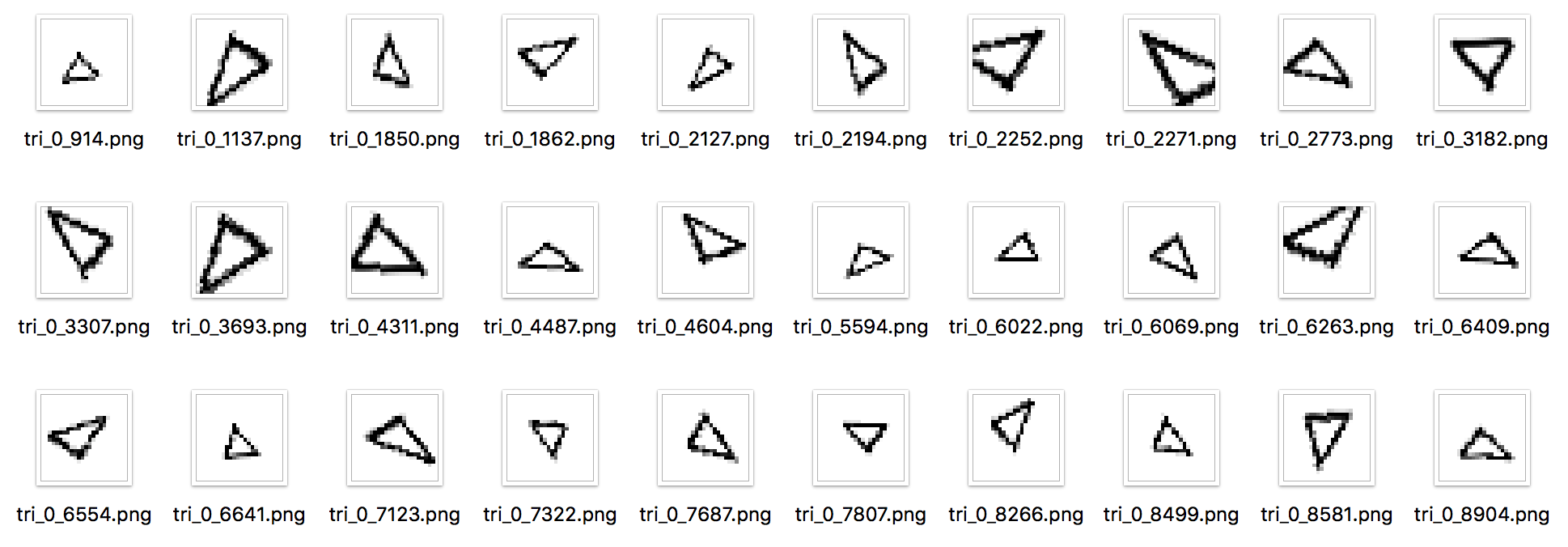
데이터 확장(Data augmentation)은 입력 이미지를 알고리즘을 동원해 ‘인위적’으로 확장한다.
입력 이미지를 회전하거나 세로로 이동하는 등 미세한 변화를 주어 이미지의 개수를 늘리는 것이다.
이는 데이터가 몇 개 없을 때 특히 효과적인 수단이다.
아래 그림은 데이터 확장에 대한 예시이다.

2. Hidden Layer를 깊게

1. 층의 깊이에 비례해 정확도가 좋아지는 것.
2. 신경망의 매개변수 수가 줄어든다는 것이다.
   층을 깊게 한 신경망은 깊지 않은 경우보다 적은 매개변수로 같은(혹은 그 이상) 수준의 표현력을 달성할 수 있다.
3. 작은 필터를 겹쳐 신경망을 깊게 할 때의 장점은 매개변수 수를 줄여 넓은 수용 영역(receptive field)을 소화할 수 있다는 데 있다.(수용 영역은 뉴런에 변화를 일으키는 국소적인 공간 영역이다.)
4. ReLU 등의 활성화 함수를 합성곱 계층 사이에 끼움으로써 신경망의 표현력이 개선된다.이는 활성화 함수가 신경망에 “비선형” 힘을 가하고, 비선형 함수가 겹치면서 더 복잡한 것도 표현할 수 있게 되기 때문이다.
5. 학습 효율성도 좋아진다.
   층을 깊게 함으로써 학습 데이터의 양을 줄여 학습을 고속으로 수행할 수 있다는 뜻이다.
   층이 깊어지면 학습해야 할 문제를 계층적으로 분해할 수 있다.
   각 층이 학습해야 할 문제를 더 단순한 문제로 대체할 수 있는 것이다.

CNN BackPropagation

CNN을 아래와 같은 그림으로 같단히 나타내어 보자.

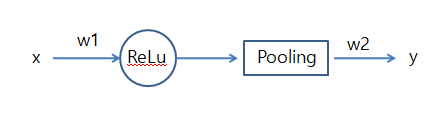
위와 같은 CNN에서 ReLU와 Polling과정을 하나의 Hidden Layer라고 생각을 하면 다음과 같은 식을 얻을 수 있다.

$$\delta^{n} = W \delta^{n+1} \ast g\prime(x) $$

하지만 Weigt를 곱해주는 것은 Convolution을 통하여 이루어지기 때문에 위의 식은 아래와 같이 표현할 수 있다.

$$\delta^{n} = W \ast \delta^{n+1} \circ g\prime(x) (g(x): ReLu Function)$$

CNN에서는 Pooling과정을 커치기 때문에 서로 Size가 달라서 SizeScaling 과정이 필요하게 된다.
SizeScaling같은 경우 Kronecker Product를 통하여 이루어지게 된다.
아래 과정은 Kronecker Product의 과정이다.

$$\begin{bmatrix} 1 & 2\\3 & 4 \end{bmatrix} x \begin{bmatrix} 4 & 5\\6 & 7 \end{bmatrix} = \begin{bmatrix} 1x4 & 2x4 & 1x5 & 2x5 \\ 3x5 & 4x5 & 3x5 & 4x5 \\ 1x6 & 2x6 & 1x6 & 2x6 \\ 1x7 & 2x7 & 1x7 & 2x7 \end{bmatrix}$$

이 된다.
이러한 Kronecker Product을 CNN에서 사용할때 1의 원소를 가지고 있는 행렬로서 SizeScaling을 하게 되면 아래와 같은 식이 된다.

$$\begin{bmatrix} a & b\\c & d \end{bmatrix} x \begin{bmatrix} 1 & 1\\1 & 1 \end{bmatrix} = \begin{bmatrix} a & a & a & a \\ b & b & b & b \\ c & c & c & c \\ d & d & d & d \end{bmatrix}$$

위의 Kronecker Product 과정을 up()으로 간단하게 표현하게 되고 다시 식으로서 나타내게 되면 아래와 같다.

$$\delta^{n} = W \ast \delta^{n+1} \circ up(g\prime(x))$$

---

참조: Chanwoo Timothy Lee Youtube
참조: 냠냠 블로그
참조:leonardoaraujosantos
참조: Chanwoo Timothy Lee Youtube
참조:bcho 블로그
문제가 있거나 궁금한 점이 있으면 wjddyd66@naver.com으로 Mail을 남겨주세요.