Theory2. Fundamentals of Machine Learning

2. Fundamentals of Machine Learning

\(\newcommand{\argmin}{\mathop{\mathrm{argmin}}\limits}\) Machine Learning의 기초적인 이론부분을 다시 제대로 잡고 싶어서 문일철 교수님의 인공지능 및 기계학습 개론을 정리한 Post입니다.

• 2.1 Rule Based Machine Learning
• 2.2 Decision Tree
• 2.3 Entropy and Information Gain
• 2.4 Linear Regression

2.1 Rule Based Machine Learning

Rule Basec Machine Learning을 사용하기 위하여 다음과 같은 Dataset이 존재한다고 생각해보자.

Sky	Temp	Humid	Wind	Water	Forecast	EnjoySpt
Sunny	Warm	Normal	Strong	Warm	Same	Yes
Sunny	Warm	High	Strong	Warm	Same	Yes
Rainy	Cold	High	Strong	Warm	Change	No
Sunny	Warm	High	Strong	Cool	Change	Yes

위의 Dataset에서 Sky ~ Forecast까지는 Feature로서 Input으로 Model에 들어가는 Dataset이고 EnjoySpt는 예측하고자하는 Label이라고 표현하자.(단, Feature는 2가지의 Category만을 포함한다고 생각하자.)

위와 같은 Dataset과 사용할 Model, 또한 Hypothese H를 다음과 같이 용어 정리를 하고 넘어가자.

• Instance X
  • Features: O: <Sunny, Warm, Normal, Strong, Warm, Same>
  • Label: Y: Yes.
• Training Dataset D: A collection of observations on instance
• Hypotheses H
  • Potentially posiible function to turn X into Y
  • \(h_i\): <Summy, Warm, ?, ?, ?, Same> -> Yes
  • Hypothesis는 Catoegory 2 + Don’t Care(?)의 값을 가질 수 있다. 따라서 최대 \(3^6\)의 개수가 될 수 있다.
• Target Function c
  • Unknown target function between the features and the label

위와 같은 용어로서 정리하자면, Machine Learning이라는 학문을 다음과 같이 설명할 수 있다.
Machine Learning이란 Model(Hypothese)를 Training Dataset을 통하여 Model을 훈련하여 Hypothesis를 Target Function에 맞추는 작업이다. 이러한 작업을 Function Approximation이라고 한다. 이러한 결과로서 Instanxe X의 Feature가 Model에 Input으로 들어오면, Output으로서 Label을 Prediction한다.

위의 말을 간략하게 하면, 결국 Dataset을 활용하여 Model을 만들고 Feature를 통하여 Label을 Prediction하는 것을 의미한다.

위의 훈련이라는 과정은 다음과 같은 2개의 문제를 Solve하기 위해서 사용된다.

1. Hypothesis를 몇개 사용하여야 하는가?
2. Hypothsis를 어떻게 정의하여야 하는가?

위의 문제를 풀기 위하여 특정 Model인 Rule Based Model에 맞춰서 생각해 보자.

위와 같은 Rule Based Model를 구성하기 위해서는 Find-S Algorithm(Rule)을 사용하여 구성한다.

Find-S Algorithm

if x is positive:
    for feature f in O:
        If fiin h == fiin x:
            Do nothing
        else:
            fiin h = fiin h ∪ fiin x

위의 Algorithm을 Rule Based Model와 위에서 정의한 Example로서 살펴보자.
앞으로의 Step은 Data가 들어오는 경우를 의미하게 된다.

Step 0
Rule Based Model를 구성하는 최초 Hypothesis는 2개로 구성된다.

$$S_0 = {<\varnothing,\varnothing,\varnothing,\varnothing,\varnothing,\varnothing>}$$

$$G_0 = {}$$

위의 두개의 Hypothesis를 설명하면 \(S_0\)는 제일 Specific한 Hypothesis로서 모든 조건을 거부하는 Hypothsis이다. \(G_0\)는 제일 General한 Hypothesis로서 모든 조건을 허용하는 Hypothsis이다.

Rule Based Model는 결국 $S_0$는 좀 더 Generalize하게 만들고, $G_0$는 좀 더 Specific하게 만들어서 Target Function을 찾아내는 것 이다.

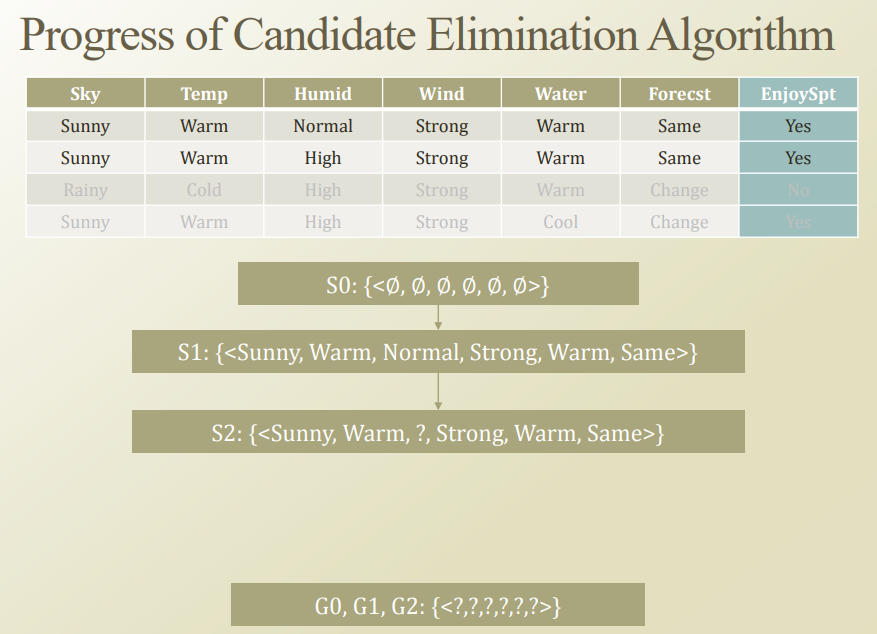
Step 1,2

위의 Step1과 Step2를 각각 생각하면 다음과 같다.

먼저 Dataset 1이 들어오게 되었을 경우 Specific한 Hypothesis(\(S_0\))에 의하여 Label은 False로서 판단된다. 이러한 결과는 틀렸으므로 Find-S Algorithm에 의하여 \(S_0 \cup <Sunny,Warm,Normal,Strong,Warm,Same> = S_1\)으로서 결정된다.

Step2의 경우도 Step1과 같은 결과로서 결과가 나오게 된다.

Step3
위의 결과를 살펴보면, Generalize Hypothsis를 통하여 Dataset 3(\(<Rainy, Cold, High, Strong, Warm, Change>\))가 Yes라고 판단되게 된다.
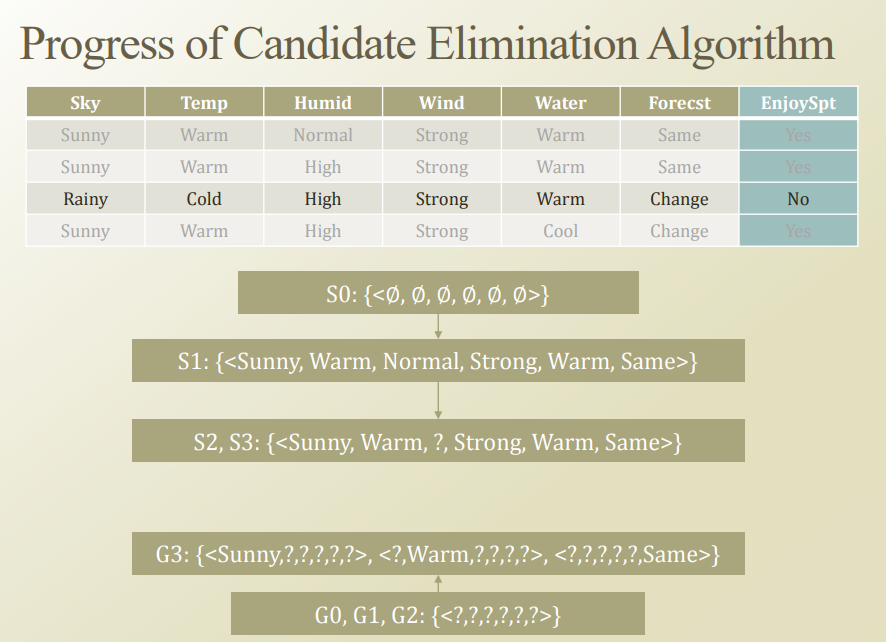
따라서 Label과 일치하지 않기 때문에 Generalize Hypothesis를 바꾸에서 Dataset 3이 False로서 판단되게 바꾸어야 한다.

Step4 최종적인 Dataset이 들어오게 되었을 경우 Step 1,2,3과 같은 과정으로 인하여 새롭게 Generalize Hypothsis와 Specific Hypothesis를 Trainin하였다.

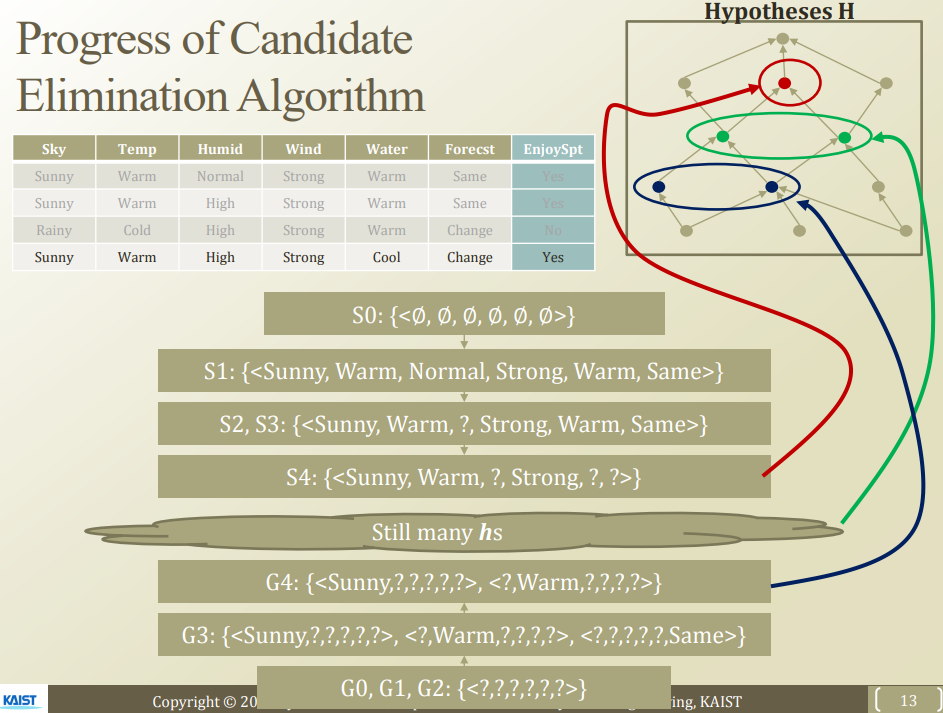
이 두가지의 사이에서 다음과 같이 다양한 Hypothesis가 생성될 수 있다. 여전히 많은 Hypothesis가 있다는 것을 알 수 있다.

결국 Target Function을 찾을 수 없었지만 그에 가깝게 Rule Based Model의 Hypothesis를 Approximation하였다는 것을 알 수 있다.

문제점

1. 실제 Data는 Noise가 포함된다. -> 실제 Hypothesis가 False로 변할 수 있다.
2. Observasation Error -> 모든 Data를 통하여 Model을 구축 할 수 없다.
3. Decision Factor(Dataset Feature)를 잘못 설정할 수 있다.

2.2 Decision Tree

Decision Tree는 다음과 같이 WIKI에서 정의하고 있다.

결정 트리(decision tree)는 의사 결정 규칙과 그 결과들을 트리 구조로 도식화한 의사 결정 지원 도구의 일종이다. 결정 트리는 운용 과학, 그 중에서도 의사 결정 분석에서 목표에 가장 가까운 결과를 낼 수 있는 전략을 찾기 위해 주로 사용된다.

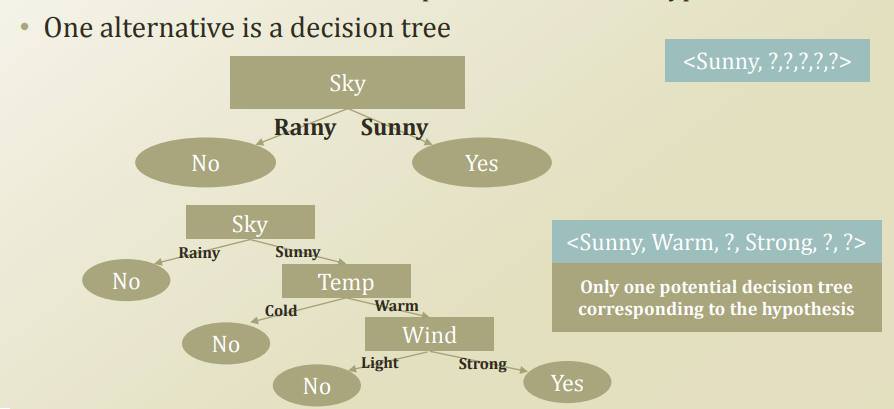
즉, 위에서는 Rule Based Model은 결국 Hypothesis로서 표현하였다.
Decision Tree는 Rule Based Model과 Hypothsis를 Tree구조로서 만든 것 이다.(결국 같은 Algorithm이다.)

의문을 가져야 하는 것은 Rule Based Algorithm에서 문제점으로서 실제 Data는 Noise가 포함되고, 완벽하게 분리할 수 없다고 하였다.
따라서 100% Accuracy를 갖출수 없는 Model이라면, 결국 어떻게 Model을 평가하는지, 이러한 평가 결과로서 어떤 Model이 더 좋은 Model인지 판단 할 수 있어야 한다.

2.3 Entropy and Information Gain

Entropy

위의 의문에 대하여 Model을 평가할 수 있는 방법으로서 Entropy방법을 사용한다.

먼저 Model의 성능이 좋다는 것은 다음과 같은 의미가 있다.

• Reducing the most uncertainty

Entropy란 이러한 불확실성을 측정하는 방법이다. Higher Entropy라는 것은 이러한 Uncertainty가 높다는 의미이고 식으로서 표현하면 다음과 같다.

$$H(X) = -\sum_{x}P(X=x)log_{b}P(X=x)$$

1장에서 배운 Bayes Rule(Conditional)을 추가한 Conditional Entropy를 식으로서 나타내면 다음과 같이 표현할 수 있다.

$$H(Y|X) = \sum_X P(X=x)H(Y|X=x)$$

$$=\sum_X P(X=x){- \sum_Y P(Y=y|X=x)log_b P(Y=y|X=x)}$$

Entropy를 살펴보면 다음과 같다.
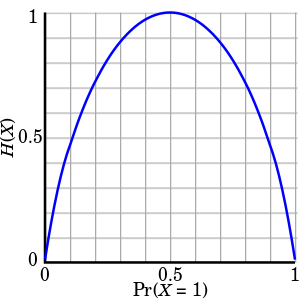
사진 출처: WIKI

만약 동전던지기로서 살펴보면, P(X)는 앞면이 나올 확률, P(Y)는 뒷면이 나올 확률이면 P(X) = P(Y)인 지점 즉, P(X) = 1/2인 지점에서 Entropy는 최대화가 되고, 불확실성이 가장 낮다고 판단한다.
P(X) = 1, P(Y) = 0인 지점에서는 Entropy는 0의 값이 나오게 되고, Uncertainty가 높다고 판단한다.

Information Gain

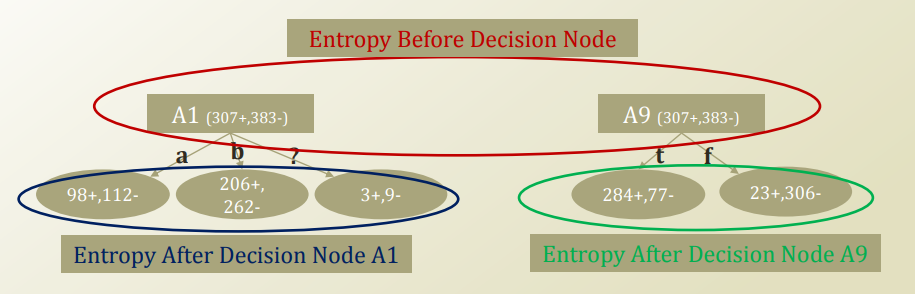
이제 Decision Tree에 적용하기 위하여 다음과 같은 예제를 살펴보자.

위를 살펴보게 되면 A1, A9는 둘다 307개를 +, 383개를 -로 판단된다.
이러한 기존의 Hypothesis의 Entropy는 다음과 같이 나타낼 수 있다.

$$H(Y) = -\sum_{Y \in {+,-}} P(Y=y)log_2P(Y=y)$$

위와 같은 과정에서 각각의 Decision Tree에 대하여 Conditional Entropy를 적용하면 다음과 같은 결과로서 나타낼 수 있다.

$$H(Y|A1) = \sum_{X \in {a,b,?}} \sum_{Y \in {+,-}} P(A1=x,Y=y)log_2 \frac{P(A1=x)}{P(A1=x,Y=y)}$$

$$H(Y|A9) = \sum_{X \in {t,f}} \sum_{Y \in {+,-}} P(A9=x,Y=y)log_2 \frac{P(A9=x)}{P(A9=x,Y=y)}$$

이러한 Conditional Entropy와 Entropy의 차이를 Information Gain이라고 한다.

$$IG(Y,A_i) = H(Y) - H(Y|A_i)$$

즉, Information Gain이 많을 수록 Conditional Entropy의 값이 높을 것 이다.

이러한 결과로서 모든 Hypothesis에 대하여 Information Gain을 구할 수 있고, Information Gain이 높은 것 부터 Decision Tree에서 중요한 위치(Root)에 가깝게 위치시킬 수 있다.

Decision Tree를 점점 더 크고 깊게 만들수록 Training Dataset에 대하여 Accuracy가 점점 증가하겠지만 Test Dataset에서는 성능이 안 좋을 수 있다. 이렇게 Training Dataset에 너무 Fitting되는 것을 Overfitting이라고 얘기하며, 이러한 Overfitting이 무엇인지, 어떻게 해결하는지는 좀 더 후에 알아보도록 하자.

2.4 Linear Regression

Linear Regression의 하나의 Hypothesis를 다음과 같이 정의할 수 있다.

$$H: \hat{x;\theta} = \theta_0 + \sum_{i=1}^{n} \theta_i x_i = sum_{i=1}^{n} \theta_i x_i$$

Linear Regression은 이러한 Feature가 Linear하게 Label과 연관되어 있어서 \(\theta\)를 통하여 Feature와 Label의 관계를 잘 Lienar한 관계로서 나타내는 것 이다.

먼저 \(\theta\)를 잘 표현하기 위해서 다음과 같이 가정하자.

• \(f = X\theta + e\): e(Error)를 포함한 실제 Function
• \(\hat{f} = X\theta\): Error는 포함하지 않아서 실제 Function과 차이가 있으나, 우리가 찾고자하는 Function(Hypothesis)

결국 우리는 Linear한 관계가로 생각한다면 \(\theta\)값만 변경하여서 \(\hat{f}\)를 설정할 수 있다. (Function Approximation)

따라서 최적의 \(\theta\)를 \(\hat{\theta}\)라고 한다면 다음과 같이 식을 적용할 수 있다.

$$\hat{\theta} = \argmin_{\theta}(f-\hat{f})^2 = \argmin_{\theta}(Y - X\theta)^2$$

$$= \argmin_{\theta}(Y-X\theta)^{T}(Y-X\theta)$$

$$= \argmin_{\theta}(\theta^{T}X^{T}X\theta - 2\theta^{T}X^{T}Y)$$

위의 식을 살펴보게 되면 2차 함수로서 Convex한 Function인 것을 확인할 수 있다.
따라서, \(\theta\)에 대하여 미분하여 0인 Point를 찾으면 그 Point는 최솟값을 가지는 Point라는 것을 알 수 있다. 따라서 위의 식을 좀 더 진행하면 다음과 같다.

$$\bigtriangledown_{\theta}(\theta^{T}X^{T}X\theta - 2\theta^{T}X^{T}Y) = 0$$

$$2X^{T}X\theta - 2X^{T}Y) = 0$$

$$\theta = (X^{T}X)^{-1}X^{T}Y$$

$$\therefore \hat{\theta} = (X^{T}X)^{-1}X^{T}Y$$

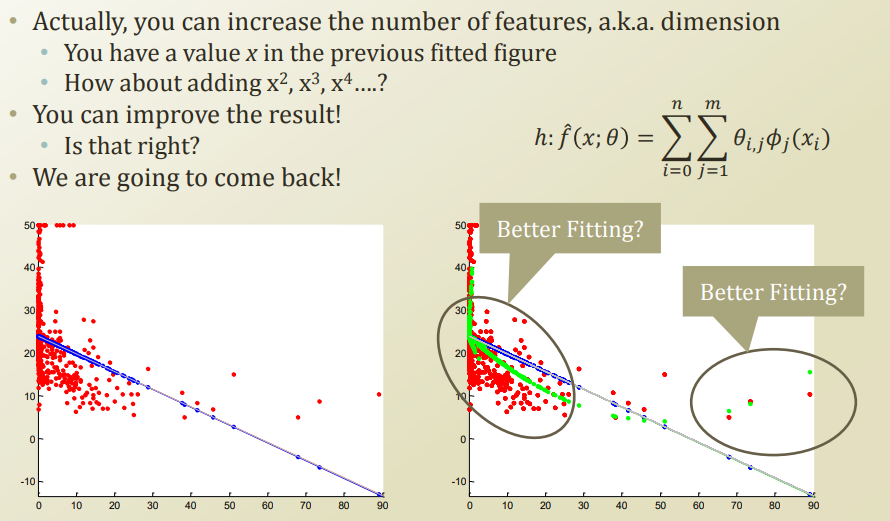
위의 Linear Regression의 문제점은 무엇일까?
아래 그림을 살펴보면 알 수 있다.

왼쪽의 그림을 보면 Linear한 Regression만으로는 선형적으로 분류하기 때문에 Model이 잘 분류할 수 없다고 한다.

따라서, Linear Regression에 Non Linearity를 좀 더 추가하여 나타내면 다음과 같이 나타낼 수 있다. (오른쪽 그림)

$$h: \hat{f}(x;\theta) = \sum_{i=0}^{n} \sum_{j=1}^{m} \theta_{i,j} \varnothing_j(x_i)$$

$$\varnothing_n(x) = x^n$$

즉 Dataset의 자승을 하는 것을 Feature로서 사용하여 Non Linearity를 증가(Weight 개수 증가)시키게 하여 Model의 성능을 높이게 되고 이러한 형태를 Multivariate Linear Regression

Decision Tree와 마찬가지로 Model의 크기를 증가시킴에 따라서 Training Dataset에 대하여 Accuracy가 증가할 수 있으나, Overfitting이 발생할 수 있다는 단점이 발생하게 된다.