Theory3. Naive Bayes Classifier

3. Naive Bayes Classifier

\(\newcommand{\argmin}{\mathop{\mathrm{argmin}}\limits}\) \(\newcommand{\argmax}{\mathop{\mathrm{argmax}}\limits}\) Machine Learning의 기초적인 이론부분을 다시 제대로 잡고 싶어서 문일철 교수님의 인공지능 및 기계학습 개론을 정리한 Post입니다.

• 3.1 Optimal Classification
• 3.2 Conditional Independence
• 3.3 Naive Bayes Classifier

3.1 Optimal Classification

위의 사진은 Classifier의 그림을 나타내고 있다.
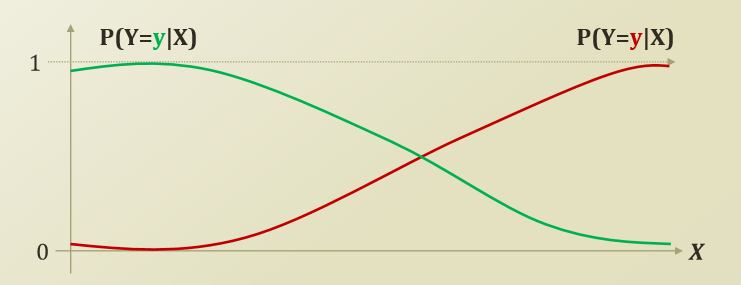
X(Feature)가 주어진 상황에서 Y(Label)일 확률에 대하여 보여주고 있다.(Label은 o or 1로서 Category Value, Discrete한 형태를 보여주고 있다.)

위와 같은 상황에서 Optimal predictor of Bayes classifier는 다음과 같은 식으로서 정의된다.

$$f^{*} = \argmin_f P(f(X) \neq Y) = \argmin_f P(\hat{y} \neq Y)$$

위의 식을 살펴보면 지난번의 Post에서의 Linear Regression의 Function Approximation과 같은 꼴인 것을 알 수 있다.
위의 식을 argmin -> argmax로서 식을 변형하면 다음과 같이 나올 수 있다.(Label이 2개인 경우)

$$f^{*} = \argmax_{Y=y} P(Y=y|X=x)$$

그렇다면 이러한 Bayes Classifier를 사용하기 전왜 왜 Bayes Classifier를 사용하는지 알아야 한다.

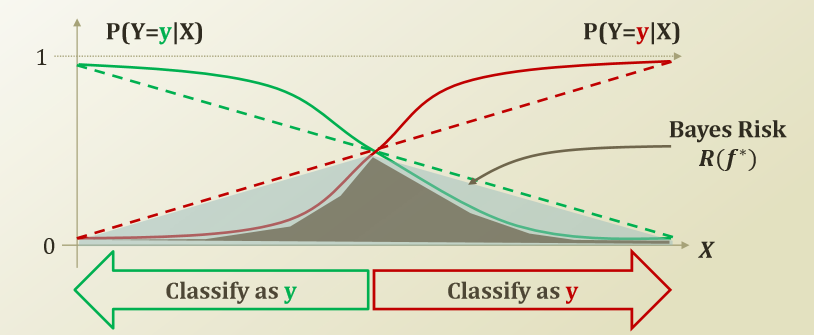
위와 같이 Non-Linear한 Classifier를 사용하지 않고 Linear한 Classifier로서 사용하면 다음과 같다.

위의 그림은 실제 Linear한 Classifier와 Non Linear한 Classifier는 Bayes Risk만큼 Error의 차이가 발생하는 것을 확인할 수 있다.
Bayes Classifier란 결국 Bayes Risk를 최대한 줄이는 Classifier이다.(Non Linear)

Bayes Classifier의 Risk를 줄이기 위하여 1장에서 배운 MLE, MAP를 활용하여 위의 식을 Function Approximation하여 Target Function과 비슷한 형태로 만드는 것을 목표로 하자.

잠깐 MAP의 식을 다시 살펴보면 다음과 같다.

$$P(\theta|D) = \frac{P(D|\theta)P(\theta)}{P(D)}$$

$$Posterior = \frac{Likelihood*PriorKnowledge}{Normalizing Constant}$$

$$P(\theta|D) \varpropto P(D|\theta)P(\theta)$$

위의 식을 Optimal predictor of Bayes classifier에 적용하면 다음과 같다.

$$f^{*} = \argmax_{Y=y} P(Y=y|X=x) = \argmax_{Y=y}P(X=x|Y=y)P(Y=y)$$

위의 식을 사용하기 위해서는 다음과 같은 사전 정보가 필요하다.

• Prior = Class Prior = P(Y=y)
• Likelihood = Class Conditional Density = P(X=x|Y=y)

위와 같은 문제는 Dataset이 주어졌을 경우 쉽게 구할 수 있다.
하지만, X가 여러개의 Feature를 가지고 있을 경우 문제가 복잡해지는 것을 알 수 있다.

이러한 여러개의 Feature로서 Combination결과인 많은 X에 대하여 Prediction하는 Model이 Naive Bayes Classifier이다.

3.2 Conditional Independence

지난번에 사용하였던 Dataset을 통하여 위의 식이 얼마나 걸리는지 확인하여 보자.

Sky	Temp	Humid	Wind	Water	Forecast	EnjoySpt
Sunny	Warm	Normal	Strong	Warm	Same	Yes
Sunny	Warm	High	Strong	Warm	Same	Yes
Rainy	Cold	High	Strong	Warm	Change	No
Sunny	Warm	High	Strong	Cool	Change	Yes

Dataset이 위와 같이 존재한다고 할때 \(\argmax_{Y=y}P(X=x|Y=y)P(Y=y)\)를 계산하기 위하여 몇개의 Parameter가 필요한지 알아보자.

• \(P(Y=y)\): k-1, k: Label Category 개수
• \(P(X=x|Y=y): (2^d -1)k\), d는 Feature 개수

위의 식을 살펴보게 되면 Feature의 개수에 따라서 \(P(X=x|Y=y)\)가 Exponential 하게 증가하기 때문에 Dataset을 구축하기 매우 어렵고 Model을 Training하기 매우 어렵다는 것을 알 수 있다.

따라서 위의 식을 좀 더 간편하게 바꾸어야 한다.
좀 더 간편하기 바꾸기 위하여 Conditional Independence라고 가정하는 것 이다. 즉 Feature 끼리는 서로 Independent할 것이라고 가정하는 것 이다.

Feature끼리 Conditional Independent라고 가정하게 되면, 식이 다음과 같이 성립할 수 있다.

$$P(X=<x_1,x_2,...,x_n>|Y=y) \rightarrow \prod_{i=1}^n P(X_i=x_i|Y=y)$$

$$\because P(x_1|x_2, y) = P(x_1|y) \rightarrow P(x_1,x_2|y) = P(x_1|y)P(x_2|y)$$

$$(x_1\text{ is conditionally independent of }x_2 \text{ given y)}$$

위의 식을 조금 생각해보면, 즉 \(x_1\)은 \(x_2\)에 영향을 받지 않고(서로 Independent) y에 의해서만 영향을 받는다 라고 해석할 수 있다.

위와 같이 Feature끼리 Conditional Independent하다고 가정하게 된다면, \((2^d -1)k \rightarrow (2-1)dk\)로서 Exponential한 복잡도에서 Polynomial한 복잡도로서 변하는 것을 확인할 수 있다.

3.3 Naive Bayes Classifier

위에서 최적화 하고자 하는 Function에 Conditional Independence를 적용하여 보자.

$$f^{*} = \argmax_{Y=y} P(Y=y|X=x) = \argmax_{Y=y}P(X=x|Y=y)P(Y=y)$$

$$\approx \argmax_{Y=y}\prod_{i=1}^n P(X_i=x_i|Y=y)P(Y=y)$$

Conditional Independet라고 가정하였기 때문에 Approx하다고 가정할 수 있다는 것 이다.

문제점

1. Naive Assumption: 우리가 Conditional Independent라고 가정하고 만들었기 때문에 어쩔 수 없는 한계이다.
2. Incorrect Probability Estimations: 너무 Dataset이 Sparse하여 우리가 Dataset을 관측 하지 못하였다고 한다면 Model이 잘 작동하지 않을 것 이다.(MLE -> MAP 사용)

2의 경우는 모든 Model에서 적용되는 문제이다. 1의 경우는 결국에는 어쩔 수 없이 발생하는 문제라는 것을 알 수 있다.