Theory4. Logistic Regression

4. Logistic Regression

\(\newcommand{\argmin}{\mathop{\mathrm{argmin}}\limits}\) \(\newcommand{\argmax}{\mathop{\mathrm{argmax}}\limits}\) Machine Learning의 기초적인 이론부분을 다시 제대로 잡고 싶어서 문일철 교수님의 인공지능 및 기계학습 개론을 정리한 Post입니다.

• 4.1 Decision Boundary
• 4.2 Introduction to Logistic Regression
• 4.3 Logistic Regression Parameter Approximation 1
• 4.4 Gradient Method
• 4.5 Logistic Regression Parameter Approximation 2

4.1 Decision Boundary

지난 Post Naive Bayes Classifier를 사용하면 Non Linear한 형태로서 S Curve형태로 Bayes Risk를 Linear한 Model에 비하여 줄일 수 있었으나, Conditional Independence하다는 가정을 했었어야 했다.

Logistic Regression은 S Curve형태로 Non Linear한 형태인 것은 같으나, Conditional Independence하다는 가정없이 설계하는 Model이다.

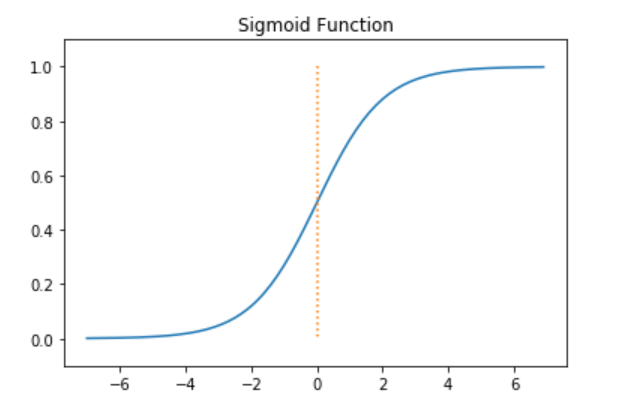
Non Linear한 형태를 가지는 다양한 함수가 존재하나 이번 Logistic Regression에서 Sigmoid Function을 사용하여 설계한다고 생각하자.

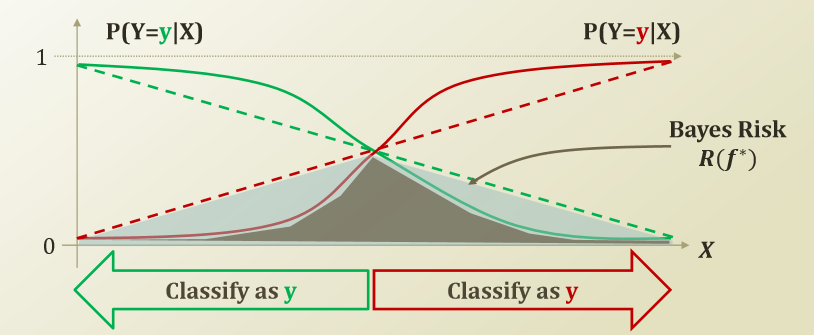
먼저 Decision Boundary가 무엇인지에 대하여 알아보자. 지난번에 사용하였던 사진을 살펴보면 다음과 같다.

Decision Boundary란 \(P(Y=y|X) = P(Y=y|X)\)가 만나는 지점으로서 Model이 Label을 Prediction하는 값이 바꾸는 부분이다.(그림에서는 중앙이라고 생각하자.)

Logistic Function에서 사용하는 Sigmoid는 다음과 같은 형태이다.

$$f(x) = \frac{e^{\beta_0+\beta_1x}}{1+e^{\beta_0+\beta_1x}}$$

위와 같은 Sigmoid Function을 사용하게 되면 Decision Boundary에서 급격하게 증가하는 Bayes Risk를 줄일 수 있다는 것을 알 수 있다.

4.2 Introduction to Logistic Regression

Logestic Regression의 식을 \(f(x) = \frac{e^{\beta_0+\beta_1x}}{1+e^{\beta_0+\beta_1x}}\)로서 정의하였다.

위의 식을 조금 더 생각하면 다음과 같이 생각할 수 있다.
\(\beta_0, \beta_1\)을 사용하여 Weight로서 사용하게 되면 Feature와 Weight가 Lienar한 어떤 관계가 있다고 생각할 수 있고, 이러한 결과를 None Linear한 Sigmoid Function을 사용하여 0~1사이의 확률값으로서 나타내는 것 이다.

위의 식을 Logit변환인 \(log(\frac{x}{1-x})\)를 사용하여 나타내면 결국 \(\beta_0 + \beta_1 x\)의 값이 나오게 된다.

최종적으로 생각하게 되면, 0~1사이의 확률값을 나타내는 Sigmoid Function을 Logit 변환을 하면 결국 Linear한 관계의 식을 얻을 수 있다. 식으로서 표현하면 다음과 같다.

$$log(\frac{p}{1-p}) = X\theta$$

이제 일반적인 Logestic Regression의 특징 및 Function Approximation을 위하여 다음과 같은 상황에서 Logestic Regression을 적용하여 보자.

Given Bernoulli experiment

$$p(y|x) = u(x)^{y}(1-u(x))^{1-y}$$

$$u(x) = P(y=1|x) = \frac{1}{1+e^{-\theta^{T}x}}\text{: Logestic Function}$$

$$X\theta = log(\frac{u(x)}{1-u(x)})$$

위의 식에서 우리고 모르는 값은 \(\theta\)값 이므로 이러한 \(\theta\)값을 추정해 나가는 것이 Function Approximation이라는 것을 알 수 있다.

4.3 Logistic Regression Parameter Approximation 1

위의 식에서 Prior 정보는 없으므로 MLE로서 Function Approximation을 수행하게 된다.
여기에서 이전 Conditional Independence의 개념을 적용시킨 Maximum Conditional Likelihood Estimation(MCLE)를 진행한다. (Feature를 여러개라고 생각한다.)

MCLE

$$\hat{\theta} = \argmax_{\theta} P(D|\theta) = \argmax_{\theta} \prod_{i=1}^N P(Y_i|X_i ;\theta)$$

위의 식에서 log변환을 하게 되면 Multiply형식이 아니라 Sum의 형식으로 나타낼 수 있다.

$$ = \argmax_{\theta} log(\prod_{i=1}^N P(Y_i|X_i ;\theta)) = \argmax_{\theta} \sum_{i=1}^N log(P(Y_i|X_i ;\theta))$$

위의 식에서 위에서 정의한 Bernoulli Experiment상황이라 생각하면, \(p(y|x) = u(x)^{y}(1-u(x))^{1-y}\)을 대입할 수 있다.

$$log(P(Y_i|X_i ;\theta)) = Y_i log(u(X_i)) + (1-Y_i)log(1-u(x))$$

$$=Y_i log(\frac{u(X_i)}{1-u(X_i)})+log(1-u(X_i))$$

위의 식에서 우리는 \(u(x)\)를 Logestic Function이라고 가정하였고, 이로인한 Logit 변환을 \(X\theta = log(\frac{u(x)}{1-u(x)})\)라고 정의하였다. 따라서 식은 다음과 같이 변환된다.

$$=Y_iX_i\theta - log(1+e^{X_i\theta})$$

$$\therefore \hat{\theta} = \argmax_{\theta}\sum_{i=1}^{N}(Y_iX_i\theta - log(1+e^{X_i\theta}))$$

위의 식에서 argmax값을 구하기 위하여 미분을 실시하면 다음과 같다.

$$\frac{\partial}{\partial \theta_j}(\sum_{i=1}^{N}(Y_iX_i\theta - log(1+e^{X_i\theta})))$$

$$=(\sum_{i=1}^{N}Y_iX_{i,j})+(-\sum_{i=1}^{N}\frac{e^{X_i\theta}X_{i,j}}{1+e^{X_i\theta}})$$

$$=\sum_{i=1}^{N}X_{i,j}(Y_i-\frac{e^{X_i\theta}}{1+e^{X_i\theta}})$$

$$=\sum_{i=1}^{N}X_{i,j}(Y_i-P(Y_i=1|X_i;\theta)) = 0$$

위의 식은 더이상 전개하거나 풀기가 힘들게 되었다.
따라서 이전까지 사용하지 않았던 Gradient Method를 활용하여 Function Approximation을 진행하여야 한다.

4.4 Gradient Method

Gradient Method를 알기 위해서는 먼저 Taylor Expantion에 대해서 알아야 한다.

Taylor Expantion

미적분학에서, 테일러 급수(Taylor series)는 도함수들의 한 점에서의 값으로 계산된 항의 무한합으로 해석함수를 나타내는 방법이다.

식으로서 나타내면 다음과 같다.

$$f(x) = f(a) + \frac{f^{'}(a)}{1!}(x-a) + \frac{f^{''}(a)}{2!}(x-a)^2 + ...$$

$$= \sum_{n=0}^{\infty} \frac{f^{n}(a)}{n!}(x-a)^n$$

사인 함수의 테일러 급수의 수렴. 검은 선은 사인 함수의 그래프이며, 색이 있는 선들은 테일러 급수를 각각 1차(빨강), 3차(주황), 5차(노랑), 7차(초록), 9차(파랑), 11차(남색), 13차(보라) 항까지 합한 것이다.
참조: WIKI

Gradient Descent/Ascent
위의 Taylor Expantion을 활용하여 Gradient Method에 적용하여 보자.
먼저 Gradient Method라는 것은 Function에서 특정한 Point에서 원하는 Point로 가는 방법이다. 이러한 원하는 Point로 가기 위해서 어떤 방향(\(u\))로 갈지 그 방향으로 얼만큼의 속도(\(h\))로 이동할 지 알아야 한다.

위의 Taylor Series를 Big-Oh Notation을 사용하여 나타내면 다음과 같다.

$$f(x) = f(a) + f^{'}(a)(x-a)+O(||x-a||^2) $$

그렇다면 Gradient Method를 적용하기 위하여 현재 Point가 x_1이라고 가정하고 방향과 속도를 고려한 Vector(\(hu\))로서 point가 변경하는 것을 Taylor Series에 적용하여 생각하면 다음과 같다.

$$f(x_1+hu) = f(x_1)+hf^{'}(x_1)u + h^2 O(1)$$

$$\because u = \text{Unit Vector}$$

위의 식에서 우리는 h를 원하는 속도라고 지정하였다.
이것은 Learning Rate로서 사용자가 직접 정하는 Constant이며 매우 낮은 값으로서 설정한다.
따라서 위의 식을 다시한번 정리하면 다음과 같이 나타낼 수 있다.(제곱인 수는 매우 작아서 다른 수에 비해서 의미가 없을 정도로 작은 값이 될 것이라는 가정.)

$$f(x_1 + hu) - f(x_1) \approx h f^{'}(x_1)u$$

따라서, 최종적인 u에 대해서 Gradient Descent를 생각하면 다음과 같다.

$$u^{*} = \argmin_{u} f(x_1 + hu) - f(x_1) = \argmin_{u} h f^{'}(x_1)u$$

위의 식을 생각하면 기존의 값인 \(f(x_1)\)은 값이 크고, 이동한 값은 \(f(x_1 + hu)\)크면은 제일 Optimizer한 형태일 것 이다.

즉, Gradient Descent는 기존의 F의 값을 줄이는데 사용하는 방법이다. 위의 식에서 h는 Constant이고 u는 UnitVector이므로 다시 식을 생각하면 다음과 같이 정리된다는 것을 알 수 있다.

$$u^{*} \approx \argmin_{u}f^{'}(x_1)u$$

\(f^{'}(x_1)u\)는 두 Vector의 내적이고, 서로 180도 다른 경우 가장 작은 값이 나오게 될 것이다. 따라서 UnitVector인 u는 다음과 같이 표현될 수 있다.

$$u^{*} = -\frac{f^{'}(x_1)}{|f^{'}(x_1)|}$$

따라서 Gradient Descent를 활용하여 x값을 변형시키면 다음과 같이 나타낼 수 있다.

$$x_{t+1} \leftarrow x_{t} + hu^{*} = x_t -h\frac{f^{'}(x_1)}{|f^{'}(x_1)|}$$

Gradient Ascent의 경우 Descent의 반대 방향이라고 생각하면 된다. 즉, argmin이 아닌 argmax로서 서로 같은 방향일때 두 내적은 같은 값을 가지므로 다음과 같이 표현할 수 있다.

$$x_{t+1} \leftarrow x_{t} + hu^{*} = x_t + h\frac{f^{'}(x_1)}{|f^{'}(x_1)|}$$

4.5 Logistic Regression Parameter Approximation 2

위에서 더이상 식이 진행 불가능하였던 Logestic Regression의 식을 살펴보면 다음과 같다.

$$\hat{\theta} = \argmax_{\theta}\sum_{i=1}^{N}(Y_iX_i\theta - log(1+e^{X_i\theta}))$$

$$\frac{\partial}{\partial \theta_j}(\sum_{i=1}^{N}(Y_iX_i\theta - log(1+e^{X_i\theta})))$$

$$=\sum_{i=1}^{N}X_{i,j}(Y_i-P(Y_i=1|X_i;\theta)) = 0$$

더이상 진행 불가능한 상황에서 Gradient Ascent를 적용하려면 다음과 같다.

$$\theta_j^{t+1} = \theta_{j}^t + h \frac{\partial f(\theta^t)}{\partial \theta_j^t} = \theta_{j}^t + h({\sum_{i=1}^{N}X_{i,j}(Y_i-P(Y_i=1|X_i;\theta))})$$

$$= \theta_j^{t} + \frac{h}{C} (\sum_{i=1}^{N} (X_{i,j}(Y_i - \frac{e^{X_i \theta^t}}{1+e^{X_i \theta^t}})))$$

Linear Regression Revisited
Linear Regression을 Normal Equation으로서 해결하면 다음과 같은 Function Approximation을 할 수 있었다.

$$\hat{\theta} = (X^{T}X)^{-1}X^{T}Y$$

위의 Normal Equation의 문제점은 Dataset(X)의 값이 커지면 커질 수록 \((X^{T}X)^{-1}\)와 행렬의 곱 등 많은 연산에서 과부하가 걸릴 확률이 매우 높아 진다. 이러한 Linear Regression은 Gradient Descent를 사용하여 다시 식을 정리하면 다음과 같다.

$$\hat{\theta} = \argmin_{\theta}(f-\hat{f})^2 = \argmin_{\theta} \sum_{i=1}^{N} (Y^{i} - \sum_{j=1}^{d} X_j^i \theta_j)^2$$

$$\frac{\partial}{\partial \theta_k}\sum_{i=1}^{N} (Y^{i} - \sum_{j=1}^{d} X_j^i \theta_j)^2 = -\sum_{i=1}^{N}2(Y^{i} - \sum_{j=1}^{d} X_j^i \theta_j)X_{k}^i$$

Gradient Descent식에 대입하여 생각하면 다음과 같다.

$$\theta_{k}^{t+1} \leftarrow \theta_k^t -h \frac{\partial f(\theta^t)}{\partial \theta_k^t} = \theta_k^t + h\sum_{i=1}^{N}2(Y^{i} - \sum_{j=1}^{d} X_j^i \theta_j)X_{k}^i$$