Theory5. SVM(1)

5. SVM

\(\newcommand{\argmin}{\mathop{\mathrm{argmin}}\limits}\) \(\newcommand{\argmax}{\mathop{\mathrm{argmax}}\limits}\) Machine Learning의 기초적인 이론부분을 다시 제대로 잡고 싶어서 문일철 교수님의 인공지능 및 기계학습 개론을 정리한 Post입니다.

• 5.1 Decision Boundary with Margin
• 5.2 Maximizing the Margin
• 5.3 Soft Margin with SVM
• 5.4 Comparison to Logistic Regression

5.1 Decision Boundary with Margin

SVM이란 Classification의 일종이다.

SVM이란 이러한 상황에서 수많은 Decision Boundary에서 각각의 가장 가까운 Point 사이의 거리(Margin)을 최대화 하는 것 이다.

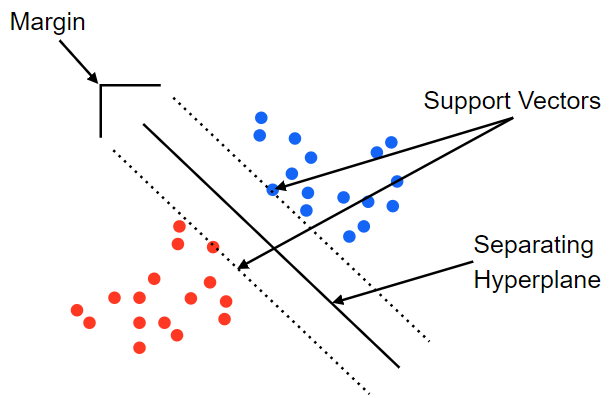
사진 출처: medium.com

수식으로 나타내면 다음과 같다.

$$f(x) = wx+b$$

Point가 x가로 하는 경우 Decision Boundary(Hyperplane)는 \(f(x) = wx+b=0\)으로 잡을 수 있다.

만약, Support Vector의 값이 \(f(x) = wx+b=a\)라면, Input Point에 따라서 \(a>0\)이면 Positive, \(a<0\)이면 Negative로서 판단할 수 있다.

5.2 Maximizing the Margin

Margin을 Maximizing하기 위하여 먼저 Margin을 구하여보자.
먼저 위의 그림을 다시 한번 생각하고 용어를 정리하여 보자.

• \(x_p\): Hyperplane위의 Point
• \(f(x) = wx+b = a \text{ or } -a\): Support Vector
• \(w\): Hyperplane의 접선 Vector
• $r$: Hyperplane의 에서 Support Vector 까지의 거리

위와 같이 가정하였을 경우 다음과 같이 x를 정의할 수 있다.

$$x=x_p + r\frac{w}{||w||}$$

즉, 임의의 한 Point는 Hyperplane위의 Point를 기준으로 방향은 w, 크기는 r인 Vector로서 표현할 수 있는 것 이다.

위의 식을 활용하면 다음과 같다.

$$f(x) = w(x_p + r \frac{w}{||w||})+b = r||w|| (\because f(x_p) = wx_p+b = 0)$$

$$\therefore r = \frac{f(x)}{||w||} \rightarrow \text{margin} = \frac{2a}{||w||}$$

위에서 Support Vector의 값을 a라고 하였으므로 다음과 같이 표현할 수 있다.

$$max_{w,b}2r = \frac{2a}{||w||}$$

$$s.t(wx_j+b)y_j \ge a$$

위의 식에서 a는 임의의 상수이므로 a=1이라 가정하면 최종적인 Maximizing the Margin은 다음과 같이 나타낼 수 있다.

\(min_{w,b}||w||\) \(s.t.(wx_j+b)y_j \ge 1\)

이러한 방법은 Hard Margin이라고 불리게 된다. Hard Margin이란 Linear한 Line으로서 어떻게든 Data를 분류한다는 의미이다.

아래와 같은 Data Point 분포가 있을 경우 문제를 생각해 보자.

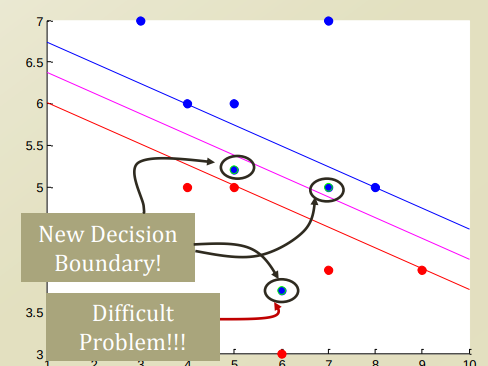
Decision Boundary와 Classify의 기준이 되는 Line사이의 Data Point가 들어오는 경우, 혹은 Linear한 Line으로는 도저히 분류할 수 없는 상황 등이 있다.

위와 같은 Error상황에서 크게 2가지의 해결방안이 있다.

1. Soft Margin: Error를 어느정도 허용하고 Linear하게 분류한다.
2. Kernel Trick: Non Linear하게 분류한다.

5.3 Error Handling in SVM

위에서 두가지 방법에 대하여 다음과 같이 정의 할 수 있다.

1. Soft Margin

• Admin there will be an “error”
• Represent the error in our problem formulation
• Try to reduce the error as well

2. Kernel Trick

• Make decision boundary
• more complex
• Go to non-linear

Soft Margin과 Kernel Trick둘다, 위에서 선언한 \(min_{w,b}||w||, s.t(wx_j+b)y_j \ge 1\)로서는 Error를 해결할 수 없으므로 Error에 관한 값을 Penalty Function으로서 나타내고 Penalty Function의 값 또한 Minimize하는 값을 찾아서 Classify하게 한다는 것 이다.

즉, 어느정도 Error는 허용하나 그 Error가 최소화되게 만든다는 의미이다.

Penalty Function을 선언하는 방법은 2가지가 있다.

Option 1

$$min_{w,b}||w||+C*(\text{Num of Error})$$

$$s.t(wx_j+b)y_j \ge 1$$

위의 식을 살펴보게 되면 Error의 개수 * C(임의의 상수)만큼 Penalty를 준다는 것 이다.
이러한 Penalty Function은 0-1 Loss라고 부르게 된다.
0-1 Loss란 Hyperplane까지는 Penalty가 없으나 반대쪽의 Support Vector를 넘어가는 순간 1의 Penalty를 주는 Penalty Function이다. 하지만, 이러한 Function은 거리와 상관없이 Count만으로서 Penalty를 주기 때문에 정확한 방법이라고 할 수 없다.

Option2

$$min_{w,b}||w||+C\sum_{j}\xi_j$$

$$s.t(wx_j+b)y_j \ge 1-\xi_j$$

$$\xi_j \ge 0$$

$$\text{EX) } \xi_j =(1-(wx_j+b)y_j)_{+}$$

위의 식을 살펴보게 되면 \(\xi\)는 Distance에 따라 \(\xi_j\)만큼 Penalty를 주겠다는 의미이다.
0-1 Loss에서의 문제점이였던, 거리에 따른 가중치를 주지 않는 것은 해결하였다. 이러한 Loss Function은 Hinge Loss라고 불린다. 하지만, C라는 Constant를 정의해야 하는 새로운 문제가 발생하게 되었다.

위의 Option1,2의 Penalty Function을 SVM에 적용하여 Visualizatio하면 다음과 같이 나타낼 수 있다.

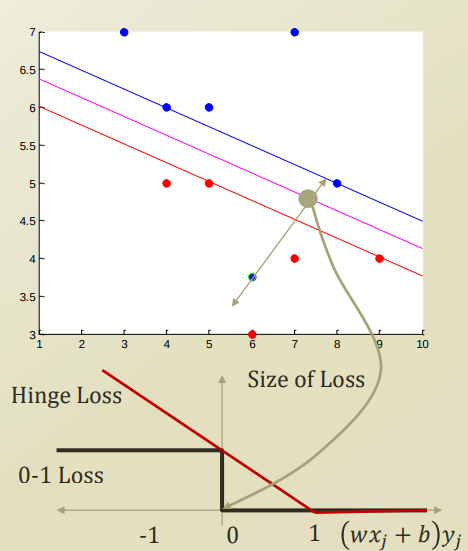
5.3 Soft Margin with SVM

Soft Margin

• Admin there will be an “error”
• Represent the error in our problem formulation
• Try to reduce the error as well

Soft Margin과 Kernel Trick둘다, 위에서 선언한 \(min_{w,b}||w||, s.t(wx_j+b)y_j \ge 1\)로서는 Error를 해결할 수 없으므로 Error에 관한 값을 Penalty Function으로서 나타내고 Penalty Function의 값 또한 Minimize하는 값을 찾아서 Classify하게 한다는 것 이다.

즉, 어느정도 Error는 허용하나 그 Error가 최소화되게 만든다는 의미이다.

Penalty Function을 선언하는 방법은 2가지가 있다.

Option 1

$$min_{w,b}||w||+C*(\text{Num of Error})$$

$$s.t(wx_j+b)y_j \ge 1$$

위의 식을 살펴보게 되면 Error의 개수 * C(임의의 상수)만큼 Penalty를 준다는 것 이다.
이러한 Penalty Function은 0-1 Loss라고 부르게 된다.
0-1 Loss란 Hyperplane까지는 Penalty가 없으나 반대쪽의 Support Vector를 넘어가는 순간 1의 Penalty를 주는 Penalty Function이다. 하지만, 이러한 Function은 거리와 상관없이 Count만으로서 Penalty를 주기 때문에 정확한 방법이라고 할 수 없다.

Option2

$$min_{w,b}||w||+C\sum_{j}\xi_j$$

$$s.t(wx_j+b)y_j \ge 1-\xi_j$$

$$\xi_j =(1-(wx_j+b)y_j)_{+} \rightarrow \xi_j \ge 0$$

위의 식을 살펴보게 되면 \(\xi\)는 Distance에 따라 \(\xi_j\)만큼 Penalty를 주겠다는 의미이다.
0-1 Loss에서의 문제점이였던, 거리에 따른 가중치를 주지 않는 것은 해결하였다. 이러한 Loss Function은 Hinge Loss라고 불린다. 하지만, C라는 Constant를 정의해야 하는 새로운 문제가 발생하게 되었다.

위의 Option1,2의 Penalty Function을 SVM에 적용하여 Visualizatio하면 다음과 같이 나타낼 수 있다.

새로운 Constant C에 대하여 값을 변경시키면서 결과를 출력하면 다음과 같은 결과를 얻을 수 있다.

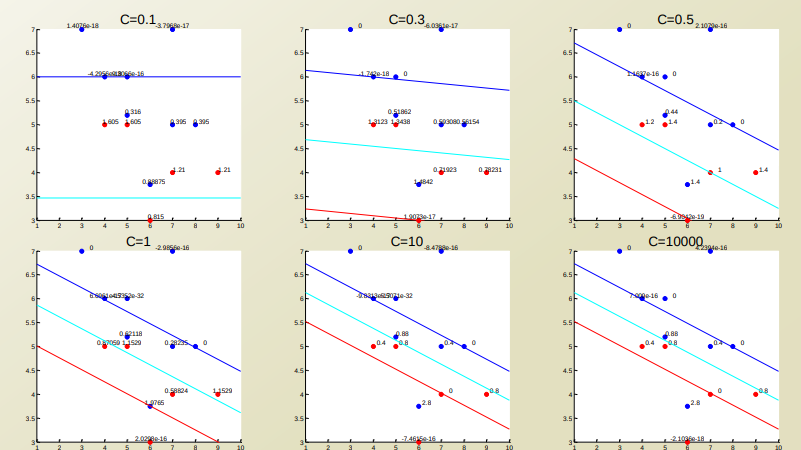
Data가 Linear하게 Classify되지 않는다고 가정하였을 경우, Penalty가 작으면 여전히 잘 분류하지 못하지만, 일정 크기 이상일 경우에는 어느정도의 Error를 감수하고 잘 분류하는 것을 살펴볼 수 있다. 이러한 C의 값은 무조건 크면 좋은 것이 아니라, 우리가 사용하고자 하는 Data의 신뢰도에 따라 Penalty를 줘야지 의미있는 Classification Model(SVM)을 설계할 수 있을 것 이다.

5.4 Comparison to Logistic Regression

위의 SoftMargin SVM에서 LossFunction을 Hinge Loss로서 사용하였다.

이러한 LossFunction은 이전에 배웠던 Logistic Regression에서도 사용하였다.
4.3 Logistic Regression Parameter Approximation 1에서 Logistic Regression식 을 생각해보자.

$$\hat{\theta} = \argmax_{\theta} \sum_{i=1}^N log(P(Y_i|X_i ;\theta)) = \argmax_{\theta}\sum_{i=1}^{N}(Y_iX_i\theta - log(1+e^{X_i\theta}))$$

위의 식을 살펴보게 되면 LossFunction은 \(log(1+e^{X_i\theta})\)가 되는 것을 살펴볼 수 있다.

최종적인 0-1, Hinge, Log Loss는 다음과 같이 나타낸다.

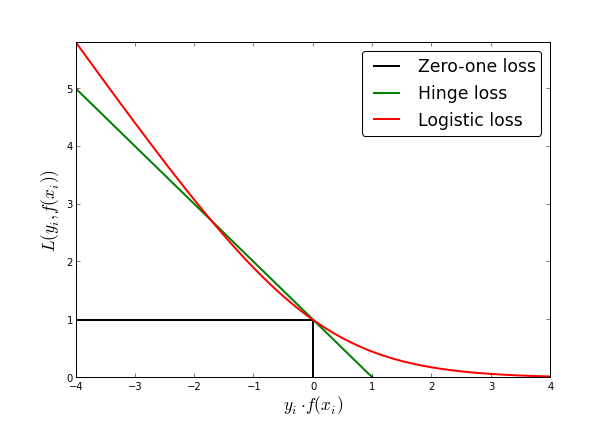
사진 출처: fa.bianp

위의 Loss를 생각해보면 다음과 같은 의미를 가지고 있다.
SVM의 경우 Hyperplane을 기준으로서 Prediction이 맞다면 Penalty가 0이다. 즉, 완벽히 Classification가능하다고 생각한다는 것 이다.

Logistic Regression의 Log Loss Function을 살펴보게 되면, 아주 잘못되어도 0이아닌 값을 가지게 된다.(0에 매우 가까울 것 이다.)즉, 아주 0에 가까운 확률로서 Prediction이 잘못되었다고 판단할 수 있다는 것 이다.