Theory8. K-Means Clustering and Gaussian Mixture Model(2)

8. K-Means Clustering and Gaussian Mixture Model(2)

\(\newcommand{\argmin}{\mathop{\mathrm{argmin}}\limits}\) \(\newcommand{\argmax}{\mathop{\mathrm{argmax}}\limits}\) Machine Learning의 기초적인 이론부분을 다시 제대로 잡고 싶어서 문일철 교수님의 인공지능 및 기계학습 개론을 정리한 Post입니다.

• 8.3 Multinomial Distribution
• 8.4 Mutivariate Gaussian Distribution
• 8.5 Gaussian Mixture Model

8.3 Multinomial Distribution

• Selecting 0 or 1 => Binomial Distribution
• Selecting 0 or 1 or …. or M => Multinomial Distribution

주사위 던지기 예제에 적용하여 생각해 보자.

• x: 선택지 ex) 주사위한번 던졌을 경우 숫자가 나온 개수(0,0,1,0,0,0)
• \(\mu\): 확률 ex) 주사위의 각각의 숫자가 나올 확률

$$\sum_{k}x_k = 1, P(X|\mu) = \prod_{k=1}^{K} \mu_k^{x_k}, \mu_k \ge 0, \sum_{k}\mu_{k}=1$$

위의 식을 살펴보게 되면 Binormial Distribution의 General한 Version인 것을 확인할 수 있다.
주사위의 6가지 경우의 수가 아닌 실제 Dataset에 적용시키면 다음과 같이 식을 변형할 수 있다.

• D: Dataset with N selections => \(x_1, ..., x_n\)

$$P(X|\mu) = \prod_{n=1}^{N} \prod_{k=1}^{K} \mu_k^{x_{nk}} = \prod_{k=1}^{K} \mu_k^{\sum_{n=1}^{N} x_{nk}} = \prod_{k=1}^{K} \mu_k^{m_k}$$

ex) 주사위를 25번 던졌다.

• x: x1, x2, …, x25
• k: 1,2,3,4,5,6
• \(\mu\): 1/6, 1/6, 1/6, 1/6, 1/6, 1/6

MLE of Multinormial Distribution
Multinormial Distribution의 확률을 구할 수 있으므로, 이 확률의 MLE는 다음과 같이 나타낼 수 있다.

$$\text{Maximize} P(X|\mu) = \prod_{k=1}^{K} \mu_{k}^{m_k}$$

$$\text{Subject to} \mu_k \ge 0, \sum_{k} \mu_k = 1$$

어떠한 Function을 Maximize하는데 제약조건이 있으므로 5. SVM과 같이 Largrange Method로서 해결한다.

$$L(\mu, m, \lambda) = \sum_{k}m_k ln(\mu_k) + \lambda(\sum_{k}\mu_k -1)$$

$$\frac{d}{d \mu_k}L(\mu, m, \lambda) = \frac{m_k}{\mu_k} + \lambda =0 \rightarrow \mu_k = -\frac{m_k}{\lambda}$$

$$\sum_{k} \mu_k =1 \rightarrow -\sum_{k}\frac{m_k}{\lambda} = 1 \rightarrow \sum_{k} m_k = -\lambda \rightarrow \sum_{k}\sum_{n}x_{nk} = N$$

$$\therefore -\lambda = N \rightarrow \mu_{k} = \frac{m_k}{N}$$

MLD of Multinormial Distribution은 MLE of Bionomial Distribution(\(\hat{\theta} = \frac{\alpha_H}{\alpha_H+\alpha_T}\))와 형태가 같은 \(\frac{\text{해당 횟수}}{\text{전체 횟수}}\)라는 것을 확인할 수 있다.

8.4 Multivariate Gaussian Distribution

먼저 Gaussian Distribution의 식을 다시한번 생각해보면 다음과 같이 나타낼 수 있다.

$$N(x|\mu,\sigma^2) = \frac{1}{\sqrt{2\pi \sigma^2}}exp(-\frac{1}{2\sigma^2}(x-\mu)^2)$$

위와 같은 식은 \(\mu, \sigma\)가 각각의 1개의 값을 가지는 단순한 Gaussian Distribution이다.

위의 식을 활용하여 Multivariabe Gaussian Distribution을 나타내면 다음과 같이 나타낼 수 있다.

$$N(x|\mu,\boldsymbol{\Sigma}) = \frac{1}{2\pi^{D/2}}\frac{1}{|\boldsymbol{\Sigma}|^{1/2}}exp(-\frac{1}{2}(x-\mu)^T \boldsymbol{\Sigma}^{-1}(x-\mu))$$

\(\mu, \boldsymbol{\Sigma}\)이 더이상 단일 값이 아니라 Dimension의 개수만큼 가져야 하므로, Matrix로서 표현하게 되어서 식이 변하게 되었다.
\(\boldsymbol{\Sigma}\)은 Covariance Matrix로서 표현된다.

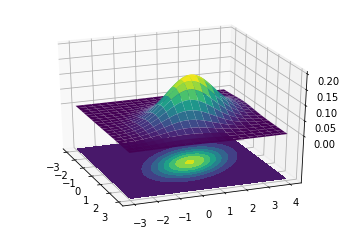
실제 잘 감이 안잡히므로 Multivariate Gaussian Distribution을 Visualization하면 다음과 같다.

import numpy as np
import matplotlib.pyplot as plt
from matplotlib import cm
from mpl_toolkits.mplot3d import Axes3D

# Our 2-dimensional distribution will be over variables X and Y
N = 60
X = np.linspace(-3, 3, N)
Y = np.linspace(-3, 4, N)
X, Y = np.meshgrid(X, Y)

# Mean vector and covariance matrix
mu = np.array([0., 1.])
Sigma = np.array([[ 1. , -0.5], [-0.5,  1.5]])

# Pack X and Y into a single 3-dimensional array
pos = np.empty(X.shape + (2,))
pos[:, :, 0] = X
pos[:, :, 1] = Y

def multivariate_gaussian(pos, mu, Sigma):
    """Return the multivariate Gaussian distribution on array pos.

    pos is an array constructed by packing the meshed arrays of variables
    x_1, x_2, x_3, ..., x_k into its _last_ dimension.

    """

    n = mu.shape[0]
    Sigma_det = np.linalg.det(Sigma)
    Sigma_inv = np.linalg.inv(Sigma)
    N = np.sqrt((2*np.pi)**n * Sigma_det)
    # This einsum call calculates (x-mu)T.Sigma-1.(x-mu) in a vectorized
    # way across all the input variables.
    fac = np.einsum('...k,kl,...l->...', pos-mu, Sigma_inv, pos-mu)

    return np.exp(-fac / 2) / N

# The distribution on the variables X, Y packed into pos.
Z = multivariate_gaussian(pos, mu, Sigma)

# Create a surface plot and projected filled contour plot under it.
fig = plt.figure()
ax = fig.gca(projection='3d')
ax.plot_surface(X, Y, Z, rstride=3, cstride=3, linewidth=1, antialiased=True,
                cmap=cm.viridis)

cset = ax.contourf(X, Y, Z, zdir='z', offset=-0.15, cmap=cm.viridis)

# Adjust the limits, ticks and view angle
ax.set_zlim(-0.15,0.2)
ax.set_zticks(np.linspace(0,0.2,5))
ax.view_init(27, -21)

plt.show()

Mixture Model
이러한 Gaussian Mixture Model을 사용해야 하는 이유를 생각하면 다음과 같다.
현재 다음과 같은 Data Distribution이 있다고 하자.

위와 같은 상황인 경우 Gaussian Distribution으로서 Data Distribution을 예측하면 다음과 같다.

잘 Fitting이 되지 않는다고 할 수 있다.
즉, Multivariabe Gaussian Distribution로서 여러개의 평균과 분산으로서 Gaussian Distribution여러개를 사용하여 Data Distribution을 Prediction하면 다음과 같은 형태가 된다.

위와 같은 이유로서 GMM(Gaussian Mixture Model)을 사용하는 것 이다.

이러한 GMM을 식으로서 표현하면 다음과 같다.

$$P(x) = \sum_{k=1}^{K} \pi_{k} N(x|\mu_k,\sigma_k)$$

$$\sum_{k=1}^{K}\pi_k =1, 0 \le \pi_k \le 1$$

중요하게 봐야하는 점은 \(\pi_k\)은 K개의 Gaussian Distribution에서 각각의 Gaussian Distribution의 속할 확률로서 0~1 사이의 값을 가지게 된다. 이는 K-Means의 Hard Clustering(Cluster에 속하냐 안하냐로서만 표현- 0 or 1)이 아닌, Soft Clustering으로서 표현된다는 것 이다.

참조(Covariance Matrix)
Covariance Matrix는 정말 많이 사용되는 Matrix의 종류 중 하나이므로 꼭 이해하고 넘어가야 한다.

각각의 Element에 관하여 Covariance 관계를 나타낸 Matrix이고 수학적인 수식으로 나타내면 다음과 같다.

위의 Covariance Matrix에서 주요하게 봐야하는 점은 4가지 이다.

1. Covariance Matrix는 Symmentric Matrix 이다.
2. Covariane Matrix의 Diagonal은 각각의 Element의 Variance을 의미한다.
3. Covariance Matrix의 Diagonal을 제외한 각각의 Element는 두개의 Element끼리의 Covariance를 의미한다.

Covariance Matrix를 좀 직관적으로 살피기 위하여 2차원이라고 한정하고 몇개의 예시를 살펴보면 다음과 같다.

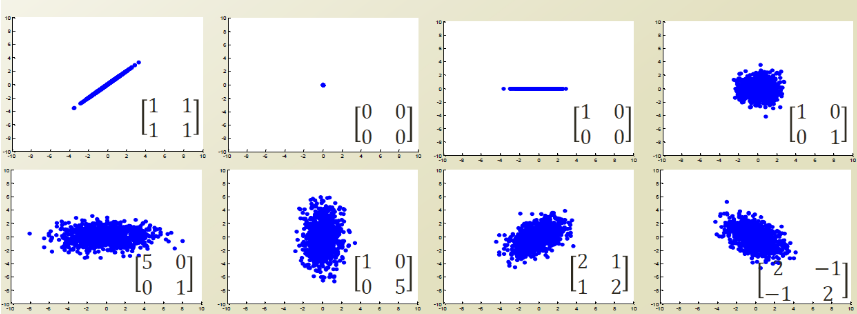
위의 그림을 왼쪽 위부터 살펴보면 다음과 같다.

1. Varaince와 Covariance가 각각 1이다. 즉, x축으로의 분산, y축으로의 분산이 각각 1이고, Correlation값을 계산항여도 1이니, y=x와 같은 형태로서 나타내게 된다.
2. Variance와 Covariance가 각각 0 이다. 즉, x축,y축으로의 분산이 없는 상태이므로 하나의 Point로서 나오게 된다.
3. x축으로만 분산이 있는 상황이다. 즉, 2차원에서 x축으로만 값이 존재하는 형태로서 표현된다.
4. x,y축으로의 분산만 존재하는 상황이다. Covariance가 0이므로 원의 형태로서 나오게 된다.
5. x축의 분산이 y축의 분산보다 큰 상황이다. 즉 타원형태이지만 x축의 길이가 더 길다.
6. 5와 형태가 같다.
7. 1의 형태에서 분산만 두배로 커진다.
8. 7의 형태에서 Covariance의 부호만 바뀌게 된다. => Correlation의 방향이 반대이다.

위와 같은 Covariance의 특징을 통하여 SVD, PCA에서도 사용하게 된다.
이전 Post SVD의 식을 살펴보면 다음과 같다.

$$A = U \sum V^{T}$$

위의 식을 다시한번 생각해보게 되면, Orthogonal Matrix(U,V)로서 회전변환 하여 Covariance Matrix에서 Diagonal형태가 되도록 EigenVector를 설정한다. Eigen Vector에서 값이 적은 축을 제거 한다. => 위의 예시에서 3번인 경우 y축 제거

위와 같은 PCA를 그림으로 살펴보면 다음과 같다.

사진 참조: https://medium.com/mighty-data-science-bootcamp/unsupervised-learning-pca-k-means-a95aa72bf27f

8.5 Gaussian Mixture Model

$$P(x) = \sum_{k=1}^{K} \pi_{k} N(x|\mu_k,\sigma_k) = \sum_{k=1}^{K}P(z_k)P(x|z)$$

$$\sum_{k=1}^{K}\pi_k =1, 0 \le \pi_k \le 1$$

• \(\pi_{k} = P(z_k)\): 어떤 Cluster를 선택할 것 인가. Mixing Coefficient
• \(N(x|\mu_k,\sigma_k)=P(x|z)\): Cluster의 Gaussian Distribution Mixture Component

Example) 실제 Data x가 들어왔을 때 어떤 Cluster에 Assign될 것인가?

$$\gamma(z_{nk}) = P(z_k=1|x_n) = \frac{P(z_k=1)P(x|z_k=1)}{\sum_{j=1}^{K}P(z_j=1)P(x|z_j = 1)}= \frac{\pi_k N(x|\mu_k,\boldsymbol{\Sigma}_k)}{\sum_{j=1}^{K}\pi_j N(x|\mu_j \boldsymbol{\Sigma}_j)}$$

위의 식은 매우 간단하다.
MLE of Multiormial Distribution와 같이 \(\frac{해당 Cluser에 속할 확률}{전체 Cluster에 속할 확률}\)로서 표현하게 된다.

위의 식(Gaussian Mixture Model)을 Log Likelihood로서 표현하면 다음과 같이 나타낼 수 있다.

$$ln(P(X|\pi,\mu,\boldsymbol{\Sigma})) = \sum_{n=1}^{N}ln[\sum_{k=1}^{K} \pi_k N(x|\mu_k,\boldsymbol{\Sigma}_k)]$$