Theory9. Hidden Markov Model

9. Hidden Markov Model

\(\newcommand{\argmin}{\mathop{\mathrm{argmin}}\limits}\) \(\newcommand{\argmax}{\mathop{\mathrm{argmax}}\limits}\) 이번 Post는 문일철 교수님의 머신러닝 보다는 실제 Problem에 접목시켜서 Hidden Markov Model에 대하여 알아보고, 실제 Model을 Code로서 확인하는 Post입니다. (많은 책에서 Code는 다루지 않아서 나중에 사용하기 위하여 정리하였습니다.)

• 9.1 What is Hidden Markov Model?
• 9.2 Viterbi Decoding Algorithm
• 9.3 Forward-Backward probability Cacluation
• 9.4 Baum-Welch Algorithm

9.1 What is Hidden Markov Model?

HMM(Hidden Markov Model)이라는 것은 Data를 가지고 Hidden인 State를 측정하는 Algorithm이다.

실제 이러한 설명만으로는 와닿지 않으니 예제로 들면 다음과 같다.
어떠한 Data가 ATCGA… 같은 Data가 관측되었다고 하자.
각각의 Data A or T or C or G는 q0 or q1 or q2 or q3 or q4의 State라고 가정하자.

그렇다면 우리는 X(=ATCGA…)만 Observation하여서 Latent Varialbes인 State를 측정하겠다는 의미이다.

이전 Post 8. K-Means Clustering and Gaussian Mixture Model 와 같이 Latent Variables를 측정해야 하므로 EM Algorithm으로서 해결할 수 있다.

알 수 있는 사실은 State는 Intron, Exon이 존재하게 되고, 각각의 State의 Emission은 A,T,C,G가 있다는 것 이다.

앞으로 실제 접근할 Example을 살펴보면 다음과 같다.

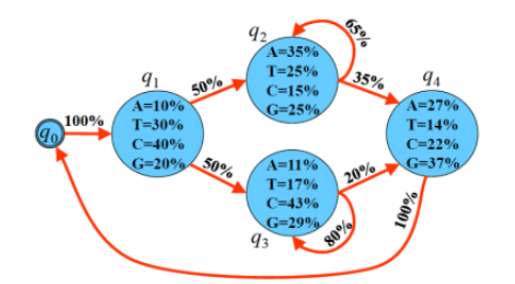
위의 문제에 맞게 앞으로의 식에서 공통으로 사용할 Notation을 정리하면 다음과 같다.

• 𝐴=\(a_{ij}\): i 번째 State에서 j번째 State로 넘어갈 확률 => Transition Probability
• 𝐵=\(b_i(o_t)\): i 번째 State에서 𝑜𝑡가 Emission될 확률 => Emission Probability
• 𝑂=[𝐴,𝑇,𝐶,𝐺,𝑇,𝐴]: 관측된 Data -> Length: 6
• 𝑄=[𝑞0,𝑞1,𝑞2,𝑞3,𝑞4]: 나타낼 수 있는 Status

모든 확률은 Conditional로서 나타낼 수 있다.
즉, 생각해보면 각각의 A,B를 다음과 같이 생각할 수 있다.

• \(a_{ij} = P(j|i)\): 현재 i State일때 다음 State가 j일 확률
• \(b_i(o_t) = P(o|i)\): 현재 i State일때 o를 Emission할 확률

즉, Conditional Probability로서 모든 것을 표현할 수 있다는 것 이다.

9.2 Viterbi Decoding Algorithm

먼저 최종적인 Viterbi Algorithm을 살펴보면 Notation은 다음과 같이 정리 된다.

• \(𝑉_t(𝑗)=max_i[𝑉_t−1(𝑖)𝑎_{ij}𝑏_j]\): Viterbi Algorithm => t번째 시점에서 j번째 은닉 상태가 관측되고 관측치 𝑂𝑡(=A or T or C or G) 가 관측될 확률
• j=0: A
• j=1: T
• j=2: C
• j=3: G
• \(b_t(j)= \argmax_i[V_{t−1}(𝑖)∗a_{ij}∗b_j(o_t)]\): Traceback => 확률이 높은 Status를 계산하기 위한 Traceback

현재 실제 Data는 ATCGTA가 관측되었다. 각각의 State로 넘어갈 확률이랑, 각각의 State에서 Emission될 확률이 존재하므로, 이러한 Sequence가 나올 수 있는 모든 경로를 생각하면 다음과 같이 나타낼 수 있다.(갈 수 없는 곳은 제외한다.)

Viterbi Algorithm값을 생각해보면, i->j가 될수 있는 모든 Transmission Probability와 i번째의 각각의 State에서 Emission될 Probability의 곱 중 가장 큰 값을 선택하게 된다. 따라서 가장 높을 확률을 선택하게 되면, Data Sequence에 맞는 확률이 높은 State를 찾아낼 수 있다.

Traceback을 살펴보게 되면, Viterbi Algorithm은 MAX값을 선택하므로 그 값을 어디에다가 저장해두면, Argmax를 통하여 가장 확률이 높은 곳으로서 Traceback이 가능하다는 것 이다.

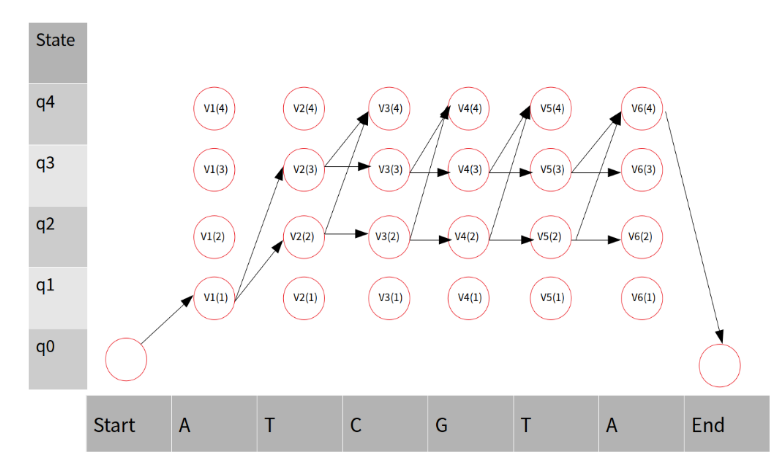
위의 그림을 Matrix로서 표현하기 위하여 각각의 𝑉𝑖(𝑗)를 계산하게 되면 다음과 같이 나타낼 수 있습니다. (Viterbi Algorithm식은 Max를 사용하여야 하나, q2를 예시로 하면, q1 -> q2는 처음만 가능하고, q1 -> q2, q3 -> q2, q4 -> q2는 불가능 합니다. 마찬가지로 q3도 적용할 수 있습니다. 따라서 max로서 값을 표현하는 것이 아닌 경우의 수가 하나만 가능한 상태로 식을 사용하였습니다.)

𝑉1(1) = 𝑎01∗𝑏0(0) =1∗0.1=0.1

𝑉2(2)=𝑉1(1)∗𝑎12∗𝑏2(1)=0.1∗0.5∗0.25=0.0125 𝑉2(3)=𝑉1(1)∗𝑎13∗𝑏3(1)=0.1∗0.5∗0.17=0.0085

𝑉3(2)=𝑉2(2)∗𝑎22∗𝑏2(2)=0.0125∗0.65∗0.15=0.00121875 𝑉3(3)=𝑉2(3)∗𝑎33∗𝑏3(2)=0.0085∗0.8∗0.43=0.002924 𝑉3(4)=𝑚𝑎𝑥[0,𝑉2(2)∗𝑎24∗𝑏4(2),𝑉2(3)∗𝑎34∗𝑏4(2),0] =𝑚𝑎𝑥[0,0.0009625,0.000374,0]=0.0009625 𝑉4(2)=𝑉3(2)∗𝑎22∗𝑏(3)=0.00121875∗0.65∗0.25=0.000198047 𝑉4(3)=𝑉3(3)∗𝑎33∗𝑏3(3)=0.002924∗0.8∗0.29=0.000678368 𝑉4(4)=𝑚𝑎𝑥[0,𝑉3(2)∗𝑎24∗𝑏4(3),𝑉3(3)∗𝑎34∗𝑏4(3),0] =𝑚𝑎𝑥[0,0.000157828,0.000216376,0]=0.000216376

𝑉5(2)=𝑉4(2)∗𝑎22∗𝑏2(1)=0.000198047∗0.65∗0.25=0.000032183 𝑉5(3)=𝑉4(3)∗𝑎33∗𝑏3(1)=0.000678368∗0.8∗0.17=0.000092258 𝑉5(4)=𝑚𝑎𝑥[0,𝑉4(2)∗𝑎24∗𝑏4(1),𝑉4(3)∗𝑎34∗𝑏4(1),0] =𝑚𝑎𝑥[0,0.00009704,0.000018997,0]=0.000018997

𝑉6(2)=𝑉5(2)∗𝑎22∗𝑏2(0)=0.000032183∗0.65∗0.35=0.000007322 𝑉6(3)=𝑉5(3)∗𝑎33∗𝑏3(0)=0.000092258∗0.8∗0.11=0.000008119 𝑉6(4)=𝑚𝑎𝑥[0,𝑉5(2)∗𝑎24∗𝑏4(0),𝑉5(3)∗𝑎34∗𝑏4(0),0] =𝑚𝑎𝑥[0,0.000003481,0.000004982,0]=0.000004982

실제 계산한 값을 Matrix로서 표현하면 다음과 같다.

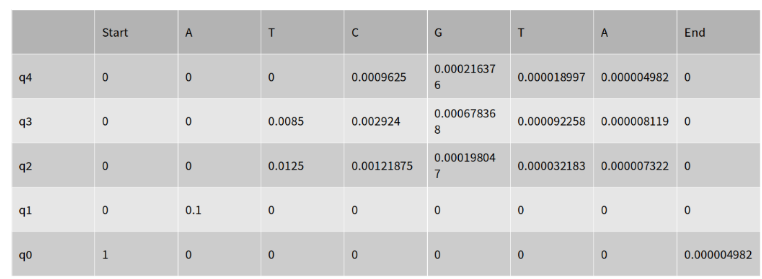
Trace Back을 수행한 결과는 다음과 같다.

• End: 𝑎𝑟𝑔𝑚𝑎𝑥[0,0,0,1∗.000004982]=3=𝑞4
• End-1: 𝑎𝑟𝑔𝑚𝑎𝑥[0,0.000003481,0.000004982,0]=q2

• End-2: 𝑎𝑟𝑔𝑚𝑎𝑥[0,0,0.000092258,0]=2=𝑞3

  …

• Start + 1: 𝑎𝑟𝑔𝑚𝑎𝑥[0.1,0,0,0]=0=𝑞1

따라서 Traceback의 결과로 인하여 State가 변한 과정은 다음과 같이 나타낼 수 있다. 𝑞0→𝑞1→𝑞3→𝑞3→𝑞3→𝑞3→𝑞4→𝑞0

위의 과정을 Matrix에 연관지어 생각하면 다음과 같이 표시할 수 있다.

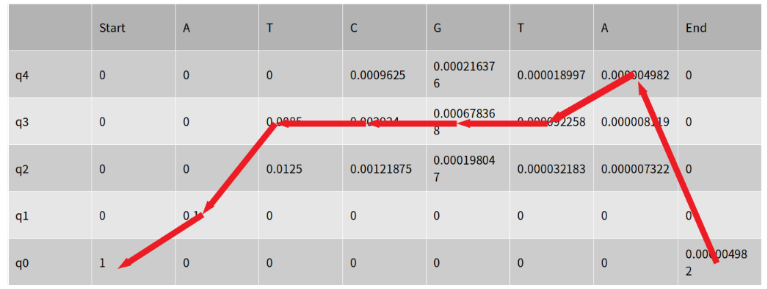
9.3 Forward-Backward probability Cacluation

Hidden Markov Model의 전반적인 내용과 State를 알아낼 수 있는 Viterbi Algorithm의 경우에는 간단하므로 실제 Data에 적용을 하여 알아보았다.

Forward-Backward와 Baum-Welch Algorithm의 경우에는 Model을 실질적으로 Trainning하는 부분이므로 좀 더 Genearl한 상태의 수식을 유도해가며 알아보자. (이전에 사용한 Notation은 그대로 사용합니다.)

각각의 Forward, Backward Probability는 다음과 같이 표시합니다.

• Forward Probability: \(\alpha_t(j) = \sum_{i=1}^{n} \alpha_{t-1}a_{ij}b_j(o_t)\)
• Backward Probability: \(\beta_t(i) = \sum_{i=1}^{n} \beta_{t+1}(j)a_{ij}b_j(o_t)\)

Viterbi Algorithm의 식인 \(𝑉_t(𝑗)=max_i[𝑉_t−1(𝑖)𝑎_{ij}𝑏_j]\)와 비교하게 되면, Viterbi Algorithm은 Max값을 찾으므로 Indexing을 통하여 TraceBack이 가능하였다면, Forward-Backward Probability는 모든 확률을 Summation하는 것이기 때문에 TraceBack이 불가능 하다. 하지만, Summation이므로 이를 활용하여 각각의 확률에 대하여 Update가 가능하다.

최종적으로 Model을 사용하게 되면(9-5 Code) Forward-Backward Probability를 사용한 Baum-Welch Algorithm으로서 Update를 하게 되고, Viterbi Algorithm으로서 Model을 평가하게 된다.

전방확률(Forward Probability)의 예시를 살펴보면 다음과 같습니다.
사진 참조: ratsgo 블로그

$${ \alpha }_{ 3 }(4)=\sum _{ i=1 }^{ 4 }{ { \alpha }_{ 2 }(i)\times { a }_{ i4 } } \times { b }_{ 4 }({ o }_{ 3 })$$

후방확률(Backward Probability)의 예시를 살펴보면 다음과 같습니다.
사진 참조: ratsgo 블로그

$${ \beta }_{ 3 }(4)=\sum _{ j=1 }^{ 4 }{ { a }_{ 4j } } \times { b }_{ j }({ o }_{ 4 })\times { \beta }_{ 4 }(j)$$

이 두확률을 곱하면 특정 Node를 지나는 모든 Probability를 얻을 수 있다는 것을 알 수 있다.

사진으로서 표현하면 다음과 같습니다.

사진 참조: ratsgo 블로그

$${ \alpha }_{ t }\left( j \right) \times { \beta }_{ t }\left( j \right) =P\left( { q }_{ t }=j,O|\theta \right)$$

위의 수식을 활용하면 HMM의 모든 확률에 대해서 구할 수 있다.(Start State는 q0라고 생각한다면)

$$P(O|\theta) = \sum_{i=1}^{n} \alpha_t(s)\beta_t(s) = P(q_t=q_0,O | \theta) = \beta_o(q_0)$$

9.4 Baum-Welch Algorithm

우리는 위에서 \({ \alpha }_{ t }\left( j \right) \times { \beta }_{ t }\left( j \right) =P\left( { q }_{ t }=j,O|\theta \right)\)식을 얻었다.

잘 생각해보녀 Baum-Welch Algorithm은 EM Algorithm이다.
Latente Variable인 State를 측정하기 위하여 Forward, Backward 값을 계산하는 단계가 E-Step이고 이러한 값을 활용하여 A,B,Initial Probability를 Update하기 때문이다.

M-Step
1. Emission Probability
특정 t시점에서 Observation이 j일 확률은 매우 계산하기 쉽다.

$$\gamma_t(j) = P\left( { q }_{ t }=j|O,\theta \right)$$

$$= \frac{P\left( { q }_{ t }=j,O|\theta \right)}{P(O|\theta)} = \frac{\alpha_{t}\left( j \right) \times \beta_{ t }\left( j \right)}{\sum_{i=1}^{n} \alpha_t(s)\beta_t(s)}$$

위에서 미리 구한 식으로서 편하게 나타낼 수 있기 때문이다.

위의 식을 활용하여 실제 Emission Probability를 Update하면 다음과 같이 나타낼 수 있다.

$$\hat{b_j}(v_k) = \frac{\sum_{t=1, s.t.o_t=v_k}^{T}\gamma_t(j)}{\sum_{t=1}^{T}\gamma_t(j)}$$

위의 식을 살펴보게 되면, 모든 Observation에서 Emission Probability를 계산한 값과 Model이 예측한 Observation이 실제 Observation이 같은 때의 확률로서 나타내게 된다.

2. Transmission Probability
Transmission인 경우에는 한가지 더 생각해야 하는 점이 있다. 특정 시점에서의 Emission이 ${ q }_{ t }=i$인 경우에 ${ q }_{ t +1}=j$이 되어야 하기 때문에다. 즉, 현재 측정하고자하는 t시점에서 다음 시점까지 생각해야 하기 때문이다.

따라서 위에서 구한 식에서 \(a_{ij}b_{j}(o_t)\)를 곱해주어야 한다는 것 이다. 이를 식으로서 나타내면 다음과 같다.

$$% <![CDATA[ \begin{align*} { \xi }_{ t }\left( i,j \right) =&\frac { P\left( { q }_{ t }=i,{ q }_{ t+1 }=j,O|\lambda \right) }{ P\left( O|\lambda \right) } \\ =&\frac { { \alpha }_{ t }\times { a }_{ ij }\times { b }_{ j }\left( { o }_{ t+1 } \right) \times { \beta }_{ t+1 }\left( j \right) }{ \sum _{ s=1 }^{ n }{ \alpha _{ t }\left( s \right) \times \beta _{ t }\left( s \right) } } \end{align*} %]]>$$

위의 수식을 활용하여 Transmission Probability를 Update하면 다음과 같이 나타낼 수 있다.

$$\hat { a } _{ ij }=\frac { \sum _{ t=1 }^{ T-1 }{ { \xi }_{ t }\left( i,j \right) } }{ \sum _{ t=1 }^{ T-1 }{ \sum _{ k=1 }^{ N }{ { \xi }_{ t }\left( i,k \right) } } }$$

위의 식을 살펴보게 되면 i시점에서 j번째 시점으로 갈 수 있는 모든 Transimission Probability에서 실제 확률로서 간 Transmission Probability의 확률로서 나타낸 것을 확인할 수 있다.

위의 두가지에 대한 모든 자세한 수식은 EM-Algorithm을 사용하고, 문일철 교수님 강의에서 자세한 유도를 살펴볼 수 있습니다.