R-ANOVA검정,상관관계분석
ANOVA 검정
3개 이상의 요인 검정 방법
독립변수: 범주형, 종속변수: 연속형
ANOVA 검정이란 통계학에서 두 개 이상 다수의 집단을 비교하고자 할 때 집단 내의 분산, 총평균과 각 집단의 평균의 차이에 의해 생긴 집단 간 분산의 비교를 통해 만들어진 F분포를 이용하여 가설검정을 하는 방법이다.
참조:위키백과
이번 코드에서는 이상치를 제거한다.
이상치: 정상범주에서 크게 벗어난 값. 이상치가 포함되어있을 시, 분석 결과가 왜곡되므로 분석 전에 이상치 제거 작업 필요
| 귀무가설 | 3가지 교육방법을 통한 실기시험 평균의 차이가 없다. |
| 대립가설 | 3가지 교육방법을 통한 실기시험 평균의 차이가 있다. |
| 결과 | p-value(=0.4777 , 0.7012) > 0.05(95% 신뢰확률에서의 유의수준) => 대립가설 채택 |
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
#ANOVA검정
#3가지 교육방법을 적용하여 1개월동안 교육받은 교육생을 대상으로 실기시험을 실시하였다.
#실기시험의 평균에 차이가 있는지 검정
#귀무: 3가지 교육방법을 통한 실기시험 평균의 차이가 없다.
#대립: 3가지 교육방법을 통한 실기시험 평균의 차이가 있다.
data<-read.csv("C:/git/R/Data/three_sample.csv",header = T)
head(data)
#na행 제거
data2<-subset(data,!is.na(score),c("method","score"))
head(data2)
#이상치 제거
plot(data$score)
boxplot(data$score)
length(data$score)
data2<-subset(data,score<=15)
length(data2$score)
boxplot(data2$score)
table(data2$method)
data2$method2[data2$method==1]<-"방법1"
data2$method2[data2$method==2]<-"방법2"
data2$method2[data2$method==3]<-"방법3"
table(data2$method2)
x<-table(data2$method2)
x
y<-tapply(data2$score,data2$method2,mean)
y
df<-data.frame(교육방법=x,성적=y)
df
#정규성 검정
shapiro.test(data2$score) #p-value = 0.1897 > 0.05 -> 정규분포를 따른다.
#등분산성 - 세 집단 간의 동질성 확인
bartlett.test(score~method2,data=data2) #p-value = 0.1905 > 0.05 -> 등분산성OK
#두 집단일때는 var.test 사용
#세 집단 이상일 때는 bartlett.test 사용
install.packages("lattice")
library(lattice)
densityplot(score~(method),data = data2) #1,2,3에 대해서 분산의 차이를 보여준다.
#ANOVA검정
#방법1: aov()
result<-aov(score~method2,data = data2)
result
summary(result) #p-val=0.701
#방법2: anova()
lmodel<-lm(score~method2,data = data2)
anova(lmodel) #p-val=0.7012
#방법3: oneway.test()
oneway.test(score~method2,data = data2) #p-value = 0.4777
oneway.test(score~method2,data = data2,var.equal = T) #p-value = 0.7012
출력결과-방법1

출력결과-방법2
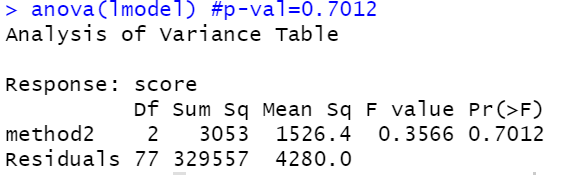
출력결과-방법3

상관관계분석
상관관계분석(correlation analysis)의 기본적인 목적은 변수간의 관계성을 파악하는 것이다. 예를 들어, 국어점수와 산수점수간의 관계성이 어떠한가를 알고자 할 때 대표적으로 상관관계분석을 수행하게 된다.
ANOVA가 변수간의 인과성을 검증하는 대표적인 방법이라면, 상관은 변수간의 관계성만을 파악하는 방법이다. 따라서 상관관계분석에서는 ‘국어점수는 원인변수이고 산수점수는 결과변수이다. 혹은 그 반대이다’와 같이 진술할 수 없다.
변수의 관계성 정도는 관계성의 ‘강도’라 할 수 있다. 보통 상관은 상관계수(correlation coefficient: r)로 표시되는데, 상관계수 r이 크다는 것은 두 변수가 강한 관계성을 가지고 있다는 의미이다.
출처:ABRUPTLY 블로그
1
2
3
4
5
6
#상관관계 분석
result <- read.csv("C:/git/R/Data/drinking_water.csv",header = T,fileEncoding ="UTF-8")
head(result)
summary(result)
cor(result)
cor(result,method="pearson")
출력결과
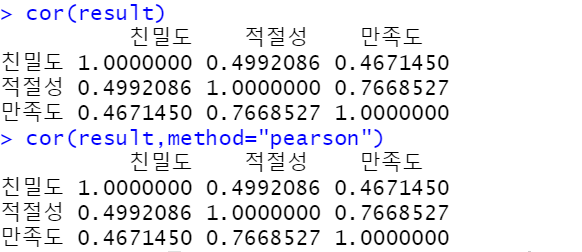
상관관계분석 시각화
1
2
3
4
#상관관계분석 시각화
install.packages("corrgram")
library(corrgram)
corrgram(result)
출력결과
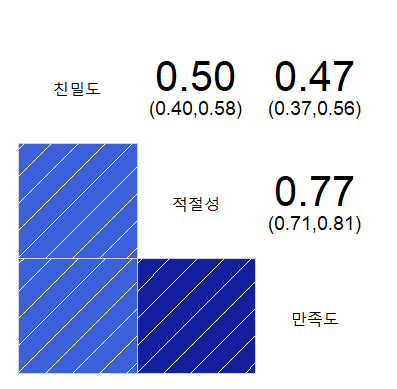
참조: 원본코드
코드에 문제가 있거나 궁금한 점이 있으면 wjddyd66@naver.com으로 Mail을 남겨주세요.

Leave a comment