R-T검정

T검정

T검정이란 두 집간 단의 평균을 비교하는 방법이다. 즉, 두 모집단의 평균의 차이유무를 판단하는 통계적 검정방법으로 단순히 차이의 존재여부를 떠나 그 정도의 통계적 유의미성까지 검정하는 방법

독립변수: 범주형, 종속변수: 연속형
전제조건: 정규분포를 따라야 한다, 일반적으로 표본의 수가 대략 30개 이하일 때 실시

1. One Sample T-검정: 두 집단의 수가 틀려도 상관이 없으며 동일 시점에서 두 집단의 평균을 비교하는 것이다.
2. 동일성 검정: 두 집단의 분포가 동일한가? 다른 분포인가?
3. Independent Sample T-검정: 독립인 두 Sample을 검정할 때 사용 => 등분산성 확인 해야 한다.
4. Paired Sample T-검정: 동일 집단의 전/후의 평균을 비교하는 것으로 전과 후의 수가 동일해야 한다.

T검정 기본 이해

귀무가설	정규분포를 따른다
대립가설	정규분포를 따르지 않는다.
결과	p-value(0.8963) > 0.05(95% 신뢰확률에서의 유의수준) => 귀무가설 채택

#간단한 T 검정
n<-30
mu<-0

set.seed(0)
(x=rnorm(n,mean=mu))
shapiro.test(x) #정규성 확인(p>0.05일시, 정규분포를 따른다.)
stats::t.test(x) #T-검정
wilcox.test(x) #정규성 가정을 충족하지 못하는 경우 or 분포형태를 모르는 경우 wilcox 사용

출력결과-정규셩 확인

출력결과-T 검정

출력결과-Wilcox 검정

One-Sample T-test

귀무가설	여아 신생아의 평균 몸무게는 2800g이다.
대립가설	여아 신생아의 평균 몸무게는 2800g이 아니다.(초과 혹은 미만)
결과	p-value(0.01963) < 0.05(95% 신뢰확률에서의 유의수준) =>귀무가설 기각, 대립가설 채택

# one sample T-test
# 여아 신생아의 몸무게 평균(2800g) 검정
data<-read.csv("C:/git/R/Data/babyboom.csv",header = T)
head(data)

# 귀무가설: 여아 신생아의 평균 몸무게는 2800g이다.
# 대립가설: 여아 신생아의 평균 몸무게는 2800g을 초과한다.
str(data)
(tmp<-subset(data,gender==1)) #여아 데이터 추출
tmp
(weight<-tmp[[3]])
typeof(weight)
nrow(tmp)

#수식을 사용
avg<-mean(weight)
avg
s_dev<-sd(weight)
s_dev
n<-length(weight)
n
h0<-2800
(t_value<-(avg-h0)/(s_dev/sqrt(n))) #t=2.233188

alpha<-0.05 #단측 검정
(c.u<-qt(1-alpha,df=n-1)) #qt(신뢰계수,자유도), 임계값=1.739607
(p.value<-1-pt(t_value,df=n-1)) #p-value<-1-pt(tvalue,df)
# p값:0.01963422<0.05 귀무가설 기각

#방법2: t.test()로 판정
t.test(weight,mu=2800,alternative = "greater")
#t = 2.2332, df = 17, p-value = 0.01963, 귀무가설 기각
#해설: 귀무가설 기각하고 대립가설을 채택한다.
#대립가설: 여아 신생아의 평균 몸무게는 2800g을 초과한다.

출력결과

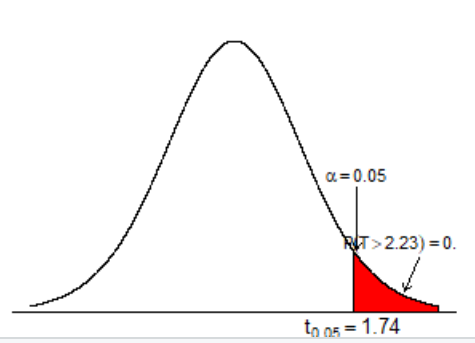
One-Sample T-test 시각화

# one sample t-test 시각화
par(mar=c(0,1,1,1))
x <- seq(-3, 3, by = 0.001)
y <- dt(x, df = n - 1)
plot(x, y, type="l", axes=F, ylim=c(-0.02, 0.38))
abline(h=0)

polygon(c(c.u, x[x > c.u], 3), c(0, y[x > c.u], 0), col=2)
text(c.u, -0.02, expression(t[0.05]==1.74))
text(1.8, 0.2, expression(alpha==0.05), cex=0.8)
arrows(1.8, 0.18, 1.8, 0.09, length=0.05)

polygon(c(t_value, x[x > t.t], 3), c(0, y[x > t.t], 0), density=20, angle = 45)
text(t.t, -0.02, paste("t=", round(t.t, 3)), pos=4)
text(2.65, 0.1, expression(plain(P)(T > 2.23)==0.019), cex=0.8)
arrows(2.7, 0.08, 2.5, 0.03, length=0.05)

출력결과

동일성 검정

귀무가설	국내에서 생산된 노트북과 A사에서 생산된 노트북 평균 사용시간에 차이가 있다.
대립가설	국내에서 생산된 노트북과 A사에서 생산된 노트북 평균 사용시간에 차이가 없다
결과	p-value(0.0001417) < 0.05(95% 신뢰확률에서의 유의수준) =>귀무가설 기각, 대립가설 채택

#동일성 검정
data<-read.csv("C:/git/R/Data/one_sample.csv",header=T)
head(data,3)
x<-data$time #노트북 평균사용시간
summary(x)
mean(x)
x1<-na.omit(x) #NA값은 제외
mean(x1) #NA값(결측치)은 제외한 채로 평균 도출=5.556881

shapiro.test(x1) #p-value = 0.7242 > 0.05 -> 정규분포를 따른다
t.test(x1,mu=5.2) #p-value = 0.0001417 < 0.05

출력결과

Independent Sample T-test

귀무가설	남여 신생아의 몸무게 평균은 차이가 없다.
대립가설	여 신생아의 몸무게는 남 신생아의 몸무게 평균보다 적다.
결과	p-value(0.07526>0.05) > 0.05(95% 신뢰확률에서의 유의수준) => 귀무가설 채택

두 집단이 Independent하면 등분산성 확인
등분산성: 분산분석을 통해 서로 다른 두 개 이상의 집단을 비교하고자 할때, 기본적으로 해당 집단들이 만족해야되는 조건 중 한가지로 분산이 같음을 의미한다.

#서로 독립인 두 집단의 평균차이 검정(Independent Sample T-test)
#남여 신생아의 몸무게 평균차이 검정수행
babydata<-read.csv("C:/git/R/Data/babyboom.csv",header = T)
head(babydata,3)
(data<-babydata[,c("gender","weight")])

var.test(data$weight~data$gender) #등분산성 확인, p-value=0.07526>0.05
t.test(data$weight~data$gender,mu=0,alternative = "less",var.equal = T)
# p-value = 0.06764 > 0.05 귀무가설 채택
qt(0.05,df=42) #임계치 -1.681952

length(data$weight[data$gender==1]) #18
mean(data$weight[data$gender==1]) #3132.444
length(data$weight[data$gender==2]) #26
mean(data$weight[data$gender==2]) #3375.308

#해석: p-value = 0.06764 > 0.05 귀무가설 채택
#남여 신생아의 몸무게 평균은 차이가 없다.라는 결론을 얻는다.

출력결과

Paired Sample T-test

귀무가설	광고 전후 선호도 차이가 없다.
대립가설	광고 전후 선호도 차이가 있다.
결과	p-value(0.015670) < 0.05(95% 신뢰확률에서의 유의수준) => 귀무가설 기각, 대립가설 채택

#Paired Sample Test
bf<-c(11,14,18,21,26,28,37,45,48,60)
af<-c(13,15,17,18,19,23,25,28,29,36)

t.test(bf,af,paired = T) 

출력결과

---

참조: 원본코드
코드에 문제가 있거나 궁금한 점이 있으면 wjddyd66@naver.com으로 Mail을 남겨주세요.