GAT

GRAPH ATTENTION NETWORKS

참조 링크

• GRAPH ATTENTION NETWORKS (GRAPH ATTENTION NETWORKS Paper)

Abstract

We present a scalable approach for semi-supervised learning on graph-structured data that is based on an efficient variant of convolutional neural networks which operate directly on graphs. We motivate the choice of our convolutional architecture via a localized first-order approximation of spectral graph convolutions. Our model scales linearly in the number of graph edges and learns hidden layer representations that encode both local graph structure and features of nodes. In a number of experiments on citation networks and on a knowledge graph dataset we demonstrate that our approach outperforms related methods by a significant margin.

해당 논문에서 제시하는 방법은 기존에 사용되던 GCN (convolutional architecture via a localized first-order approximation of spectral graph convolutions)모델에서 Attention 기법을 사용하여 중요한 이웃 Node를 강조하는 법에 대하여 설명한다.

Notation

• \(N\): Number of nodes
• \(F\): Dimension of node (Node Feature)
• \(F^{'}\): Dimension of hidden Layer (Hidden Layer Feature)
• \(W \in \mathbb{R}^{F \times F^{'}}\): Weight (Trainable Parameter)
• \(a \in \mathbb{R}^{2F^{'}}\): For Attention( Trainable Parameter)

Problem of GCN

먼저, 기존의 GCN에서 사용되는 수식을 살펴보게 되면 아래와 같은 수식으로 나타낼 수 있다.

$$H^{(l+1)} = \sigma (\tilde{D}^{-\frac{1}{2}} \tilde{A} \tilde{D}^{-\frac{1}{2}} H^{(l)} W^{(l)}) - (1)$$

해당 수식에서 문제가 되는 점은 크게 2가지 이다.

1. 모든 그래프의 연결관계를 고려하여 계산하므로 Computational Resource가 많이 든다. -> GraphSAGE에서 Sampling을 통하여 해결하였다. (추후 알아볼 내용)
2. Layer가 깊어질 수록 멀리 있는 중요하지 않은 Node들의 정보까지 모두 생각하여 중요한 정보 손실이 일어나는 문제가 발생한다. -> Graph Attention Network로서 해결.
3. Inductive Learning에서는 사용할 수 없다. -> GraphSAGE에서 해결

GCN의 큰 문제점 중 2번째인 문제점의 방법으로서 Self-Attention을 GNN에 적용하는 방법을 제시한 논문이 “GRAPH ATTENTION NETWORKS” 이다. 또한, Transductive, Inductive에 모두 적용할 수 있는 방법 입니다.

먼저, GCN 논문에서 Layer를 깊게 쌓을 수록 Performance 변화를 측정하면 아래의 사진과 같습니다.

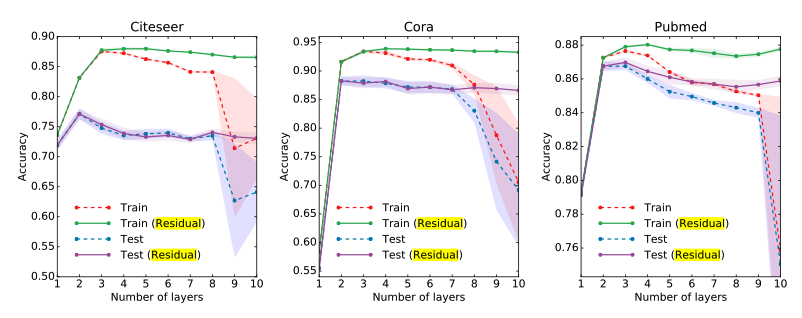
즉, Residual로서 자기 자신의 정보를 계속하여 전달하였을 때, Performance가 유지된다는 실험 결과 입니다. 이와 같이 “Attention”기법은 자기 자신 뿐만 아니라 중요한 정보는 계속해서 강조해서 사용하기 위하여 사용된다.

Graph Attention Network

해당 논문에서의 수식은 아래와 같이 정의된다.

먼저, GNN의 Layer의 Input Data는 아래와 같이 표현된다.

$$\vec{h} = \{\vec{h_1}, \vec{h_2}, \ldots, \vec{h_N} \} \in \mathbb{R}^{N \times F} - (2)$$

위의 수식 (2)에서 GNN으로서 Output (Latent Representation)은 아래와 같이 표현됩니다.

$$\vec{h^{'}} = \{\vec{h^{'}}_1, \vec{h^{'}}_2, \ldots, \vec{h^{'}}_N \} \in \mathbb{R}^{N \times F^{'}} - (3)$$

Self-Attention의 개념을 사용하면, “Output(Query(\(\vec{h}^{'}_i\)))을 계산할때, 주변 Node의 정보 (Key(\(\vec{h}^{'}_j\))) 중에 중요한 정보를 찾아서 사용하자” 입니다.
위의 식을 GCN으로서 나타내면 아래와 같습니다.

$$\vec{h^{'}} = \sigma (\tilde{D}^{-\frac{1}{2}} \tilde{A} \tilde{D}^{-\frac{1}{2}} \vec{h} W)$$

• \(W \in \mathbb{R}^{F^{'} \times F}\): Training Variable

위의 Notation을 활용하여 Attention을 적용하면 아래와 같습니다.

Step 1. Attention Score
Attention Score의 목적은 Query와 참조하고자 하는 Key가 얼만큼 의미가 있나? 입니다.

$$e_{ij} = a(W\vec{h_i}, W\vec{h_j})$$

• \(a \in \mathbb{R}^{2F^{'} \times 1}\): Training Variable

위의 식을 살펴보게 되면, Query와 Key중 한 값을 넣어서 Score를 계산하는 방식이 서로 dot product를 진행하는 것이 아닌 Concat하여 Input으로 사용하고 Training Variable (\(a\))를 곱셈함으로서 나타내었다.

기본적인 Attention 구하는 방식은 다르다. 주의하여서 봐야 할 점은 \(a\)를 공유한다는 것 이다. 즉, 모든 Node간에 서로 영향을 미치는 기준(\(a\))은 학습하여 구하지만, 동일한 기준을 적용하겠다 라는 의미를 가진다.

Appendix. vs NLP: 일반적으로 사용하는 NLP분야에서의 Attention Score와 방법이 다릅니다. NLP 분야에서는 \(W\vec{h_i} \cdot W\vec{h_j}\)으로서 Score를 계산하였습니다. 개인적인 생각으로는 NLP분야에서는 “His name is H.J.Y”인 경우 His와 H.J.Y가 유사하도록 학습하기 위하여 서로 비슷한 Feature를 가졌는지 판단합니다. 이러한 이유는 문법등의 이유가 있습니다. 하지만, Graph에서는 서로 비슷한 Node끼리는 Adjancy Matrix로서 이어져 있기 때문에, 일반적인 Attention Score와 다르게 구하여야 합니다.

Step 2. Attention Distribution
Attention Score를 Softmax취하여 Normalization하는 과정이다.

$$\alpha_{ij} = \text{softmax}_j(e_{ij}) = \frac{exp(e_{ij})}{\sum_{k \in N_i} exp(e_{ik})}$$

Graph의 구조 때문에 조금 변형된 식 입니다. (\(k \in N_i\))조건으로 인하여 주변에 연결된 Node중에서 영향도만을 계산합니다.

해당 저자의 Detail한 부분은 \(\text{softmax}_j\)라고 표시해준 것 이다. 위의 수식의 의미를 생각해보면, “해당 Node i에 영향을 미치는 (연결되어 있는) Node \(N_j\)중에 특정 Node j가 얼만큼 영향을 미치는가?” 이다.

Step 3. Attention Mechanism

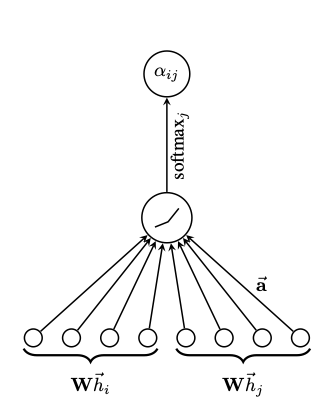
Attention Mechanism이란 위의 그림처럼 논문의 저자들이 하나의 DNN Layer처럼 바꾼 것이며, 위에서 Activation Function (LeakyReLU)를 추가하였다.

$$\alpha_{ij} = \frac{exp( LeakyReLU(e_{ij}))}{\sum_{k \in N_i} exp(LeakyReLU(e_{ik}))}$$

Step 4. Graph Attention Network

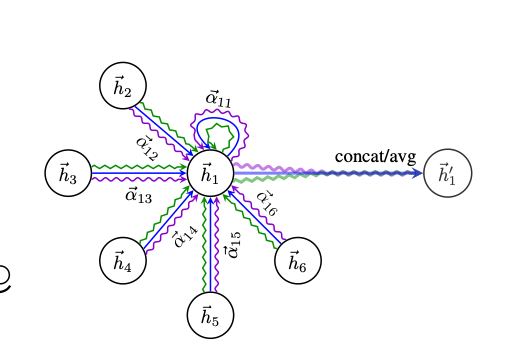
위의 그림은 Graph Attention Network의 최종적인 Figure입니다. 먼저 Self-Attention을 적용한 Output을 적용하면 아래와 같이 적을 수 있습니다.

$$\vec{h^{'}_i} = \sigma(\sum_{j \in N_j} \alpha_{ij} W \vec{h_j})$$

해당 논문에서는 위의 방법이 Stable하지 않다고 말하고 있습니다. 따라서 아래와 같이 Multi-Head Attention을 적용하였다고 말하고 있습니다.

To stabilize the learning process of self-attention, we have found extending our mechanism to em- ploy multi-head attention to be beneficial, similarly to Vaswani et al. (2017). Specifically, K inde- pendent attention mechanisms execute the transformation of Equation 4, and then their features are concatenated, resulting in the following output feature representation:

해당 그림을 수식으로 나타내면 아래와 같습니다. (최종적인 Graph Attention Network)

$$\vec{h^{'}_i} = \sigma(\frac{1}{K} \sum_{k=1}^K \sum_{j \in N_j} \alpha_{ij}^k W^k \vec{h_j})$$

왜 Multi-Head Attention이 의미있는지 생각해보면, 모든 Node에 동일한 적용을 위하여 Share Attention Parameter(\(a\))를 사용한다고 하였습니다. 즉, 하나의 관계밖에 고려할 수 없습니다. 이러한 결과는 두 Hidden Layer Output인 \(\vec{h_i}\)와 \(\vec{h_j}\)간의 Positive or Negative인 하나의 관계밖에 고려할 수 없습니다. 이러한 문제점을 해결하기 위하여 Multi-Head Attention을 사용하게 되면 두 Node간에 다양한 기준으로서 관계성을 파악할 수 있습니다. (Appendix. 해당 논문에서는 K=3으로서 사용하였습니다.)

Result

개인적으로 GNN의 기반의 Model에서 Attention이 필요한 상황은 아래와 같다고 생각한다.

• (1) Node간의 연결된 갯수가 너무 많아서 중요한 Node와의 관계를 고려해야 하는 상황
  • => 해당 문제는 GraphSAGE에서 Node당 연결된 갯수가 Fix되게 Sampling하여 사용 합니다. 따라서, 해당 문제는 Attention말고 GraphSAGE가 더 효과적이라고 생각됩니다.
• (2) Layer를 깊게 쌓고 싶을 때 사용한다.
  • => 해당 문제의 해결점은 Attention으로 밖에 해결할 수 없다고 생각합니다. GNN기반의 Model의 Layer를 쌓을 수록, Node에서 점점 먼 정보를 이용하기 때문에, 어떠한 정보가 중요한지 확인하여야 합니다. 이러한 경우에는 Attention 기법이 중요합니다.

Appendix. Problem of Attention
Graph에 Attention을 적용하는 기법은 최근에 잘 보이지 않고, 문제점이 많다는 의견이 나오고 있습니다. 단점으로 대표되는 문제점은 아래와 같습니다.

• (1) Computation Resource를 많이 잡아먹습니다.
  • => Attention을 계산하기 위한 과정에서 많은 연산과 추가적으로 학습해야 하는 Parameter가 필요합니다.
• (2) 대부분의 GNN을 Modeling할 때, Layer를 깊게 쌓지 않는다고 알려져 있습니다.
  • => 개인적인 생각으로서 “Layer를 깊게 쌓고 Attention을 사용함으로써” 성능이 향상되었다는 것은 Dataset의 문제라고 생각합니다. 즉, 특정 Node의 특성을 정의하기 위해서는 가까운 곳의 Node가 아닌 거리가 먼 곳의 Node의 정보가 필요하다는 의미이다. 이러한 경우는 아래의 2가지의 경우라고 생각됩니다.
    • (1) Adjancy Matrix에서 애초에 잘못 정의되었다고 생각합니다. 이러한 경우에 Clustering으로서 Visualization하여 Node간의 특징을 살펴보아야 할 것 같습니다.
    • (2) Node의 Feature가 매우 Sparse한 경우에 사용해야 할 것 같습니다. Node의 Feature가 대부분의 값이 없다면, 매우 먼 거리까지의 Node정보까지 활용하여 하나의 Group특성을 만들어야 Classification에 활용할 수 있다고 생각합니다.