GraphSAGE

Inductive Representation Learning on Large Graphs

Abstract

Low-dimensional embeddings of nodes in large graphs have proved extremely useful in a variety of prediction tasks, from content recommendation to identifying protein functions. However, most existing approaches require that all nodes in the graph are present during training of the embeddings; these previous approaches are inherently transductive and do not naturally generalize to unseen nodes. Here we present GraphSAGE, a general inductive framework that leverages node feature information (e.g., text attributes) to efficiently generate node embeddings for previously unseen data. Instead of training individual embeddings for each node, we learn a function that generates embeddings by sampling and aggregating features from a node’s local neighborhood. Our algorithm outperforms strong baselines on three inductive node-classification benchmarks: we classify the category of unseen nodes in evolving information graphs based on citation and Reddit post data, and we show that our algorithm generalizes to completely unseen graphs using a multi-graph dataset of protein-protein interactions.

기존에 살펴보았던, GCN이나 다른 GNN의 Model의 가장 큰 문제점은 Transductive Learning 이였다. 즉, Node-Classification수행시 모든 Node에 대한 Edge정보가 필요하다는 것 이다. 하지만, 실제 우리가 사용하는 Dataset은 이러한 상황이 아니다. 즉, 새로운 Sample에 대해서도 Prediction이 가능한 형태여야 한다는 것 이다. 논문저자는 이러한 새로운 Sample에 대해서도 Prediction이 가능한 Inductive Learning형태의 GNN모델인 GraphSAGE(SAmple + aggreGatE)를 제안한다.

Introduction

However, previous works have focused on embedding nodes from a single fixed graph, and many real-world applications require embeddings to be quickly generated for unseen nodes, or entirely new (sub)graphs. This inductive capability is essential for high-throughput, production machine learning systems, which operate on evolving graphs and constantly encounter unseen nodes (e.g., posts on Reddit, users and videos on Youtube). An inductive approach to generating node embeddings also facilitates generalization across graphs with the same form of features

해당 문구는 현재 논문의 가장 큰 Contirubtion을 설명하고 있다. 현재 논문 이전의 모든 GNN기반의 Model을 Transductive Learning으로서 Fixed-Graph 형태로서 이루워져있다. 이러한 Graph의 문제는 새로운 Sample에 대한 Prediction을 할 수 없다는 것 이다.

이러한 문제점을 해결하기 위하여 현재 논문 저자들은 GNN에서 Introduction Learning이 가능한 방법을 제시한다. 제시하는 방법은 Sampling으로서 이루워진다. 이러한 Inductive Learning에서 가장 중요한 것은 “facilitates generalization across graphs with the same form of features”이다.

이러한 Inductive Learning이 Transductive Learning보다 어려운 점은 “Unseen Node”를 “Aligning”하여야 한다는 것 이다. 해당 논문의 저자는 이러한 방법은 아래처럼 제시하였다.

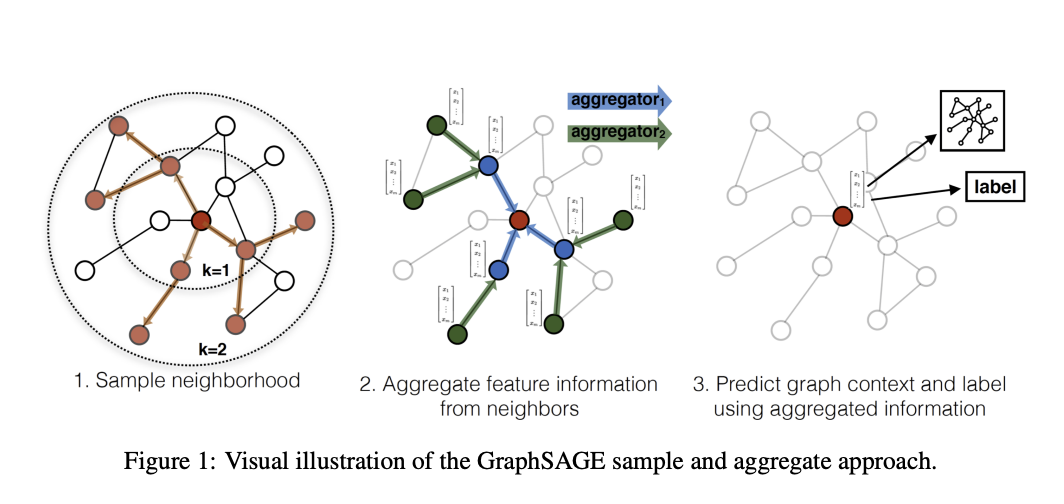
위의 Figure를 살펴보게 되면, 해당 과정은 3과정으로서 이루워 진다. 먼저 “새로운 Sample의 Node는 빨간색 점이라고 가정한다.”

1. 빨간색 점이 어디에 Align할지 기준을 정해야 한다. 이는 빨간색 점을 기준으로 비슷한 점을 Sampling하여 정하게 된다. 즉, Edge정보가 없으므로, 비슷한 점들끼리 이어진다는 가정하에 이러한 과정을 거치게 된다. (해당 논문에서는 이러한 과정을 Embedding이라는 용어로 정의한다.)
2. 주변 정보를 Aggregate한다. 이때, 어느정도멀리 있는 Node간의 정보까지 사용할지 정해야 한다는 문제가 발생하게 된다.
3. 위와 같이 Node를 Align하고, 주변 정보를 활용하여 Latent Representation으로서 표현할 수 있으면, Prediction도 가능하다는 것 이다.

GraphSAGE

Embedding generation algorithm

Notation

• \(\mathbb{g}(V, \xi)\): Graph
• \(x_v, \forall v \in V\): Node
• \(K\): Hop (or Depth, Node기준으로 얼마나 먼 거리까지 생각할 것 인가.)
• \(AGGREGATE_k, \forall k \in \{1, \ldots, K\}\): Aggregator fuction (ex. mean, pooling, LSTM, …)
• \(W^k, \forall k \in \{1, \ldots, K\}\): Weight Matrices
• \(\sigma\): Activation Function
• \(N_k: v \rightarrow 2^V, \forall k \in \{1, \ldots, K\}\): Neightborhood sampling functions
• \(z_v, v \in V\): Vector representation

해당 Section에서는 새로운 Node에 대하여 어떻게 Embedding할지 정하는 과정이다. 주요한 것은 Model은 Training되어 있고, Parameter는 고정되어있다고 가정하고 진행하는 과정이다.

Embedding Generation은 아래와 같이 정의될 수 있다.

해당 Algorithm을 Line by Line으로 생각하면 아래와 같다.

• Line 1: \(h_v^0 \leftarrow x_v, \forall v \in V;\): 모든 Vector에 대하여 생각하겠다.
• Line 2: \(\text{for } k=1, \ldots, K \text{ do}\): 얼만큼 먼 거리까지의 Node (hop=k)를 지정하고 그만큼 반복한다.
• Line 3: \(\text{for }v \in V \text{ do}\): 모든 알고있는 Node에 대하여 진행한다.
• Line 4: \(h_{N(v)}^k \leftarrow AGGREGATE_k (\{ h_{u}^{k-1} \in N(v) \});\): \(h_{N(v)}^k\)는 Input으로 들어온 Node (\(h_v^{k-1}\))와 이어진 Node라고 가정한 Node이다. (Sampling으로서 가정) 이러한 주변 Node의 값을 Aggregate하여 사용한다.
• Line 5: \(h_v^k \leftarrow \sigma(W^k \cdot \text{CONCAT}(h_v^{k-1}, h^k_{N(v)}))\): Input으로 들어온 Node는 이어져 있다는 정의한 Node(\(h_{N(v)}^k\))와 이전 정보 (\(h_v^{k-1}\))를 Concat하여 Weight를 곱하여 나타낸다.
• Line 7: \(h_v^k \leftarrow h^k_v / \| h_v^k\|_2, \forall v \in V\): Normalization하여 사용한다.
• Line 8: \(z_v \leftarrow h_v^K, \forall v \in V\): 예측한 값까지 모두 포함하여 Hidden Representation으로서 표현한다.

위의 Algorithm과정을 살펴보았을 때, 해당 Algirhm을 사용하기 위해서는 2가지가 정의되어야 한다는 것을 알 수 있다.

• 1. 새로운 Node와 이어져 있는 알고있는 Node중에서 어떻게 Sampling할 것 인가? (\(N(v)\))
• 2. Aggregation (\(AGGREGATE_k\))을 어떠한 방법으로 진행할 것 인가?

Relation to the Weisfeiler-Lehman Isomorphism Test

먼저 해당 Section을 이해하기 위해서는 “Weisfeiler-Lehman Algorithm”이라고 생각할 수 있다. 해당 Section은 harryjo97 블로그에 매우 잘 정리되어있습니다. 해당 Section은 해당 블로그의 내용을 참고하여 작성하였습니다.

Graph Isomorphism
Graph Ismorphism이란 GCN에서 얘기한 Graph구조는 Location과 상관없이 Relationship을 고려해야 한다는 GCN과 같은 의미이다.

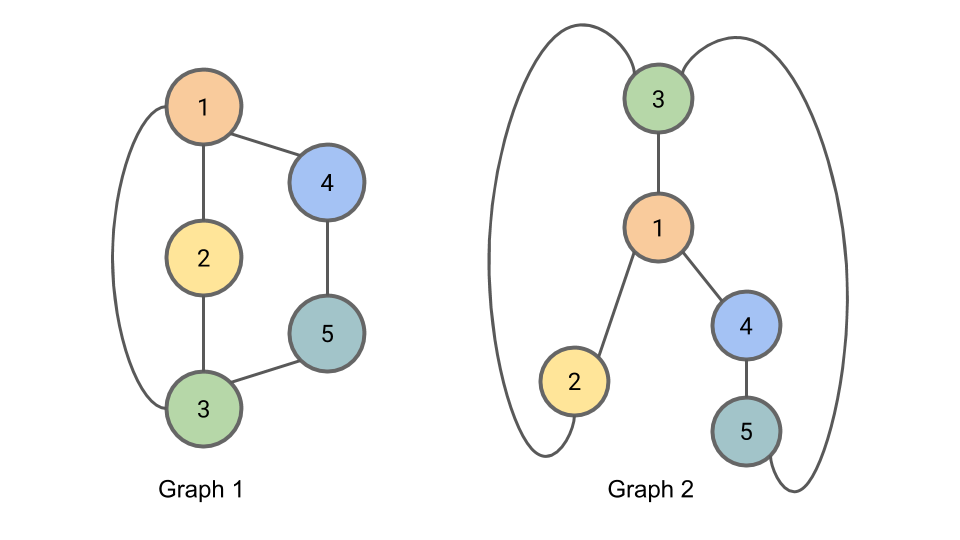
그림참조: harryjo97 블로그

위의 그림에서 Graph의 구조나 위치는 시각적으로 달라도 Relation은 같으므로 두 그래프는 isomorphic하다 라고 얘기한다.

Weisfeiler-Lehman Algorithm

그림참조: harryjo97 블로그

위의 Algorithm은 Weisfeiler-Lehman Algorithm에 관한 내용이다. 해당 Algorithm에 대한 내용은 아래에서 살펴보고, 해당 Algorithm에 대해 조심해야하는 점을 살펴보자.
Weisfeiler-Lehman Algorithm은 Graph isomorphic하다는 것을 완벽히 증명할 수는 없습니다. 하지만 아래와 같은 조건을 만족한다.

• \(\text{Graph isomorphic} \rightarrow \text{WL Algorithm}\)
• \(\text{WL Algorithm} \nrightarrow \text{Graph isomorphic}\)

즉, WL Algorithm을 만족한다고 Graph isomorphic하지 않지만, Graph isomorphic을 만족하기 위해서는 무조건 WL Algorithm을 만족하여야 한다. WL Algorithm의 자세한 내용은 아래와 같다.

먼저, 아래 그림과 같이 2개의 Graph가 있다고 가정하고, WL Algorithm을 적용해 보자.
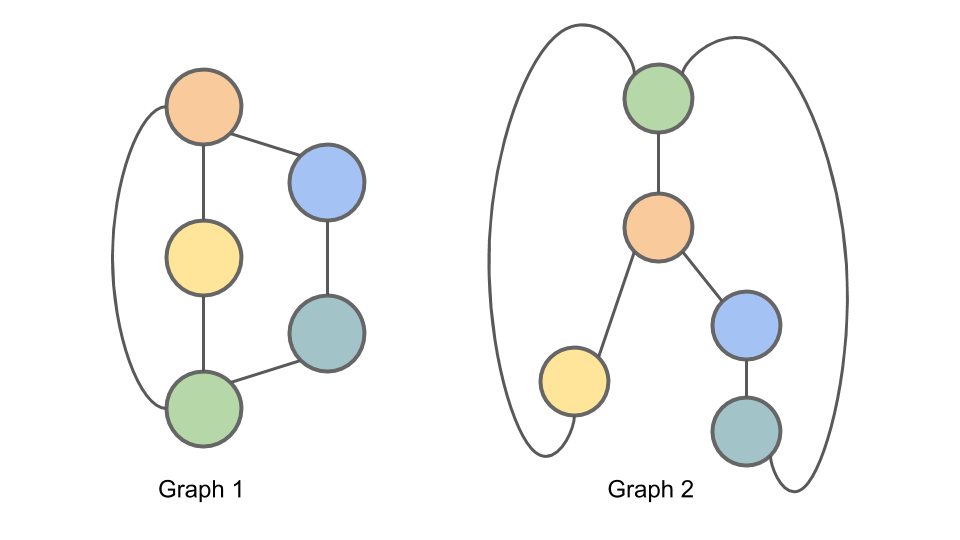
그림참조: harryjo97 블로그

다음으로, \(h_i^0=1\)로서 Initialization을 실시하자.
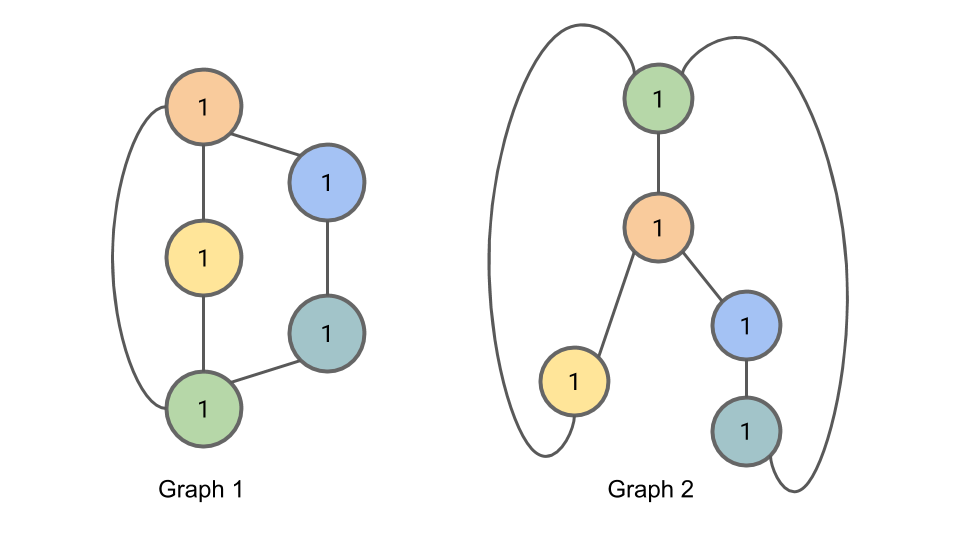
그림참조: harryjo97 블로그

이제 각 Node에 대하여 이웃된 Node의 값을 더해보자.
그림참조: harryjo97 블로그

해당 과정을 반복해서 확인하면서, 계속하여 일치하는지 확인하는 방법이 WL Algorithm이다.

WL Algorithm을 GraphSAGE embedding generation Algorithm에 대해 적용할 때, 아래와 같은 Setting으로 적용한다고 생각해보자.

• \(K = \| V \|\)
• \(W = \text{identity matrix}\)
• \(\text{aggregator without activation function} = \text{hash function}\)

위와 같이 생각하면 WL Algorithm과 동일하다는 것을 알 수 있다. 즉, GraphSAGE는 WL Algorithm의 hash function을 neural network aggregator로서 변형한 것을 알 수 있다.

그렇다면, 해당 논문의 저자는 해당 Section을 넣은 의도는 무엇일까? 개인적으로 생각할 때는 Sampling을 적용해야 하기 때문이라고 생각한다. 즉, \(\{ z_v, \forall v \in V\}\)로서 Sampling하였을 때, 5개의 sampling의 조합의 순서는 다를 수 있습니다. 즉, \(\{ h_u^{k-1}, u=\{1,2,3,4,5\} \}\)와 \(\{ h_u^{k-1}, u=\{5,4,3,1,2\} \}\)의 결과가 다르면 안된다는 것 이다.

결과적으로 Graph isomorphic를 유지할 수 있는 neural network aggregator를 선택하여야 한다는 것 이다.

Neighborhood definition

해당 논문의 저자들은 Sampling하여 선언하는 Neighborhood (\(N(v)\))에 대하여 Fixed and uniformly하게 Sampling하였다라고 적혀있습니다. 해당 저자들은 아래와 같은 Parameter로서 하였을 때, 성능이 가장 좋았다고 얘기하고 있습니다.

• \(K=2\): 최대 Hop=2로서 고정 하였다.
• \(S_1 \cdot S_2 <= 300\): Hop1과 Hop2의 Node개수를 곱하였을 때, 최대 500개 이하로서 Sampling하였다고 나와 있습니다.

Learning the parameters of GraphSAGE

$$J_{\mathbb{g}}(z_u) = -\log (\sigma (z_u^T z_v)) - Q \cdot \mathbb{E}_{v_n \sim P_n(v)} \log (\sigma(-z_{u}^T z_{v_n})) - (1)$$

• \(P_n\): negative sampling distribution
• \(Q\): number of negative samples

해당 수식의 의미는 특정 Node(\(z_u\))를 기준으로 이어져있는 Node (\(z_v\))와는 Representation이 비슷해지도록 학습하고, 이어져 있지 않은 Node(\(z_{v_n}\))과는 점점 멀어지도록 학습하는 방법이다.

원래 Binary Cross Entropy의 수식을 생각하면 아래와 같다.

$$BCE(x) = -\frac{1}{N}\sum_{i=1}^N y_i \log(h(x_i;\theta)) + (1-y_i) \log (1 - h(x_i;\theta))$$

BCE의 수식와 (1) 수식은 매우 유사하지만, Negative Sample인 경우에는 부등호가 반대인 것을 확인할 수 있다. 즉, 이어진 hidden representation과는 점점 비슷해지게, 이어져 있지 않는 것은 예측을 점점 못하게 학습한다는 것을 알 수 있다.

Aggregator Architecture

주변 Node들의 정보를 활용해서 특정 Node의 정보를 나타내기 Aggregate방법은 총 3개를 사용했다고 나와있다. 각각의 Aggregate 방법은 아래와 같다.

• Mean aggregator: \(h_v^k \leftarrow \sigma(W \cdot MEAN(\{h_v^{k-1}\} \cup \{h_u^{k-1}, \forall u \in N(v)\}) )\)
• LSTM aggregator
• Pooling aggregator: \(AGGREGATE_k^{pool} = max(\{ \sigma(W_{pool}h_{u_i}^k +b), \forall u_i \in N(v) \})\)

Mean aggregator
GCN에서도 사용한 방법이다. 자기 자신 뿐만 아니라 이어진 Node에 대하여 모두 평균을 취하여 Aggregator로서 사용하였다.

LSTM aggregator
해당 aggregator에 대해서는 수식으로서 적혀있지 않습니다. “저자들은 complex aggregator”를 사용하기 위하여 LSTM으로서 aggregator로서 사용하였다. 주요한 점은 LSTM Model은 Sequence Dataset에서 사용되는 Model로서 입력 순서가 주요한 Model이라는 것 이다. 이러한 문제점을 해결하기 위하여 해당 저자들은 node’s neighbors를 random permutation하여 입력으로 사용하였다고 한다.

Pooling aggregator
해당 Aggregator는 max 연산을 통하여 이웃 노드들의 feature중에서 최대값 (Elementwise max pooling)만 사용한다. 해당 저자들은 이러한 결과가 mean-pooling과 차이가 안난다고 이야기 하였다. (후에 실험은 max-pooling으로서 고정)

Appendix: Mean vs Max Pooling
해당 저자들의 실험결과에서 둘의 Aggregate 방법은 성능의 차이가 없다라고 밝히고 있다. 개인적인 생각으로는 이러한 실험결과를 얻기 위해서는 Embedding된 값 들의 feature가 Sparse한 상황이여야 한다고 생각합니다.

예를 들어, “User1”에 대한 정보는 “영화 선호도의 정보만 있고”, User 2에 대한 정보는 “영화관 재방문의 정보”만 있는 경우라고 생각한다. 이러한 Sparse한 상태이면, Mean과 Max pooling의 관계는 단순히 상수배인 관계로서 정의될 수 있다.

이러한 Dataset을 GNN으로서 학습하게 되면 특정 Node의 없는 정보를 Edge로서 이어진 Node에서 정보를 활용하여 예측할 수 있으며, Model의 Performance를 늘릴수 있다고 생각한다.

Experiment

해당 논문에서의 실험은 총 3개의 Dataset에서 실험을 진행하였으며, 기존의 SOTA모델들과 비교하였다.
주요한 것은 아래와 같이 Setting을 하고 GraphSAGE를 진행하였다는 것 이다.

• \(K=2\)
• \(S_1=25, S_2=10\)

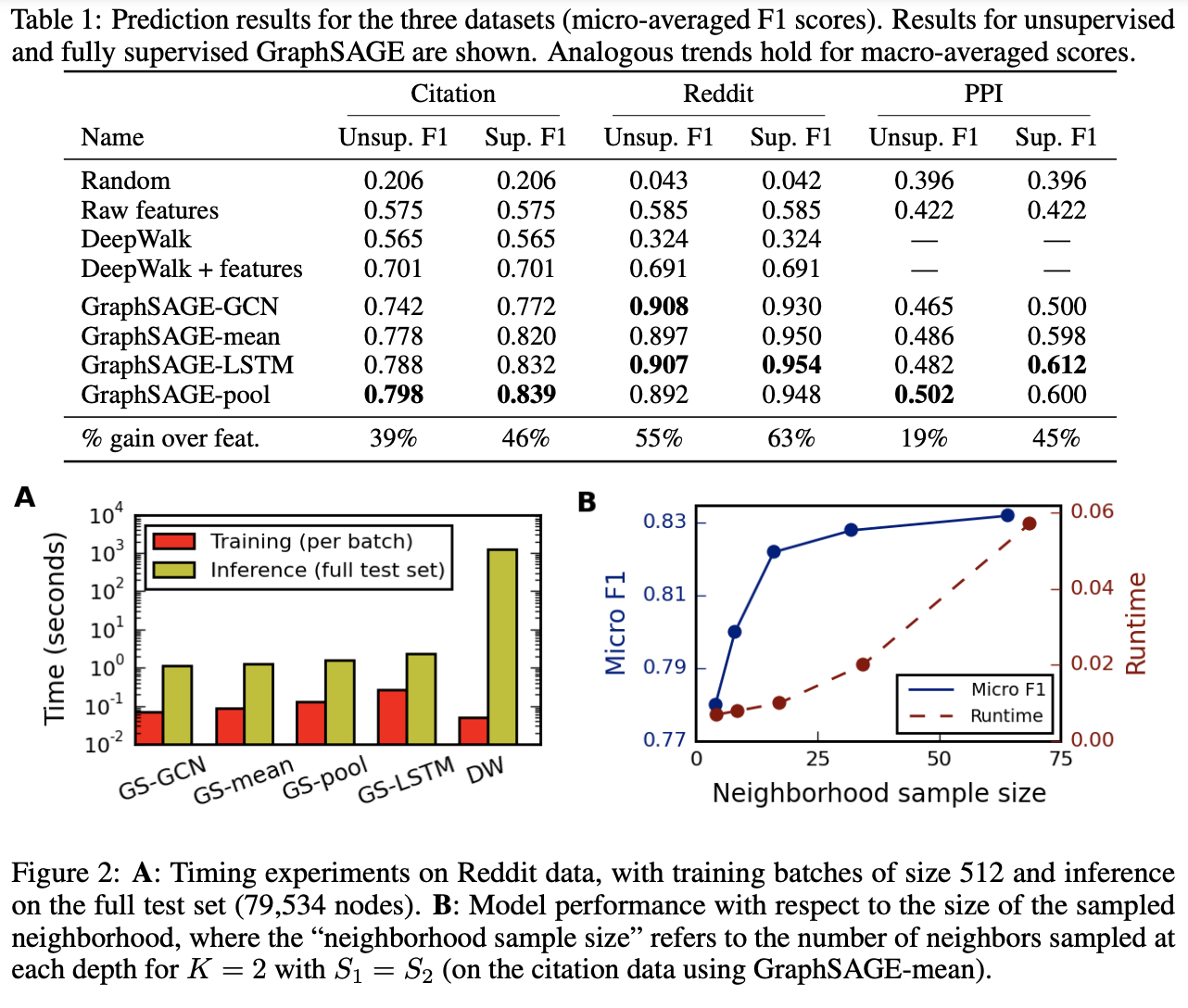
위의 실험에서 주요한 점은 4가지 이다.

• (1) 다른 Model들과 비교 하였을 때, 성능이 좋은 것을 알 수 있다.
• (2) 기존의 DeepWalk와 비교하였을 때, Training시간이 매우 단축되는 것을 알 수 있따.
• (3) \(AGGREGATE\) Function중에서 Pool이 대부분 성능이 좋았다.
• (4) Nieghborhood sample size가 증가할 수록 성능이 증가하지만, Runtime도 비하급수적으로 증가한다. 즉, 적절한 sample size를 정해야 합리적인 runtime을 얻을 수 있다.