Statistics(3)-Continuous probability distribution

이번 POST는 한양대학교 수리통계학 수업 내용을 정리한 것 입니다.
문제나 자세한 내용은 mykepzzang 블로그를 참조하였습니다.

5. 연속형 확률분포

(1) 일양분포(Uniform distribution)

연속형 확률변수 X의 밀도가 일정한 경우, 이러한 확률분포를 일양분포라 한다.
밀도함수 f(x)는 다음과 같다.

$$f(x) = \frac{1}{b-a}\text{ , } a< x < b$$

평균: \(E(x) = \frac{b+a}{2}\)

$$E(x) = \int_{-\infty}^{\infty}xf(x)\, dx = \int_{a}^{b} \frac{x}{b-a}\, dx$$

$$= [\frac{x^2}{2(b-a)}]^{b}_{a} = \frac{a+b}{2}$$

분산: \(V(x) = \frac{(b-a)^2}{12}\)

$$V(x) = E(X^2)-(E(x))^2 = \int_{a}^{b} \frac{x^2}{b-a}\, dx - \frac{(a+b)^2}{4}$$

$$= \frac{b^3-a^3}{3(b-a)} - \frac{(a+b)^2}{4} = \frac{(b-a)^2}{12}$$

문제) 어느 버스 정류장에 버스는 10분 간격으로 도착한다고 한다. 어떤 사람이 임의로 이 정류장에 와서 기다리는 시간이 균일분포를 따른다면, 이 사람이 5분 미만 기다릴 확률을 구하여라.

$$R_x = [0,10], f(x) = \frac{1}{10-0} = \frac{1}{10}$$

$$P(x<5) = \int_{0}^{5} \frac{1}{10}\, dx = \frac{1}{2}$$

(2) 정규분포(Normal distribution, Gaussian Distribution)

연속형 확률변수 X의 값이 중심값 근처에 대다수가 밀집되고 좌우 대칭의 종모양 분포를 가지는 경우, 이러한 확률분포를 정규분포라 하고, 기호로 \(X ~ N(\mu,\sigma^2)\)로 표현한다. 정규분포의 확률밀도함수 f(x)는 다음과 같다.

$$f(x) = \frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(x-\mu)^2}{2\sigma^2}}\text{ , 단, } -\infty \le X \le \infty\text{ , }e=2.71828...\text{ , }\pi=3.14\text{ 이다.}$$

평균: \(E(x) = \mu\)

$$E(x) = \int_{-\infty}^{\infty}xf(x)\, dx = \int_{-\infty}^{\infty}x\frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(x-\mu)^2}{2\sigma^2}}\, dx$$

$$= \frac{1}{\sqrt{2\pi}\sigma}(\int_{-\infty}^{\infty}(x-\mu)e^{-\frac{(x-\mu)^2}{2\sigma^2}}\, dx+\int_{-\infty}^{\infty}\mu e^{-\frac{(x-\mu)^2}{2\sigma^2}}\, dx)$$

위의 식에서 \(\int_{-\infty}^{\infty}(x-\mu)e^{-\frac{(x-\mu)^2}{2\sigma^2}}\, dx\)는 기함수로서 적분의 값이 0이나오게 된다.
따라서 최종적인 평균의 식은 다음과 같이 정리된다.

$$\therefore E(x) = \mu * \int_{-\infty}^{\infty}\frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(x-\mu)^2}{2\sigma^2}}\, dx\mu = \mu*\int_{-\infty}^{\infty}f(x;\mu,\sigma) \,dx = \mu$$

분산: \(V(x)^2 = \sigma\)

$$V(x) = E[(x-\mu^2)] = \int_{-\infty}^{\infty}(x-\mu^2)\,dx = \int_{-\infty}^{\infty} \frac{\sigma(x-\mu)^2}{\sqrt{2\pi}\sigma^2} e^{-\frac{(x-\mu)^2}{\sigma^2}} \,dx$$

위의 식에서 \(z = \frac{x-\mu}{\sigma}\)로 치환하게 되면 \(\frac{1}{\sigma}\frac{\partial x}{\partial z} = 1 \rightarrow dx=\sigma dz\)

$$\therefore \int_{-\infty}^{\infty} \frac{\sigma(x-\mu)^2}{\sqrt{2\pi}\sigma^2} e^{-\frac{(x-\mu^2)}{\sigma^2}} \,dx = \frac{\sigma^2}{\sqrt{2\pi}}\int_{-\infty}^{\infty} z^2 e^{-\frac{z^2}{2}} \,dz$$

위의 식에서 \(\int u(x)v^{'}(x) = u(x)v(x) - \int u^{'}(x)v(x)\)인 부분적분을 적용한다.
위의 부분적분 식에서 각각의 식에 다음과 같은 식으로서 대입한다.

$$u(x) = z \rightarrow u^{'}(x) = 1\text{ , } v^{'}(x) = ze^{-\frac{z^2}{2}} \rightarrow v(x) = -e^{-\frac{z^2}{2}}$$

$$\therefore \frac{\sigma^2}{\sqrt{2\pi}}\int_{-\infty}^{\infty} z^2 e^{-\frac{z^2}{2}} \,dz = \frac{\sigma^2}{\sqrt{2\pi}}([-ze^{-\frac{z^2}{2}}]_{-\infty}^{\infty} + \int_{-\infty}^{\infty} e^{-\frac{z^2}{2}}\,dz)$$

위의 식을 각각 나누어서 생각해보자.
식 \([-ze^{-\frac{z^2}{2}}]_{-\infty}^{\infty}\)에서 \(x=-z\)로서 치환하면 다음과 같은 식이 성립된다.

$$[-ze^{-\frac{z^2}{2}}]_{-\infty}^{\infty} = [xe^{-\frac{x^2}{2}}]_{\infty}^{-\infty} = 0 - 0 = 0$$

따라서 위의 식을 최종적으로 정리하면 다음과 같다.

$$V(x) = \frac{\sigma^2}{\sqrt{2\pi}} \int_{-\infty}^{\infty} e^{-\frac{z^2}{2}}\,dz = \sigma^2 \int_{-\infty}^{\infty} \frac{1}{\sqrt{2\pi}\sigma} e^{-\frac{(x-\mu^2)}{\sigma^2}} \,dx = \sigma^2 \int_{-\infty}^{\infty} N(\mu,\sigma^2) = \sigma^2$$

정규분포의 특징

1. 정규분포는 평균 \(\mu\)에 대하여 좌우 대칭이다.
2. 정규분포의 밀도함수는 평균 \(\mu\)와 표준편차 \(\sigma\)에 의해 변한다.
3. 정규분포 확률변수의 선형함수는 역시 정규분포를 따른다.(Z 변환 가능)

위의 2번을 시각적으로 표현하면 다음과 같다.
먼저 \(f(x;\mu,\sigma)\)의 그래프를 살펴보면 다음과 같다.

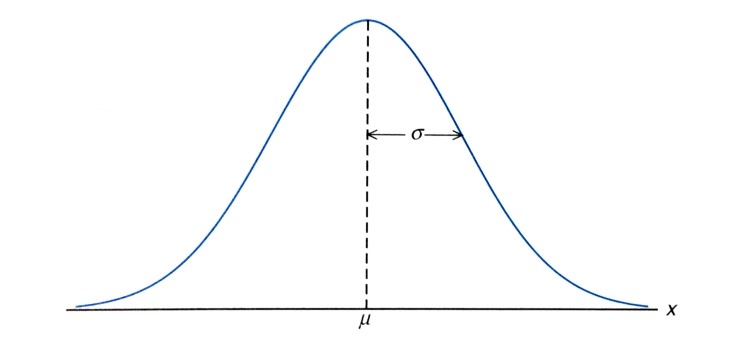
사진 출처: mykepzzang 블로그

위와 같이 기본적인 정규분포의 그래프를 바탕으로 각각의 상황에 대하여 알아보자.

1) 평균은 다르지만 표준편차는 같은 두 정규 곡선: \(\mu_1 < \mu_2, \sigma_1 = \sigma_2\)

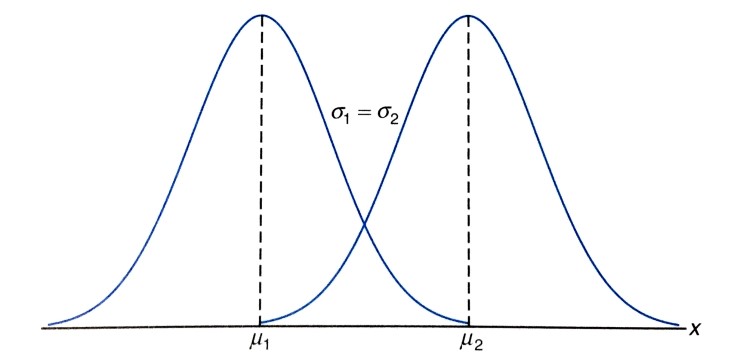
사진 출처: mykepzzang 블로그

2) 평균은 같고 표준편차는 다른 두 정규 곡선: \(\mu_1 = \mu_2, \sigma_1 < \sigma_2\)

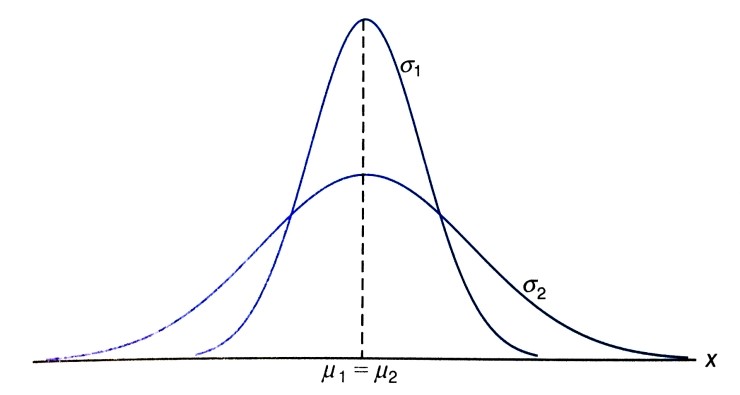
사진 출처: mykepzzang 블로그

3) 평균과 표준편차가 모두 다른 두 정규 곡선: \(\mu_1 < \mu_2, \sigma_1 < \sigma_2\)

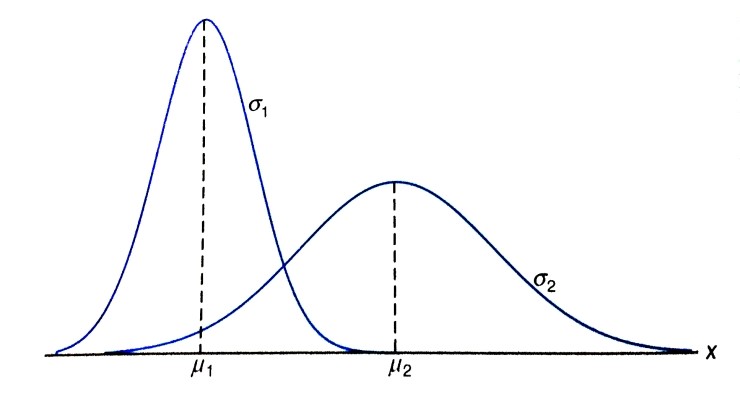
사진 출처: mykepzzang 블로그

정규분포의 구간확률: \(X \text{~} N(\mu,\sigma^2)\)
대부분의 정규분포의 확률은 아래와 같이 이미 정해져있는 정규분포표를 활용하여 구하게 된다.

1. \(P(\mu -1\sigma \le X \le \mu +1\sigma) = 0.6827\)
2. \(P(\mu -2\sigma \le X \le \mu +2\sigma) = 0.9545\)
3. \(P(\mu -3\sigma \le X \le \mu +3\sigma) = 0.9973\)

표준화
\(Z=\frac{x-\mu}{\sigma}\)는 평균이 0이고, 표준편차가 1인 특별한 정규분포를 따른다. 이때 Z는 표준정규분포를 따른다고 한다. 즉, \(Z \text{~} N(0,1)\)이다.
일반 정규분포 확률변수 X와 표준정규분포 확률변수 Z사이에는 1:1대응관계이므로, \(P(a<X<b) = P(\frac{a-\mu}{\sigma} < Z < \frac{b-\mu}{\sigma})\)
위의 표준화과정이 성립되는 이유를 살펴보면 다음과 같다.

$$E(Z) = E(\frac{X-\mu}{\sigma}) = \frac{1}{\sigma}E(X-\mu) = 0$$

$$V(Z) = V(\frac{X-\mu}{\sigma}) = \frac{1}{\sigma^2}V(X-\mu) = \frac{1}{\sigma^2}*\sigma^2 = 1$$

ex) 천명의 종원원을 고용하고 있는 회사가 있다. 이 회사의 종업원들의 근무연수는 평균 9년 , 표준편차 5년으로 정규분포를 이룬다고 한다. 종원원들 중에서 20년 이상 근무한 사람은 약 몇명인가?

$$P(X \ge 20) = P(Z \ge \frac{20-9}{5}) = 0.5 - P(Z \le 2.2) = 0.0139$$

(3) 감마분포(Gamma Distribution)

감마분포를 이해하기 위해서는 감마함수에 대해 먼저 이해해야 한다.
감마합수(Gamma function)
감마함수(Gamma function)은 계승(factorial)을 일반화한 형태(자연수 뿐만아니라 복소수까지 포함한 형태)의 함수로써, 다음과 같이 나타낸다.

$$\gamma(z) = \int_{0}^{\infty} x^{z-1} e^{-x}\, dx$$

$$\gamma(z) = \lim_{n \to \infty} \frac{1*2*3*...*n}{z(z+1)...(z+n)}n^z \text{ }(z \neq 0,-1,-2, ...)$$

Factorial을 일반화하였다는 것을 의미하기 위해서는 먼저 Gamma function의 특징 몇가지를 살펴보면 금새 이해할 수 있다.
1) \(\gamma(1) = 1\)

$$\gamma(1) = \int_{0}^{\infty}e^{-x}\, dx = [-e^{-x}]^{\infty}_{0} = 0 - (-1) = 1$$

2) \(\gamma(a+1) = a\gamma(a)\)

$$\gamma(a+1) = \int_{0}^{\infty} x^{a} e^{-x}\, dx = [-x^a e^{-x}]^{\infty}_{0} + \int_{0}^{\infty} ax^{a-1} e^{-x}\, dx$$

$$\because \text{부분 적분 사용}$$

$$=a\int_{0}^{\infty} ax^{a-1} e^{-x}\, dx = a\gamma(a)\text{ 단, }a>0$$

3) \(\gamma(n+1) = n!\)

$$\gamma(n+1) = n\gamma(n) = n(n-1)...(1)\gamma(1) = n!$$

위의 식을 살펴보면 복소수를 Factorial로서 일반화 할 수 있는 것을 알 수 있다.

감마분포(Gamma Distribution)은 감마함수로부터 감마분포의 확률밀도 함수를 유도한 것 이다.
감마분포(Gamma Distribution)의 의미는 \(\alpha\)번째 사건이 일어날떄까지 걸리는 시간에 대한 연속확률분포 이다.

감마함수의 식 \(\gamma(a) = \int_{0}^{\infty} x^{a-1} e^{-x}\, dx\)의 1이되면 확률로서 표현할 수 있다는 것을 알 수 있다.

$$1 = \int_{0}^{\infty} \frac{1}{\gamma(a)}x^{a-1} e^{-x}\, dx$$

$$\therefore f(x) = \frac{1}{\gamma(a)}x^{a-1} e^{-x}$$

위의 확률밀도 함수를 만족시키는 확률변수 X는 \(X \text{~} Gamma(a,1)\)을 따른다.

위의 식에서 좀 더 일반적인 감마분포의 확률밀도 함수를 구하면 다음과 같다.

$$ f(x;,\alpha,\beta)= \begin{cases} \frac{1}{\beta^{\alpha}\gamma(a)}x^{\alpha-1} e^{-\frac{x}{\beta}}, & \ x>0 \\ 0, & \mbox{elsewhere} \end{cases} $$

단, \(\alpha > 0, \beta > 0\)
위와 같은 감마분포의 확률밀도 함수에서 확률변수 X는 \(X \text{~} Gamma(\alpha,\beta)\)를 따르고 각각의 \(\alpha\)는 형태모수(shape parameter), \(\beta\)는 척도모수(scale parameter)이라고 한다.
각각의 모수에 따른 그래프는 다음과 같다.

Shape Scale 변화에 따른 감마분포 변화

그림 출처: support.minitab.com

평균: \(E(x) = \alpha\beta\)

$$E(x) = \int_{0}^{\infty} x f(x;\alpha,\beta)\, dx = \int_{0}^{\infty} \frac{1}{\beta^{\alpha}\gamma(a)}x^{\alpha} e^{-\frac{x}{\beta}}\, dx$$

$$= \int_{0}^{\infty} \frac{\alpha \beta}{\beta^{\alpha+1}\gamma(\alpha+1)}x^{\alpha} e^{-\frac{x}{\beta}}\, dx \text{ } \because(\gamma(\alpha + 1) = \alpha \gamma(\alpha))$$

$$=\alpha\beta\int_{0}^{\infty} \frac{1}{\beta^{\alpha+1}\gamma(\alpha+1)}x^{\alpha} e^{-\frac{x}{\beta}}\, dx = \alpha\beta\int_{0}^{\infty} f(x;\alpha+1,\beta)\, dx = \alpha\beta$$

분산: \(V(x) = \alpha\beta^2\)

$$V(x) = E(x^2) - (E(x))^2 = E(x^2) - (\alpha\beta)^2$$

$$E(x^2) = \int_{0}^{\infty} x^2 f(x;\alpha,\beta)\, dx = \int_{0}^{\infty} \frac{1}{\beta^{\alpha}\gamma(a)}x^{\alpha+1} e^{-\frac{x}{\beta}}\, dx$$

$$= \int_{0}^{\infty} \frac{\alpha(\alpha+1) \beta^2}{\beta^{\alpha+2}\gamma(\alpha+2)}x^{\alpha+1} e^{-\frac{x}{\beta}}\, dx$$

$$=\alpha(\alpha+1)\beta^2 \int_{0}^{\infty} \frac{1}{\beta^{\alpha+2}\gamma(\alpha+2)}x^{\alpha+1} e^{-\frac{x}{\beta}}\, dx = \alpha(\alpha+1)\beta^2\int_{0}^{\infty} f(x;\alpha+2,\beta)\, dx = \alpha(\alpha+1)\beta^2$$

$$\therefore V(x) = \alpha(\alpha+1)\beta^2 - (\alpha\beta)^2 = \alpha\beta^2$$

(4) 지수분포(Exponential Distribution)

지수분포는 감마분포의 특수한 경우이다. 특수한 경우라는 것은 감마분포의 \(\alpha=1\)인 경우 이다.
따라서 감마분포와 지수분포를 정의하면 다음과 같다.
감마분포

$$ f(x;,\alpha,\beta)= \begin{cases} \frac{1}{\beta^{\alpha}\gamma(a)}x^{\alpha-1} e^{-\frac{x}{\beta}}, & \ x>0 \\ 0, & \mbox{elsewhere} \end{cases} $$

지수분포

$$ f(x;,1,\beta)= \begin{cases} \frac{1}{\beta} e^{-\frac{x}{\beta}}, & \ x>0 \\ 0, & \mbox{elsewhere} \end{cases} $$

이러한 지수분포는 확률변수 X를 첫 고장이 발생할 때까지의 시간(lifetime)으로 정의하면 확률변수 X가 따르는 분포이다.

평균: \(E(x) = \beta\)

$$E(x) = \int_{0}^{\infty} xf(x)\,dx = \int_{0}^{\infty} \frac{x}{\beta} e^{-\frac{x}{\beta}}\,dx$$

위의 식에서 \(\frac{x}{\beta} = t\)로서 치환하면 식을 다음과 같이 나타낼 수 있다.

$$E(x) = \beta\int_{0}^{\infty} te^{-t}\,dt = \beta([-te^{-t}]_{0}^{\infty}+\int_{0}^{\infty} e^{-t}\,dt)$$

$$=\beta([-e^{-t}]_{0}^{\infty}) = \beta$$

분산: \(V(x) = \beta^2\)

$$E(x^2)-(E(x))^2 = E(x^2)-\beta^2$$

$$E(x^2)= \int_{0}^{\infty} \frac{x^2}{\beta} e^{-\frac{x}{\beta}}\,dx$$

$$=\beta^2 \int_{0}^{\infty} t^2e^{-t}\,dt$$

$$= \beta^2([-t^2 e^{-t}]_{0}^{\infty}+2 \int_{0}^{\infty} te^{-t}\,dt) = 2\beta^2$$

$$\therefore V(x) = 2\beta^2-\beta^2 = \beta^2$$

포아송분포와 지수분포의 관계
먼저 위에서 정의한 포아송분포의 정의부터 다시 살펴보면 다음과 같다.
확률변수 X를 시간 (0,t)에서 발생하는 사건의 수라 하면 확률함수 f(x)는 다음과 같다.

$$f(x) = \frac{e^{-\lambda t}(\lambda t)^x}{x!}$$

(단, \(\lambda\)= 단위 시간당 평균 발생 건수(모수), \(\lambda > 0, x=0,1,2,3,...\), e=2.71828… 이다.)

위의 포아송 분포에서 시간 t시간 에서 처음으로 사건이 발생하고 사건의 평균을 \(\lambda\)라하면 t전까지 확률변수는 0이되고 이것을 포아송분포의 확률함수로서 나타내면 다음과 같다.

$$f(0) = \frac{e^{-\lambda t}(\lambda t)^0}{0!} = e^{-\lambda t}$$

위의 식을 활용하여 사건이 처음 발생하기까지 걸린시간을 확률변수X라 하고, 이 확률변수 X가 시간 t를 초과하는 것은 아래와 같이 나타낼 수 있다.

$$P(X>t) = e^{-\lambda t}$$

여기서 확률변수 X에 대한 누적분포함수는 다음과 같다.

$$P(0 \le X \le t) = F(t) = 1-e^{-\lambda t}$$

누적분포함수를 미분하면 확률질량함수가 되므로 다음과 같은 식이 나오게 된다.

$$\frac{\partial F(t)}{\partial t} = \frac{\partial}{\partial t}(1-e^{-\lambda t})$$

$$\rightarrow f(t) = \lambda e^{-\lambda t}$$

즉 위의 식과 지수분포의 식을 비교하면 다음과 같다.

• 지수분포: \(\frac{1}{\beta} e^{-\frac{x}{\beta}}\)
• 포아송분포: \(\lambda e^{-\lambda t}\)

위의 식을 비교하게 되면 \(\frac{1}{\beta}=\lambda\)로서 표현 가능하다.
즉, 모수가 (\(\lambda t\))인 포아송 분포에서 연속적으로 발생하는 두 사건 사이의 경과시간을 확률시간 X로 했을 때(사건 발생 -> 초기화 -> 사건발생으로서 두 사건을 시간 0 ~ t까지의 처음 발생할때까지의 확률질량함수로서 표현하였다는 의미이다.), 이 확률변수 X는 지수분포를 따른다.

기하분포와 지수분포의 관계
먼저 기하분포(Geometric Distribution)의 정의를 살펴보게 되면 다음과 같다.
베르누이 시행에서 처음 성공까지 시도한 횟수 X의 분포, 지지집함은 {1,2,3,…}이다.

$$P(X=k) = (1-p)^{k-1}p$$

지수분포와 기하분포 둘 다 처음 실패 혹은 성공할때까지의 확률을 구하는 함수 이다.
이산형으로서 표현한 것이 기하분포, 연속형으로서 표현한 것이 지수분포 이다.
따라서 기하분포에서 \(n \rightarrow \infty\)로서 표현한 것이 지수분포인 것을 알 수 있다.

최종적인 관계를 생각해보면 다음 그림과 같이 나타낼 수 있다.

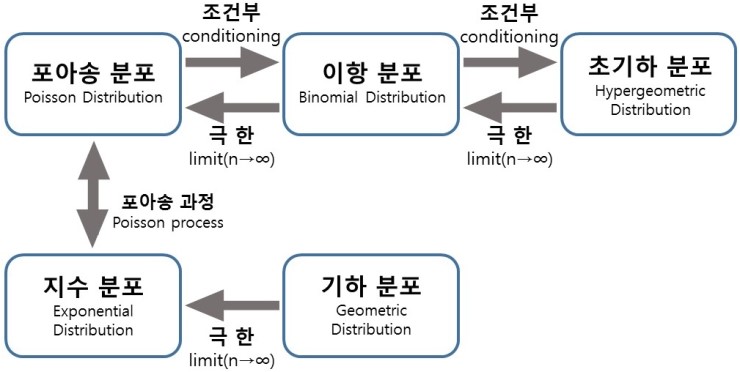
사진 출처: mykepzzang 블로그

ex) 고장횟수가 포아송 분포를 따르는 어떤 기계는 1개월에 평균 3번 고장을 일으킨다. 이 기계가 고장나서 고친 후 2개월 내에는 다시 고장나지 않을 확률을 구하여라.

확률밀도 함수: \(f(x) = \lambda e^{-\lambda x} = 3e^{-3x}\)
누적분포 함수: \(F(x) = 1 - e^{-\lambda x} = 1- e^{-3x}\)

$$P(X>2) - 1-P(0 \le X \le 2) = 1-F(2) = 1-e^{-6}$$

---

참조: 한양대학교 수리통계학 수업
참조: mykepzzang 블로그
코드에 문제가 있거나 궁금한 점이 있으면 wjddyd66@naver.com으로 Mail을 남겨주세요.