Statistics(6)-Central Limit Theorem

이번 POST는 한양대학교 수리통계학 수업 내용을 정리한 것 입니다.
문제나 자세한 내용은 mykepzzang 블로그를 참조하였습니다.

8. 중심극한정리(Central Limit Theorem)

중심극한 정리란 표본의 크기가 충분히 크면 표본평균의 분포를 정규분포로 근사시킬 수 있다.

중심극한정리를 위에서 정의한 적률함수의 특징으로서 나타낸다.
즉 정규분포의 적률함수(\(M_{x}(t)\)) = 정규분포의 적률분포 함수의 극한값(\(\lim_{n \to \infty}M_{\bar{x}}(t)\))가 같음을 보이는 것으로 증명한다.

(1)정규분포의 적률함수

$$f(x) = \frac{1}{\sqrt{2\pi}\sigma}e^{\frac{-(x-\mu)^2}{2\sigma^2}}$$

$$M_{x}(t) = \int_{-\infty}^{\infty}e^{xt}f(x)\,dx = \int_{-\infty}^{\infty}e^{xt}\frac{1}{\sqrt{2\pi}\sigma}e^{\frac{-(x-\mu)^2}{2\sigma^2}}\,dx$$

$$= \frac{1}{\sqrt{2\pi}\sigma} \int_{-\infty}^{\infty}e^{xt-\frac{(x-\mu)^2}{2\sigma^2}}\,dx$$

위의 식에서 e의 지수만을 생각해서 계산해보자.

$$xt-\frac{(x-\mu)^2}{2\sigma^2} = \frac{1}{2\sigma^2}(2\sigma^2 xt - (x-\mu)^2)$$

$$= \frac{1}{2\sigma^2}(2\sigma^2 xt - ((x-\mu)^2 -2(x-\mu)\sigma^2 t + (\sigma^2 t)^2 + 2(x-\mu)\sigma^2 t - (\sigma^2 t)^2))$$

$$= \frac{1}{2\sigma^2}(2\mu\sigma^2 t + \sigma^4 t^2 - (x-\mu-\sigma^2 t)^2)$$

$$\therefore M_{x}(t) = \int_{-\infty}^{\infty}e^{xt}f(x)\,dx = \int_{-\infty}^{\infty}e^{\frac{1}{2\sigma^2}(2\mu\sigma^2 t + \sigma^4 t^2 - (x-\mu-\sigma^2 t)^2)}\,dx$$

$$ = e^{\frac{1}{2}(2\mu t+\sigma^2 t^2)} \int_{-\infty}^{\infty}e^{-\frac{(x-\mu-\sigma^2 t)^2}{2\sigma^2}}\,dx$$

위의 식에서 \(\mu^{'} = \mu + \sigma^2 t\)라고 치환하면 식은 다음과 같이 정의된다.

$$= e^{\frac{1}{2}(2\mu t+\sigma^2 t^2)} \int_{-\infty}^{\infty}e^{-\frac{(x-\mu^{'})^2}{2\sigma^2}}\,dx$$

$$= e^{\frac{1}{2}(2\mu t+\sigma^2 t^2)}$$

따라서 최종적인 정규분포의 적률함수는 다음과 같이 나타낼 수 있다.

$$M_{x}(t) = e^{\frac{1}{2}(2\mu t+\sigma^2 t^2)}$$

(2)표본평균의 적률함수

표본평균의 적률함수는 다음과 같이 나타낼 수 있다.

$$N \text{~} (\mu,\sigma^2), \bar{X} \text{~} (\mu,\frac{\sigma^2}{n})$$

$$M_{\bar{x}}(t) = E(e^{\bar{x}t}) = E(e^{\frac{x_1+ x_2+ ... + x_n}{n}t}) = E(e^{\frac{x_1}{n}t}e^{\frac{x_2}{n}t}...e^{\frac{x_n}{n}t})$$

$$= E(e^{\frac{x_1}{n}t})E(e^{\frac{x_2}{n}t})...E(e^{\frac{x_n}{n}t}) = {E(e^{\frac{x}{n}t})}^n$$

위의 식에서 약간의 식 변형한다.

$$e^{\mu t}{E(e^{\frac{x-\mu}{n}t})}^n$$

위의 식에서 \(e^{\frac{x-\mu}{n}t}\)을 테일러 급수 전개를 하면 다음과 같다.

$$e^{\frac{x-\mu}{n}t} = 1+ \frac{(x-\mu)}{1!n}t+ \frac{(x-\mu)^2}{2!n^2}t^2+...$$

또한 위의 결과를 대입하기 전에 하나하나의 항의 기댓값을 구하면 다음과 같다.

$$E(\frac{(x-\mu)}{1!n}t) = \frac{t}{n}E(x-\mu) = 0$$

$$E(\frac{(x-\mu)^2}{2!n^2}t^2) = \frac{t}{n^2}E((x-\mu)^2) = \frac{t^2}{2!ㅜ^2}\sigma^2$$

또한 위의 표본평균의 분산을 활용하여 \($s^2 = \frac{\sigma^2}{n}\)$로서 나타내면 되종적인 식은 다음과 같다.

$$1+\frac{t^2}{2n}s^2+\frac{1}{n^2}(k)$$

위의 결과를 원래 구하고자 하였던, \(M_{\bar{x}}(t)\)에 대입하면 다음과 같다.

$$M_{\bar{x}}(t) = e^{\mu t}(1+\frac{t^2}{2n}s^2+\frac{1}{n^2}(k))$$

위의 식에서 n을 극한값을 주면 다음과 같다.

$$\lim_{n \to \infty} {M_{\bar{x}}(t)} = e^{\mu t + \frac{s^2 t^2}{2}}$$

따라서 최종적인 정규분포의 적률함수는 다음과 같이 나타낼 수 있다.

$$M_{\bar{x}}(t) = e^{\frac{1}{2}(2\mu t+s^2 t^2)}$$

최종적으로 구한 정규분포의 적률함수와 표본평균의 적률함수를 극값을 주었을 경우에 값이 같다는 것을 확인할 수 있다. 즉, 알 수 없는 모집단에서 표본이 충분히 크다면, 이 표본평균의 분포는 정규분포에 근사하다는 것 이다.

따라서 이전까지 배운 분포의 최종적인 관계를 표현하면 다음과 같이 표현할 수 있다.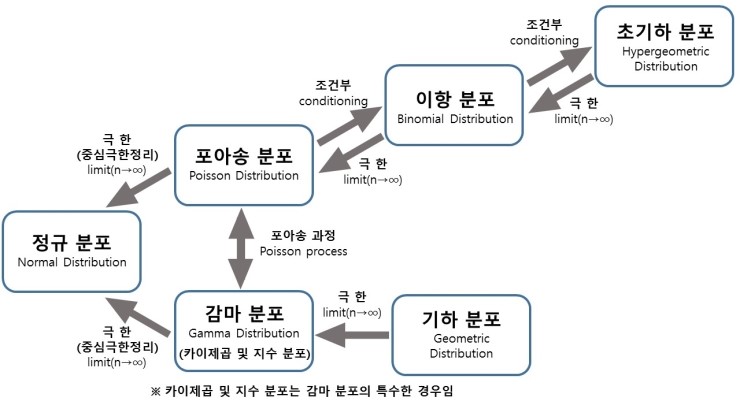
사진 출처: mykepzzang 블로그

---

참조: 한양대학교 수리통계학 수업
참조: mykepzzang 블로그
코드에 문제가 있거나 궁금한 점이 있으면 wjddyd66@naver.com으로 Mail을 남겨주세요.