DataAnalysis-양측검정,상관분석
양측검정
양측검정과 단측검정에 대해서 간단히 말하면
$$ 대립가설 \neq 이면 양측검정 $$
$$ 대립가설 > or < 이면 양측검정 $$
그렇다면 우리가 공부해왔던 카이제곱과 T검정은 양측검정인가?라는 의문이 든다.
이것에 대한 해답은 카이제곱과 T분포 그래프를 보면 이해하기 쉽다.
카이제곱 그래프
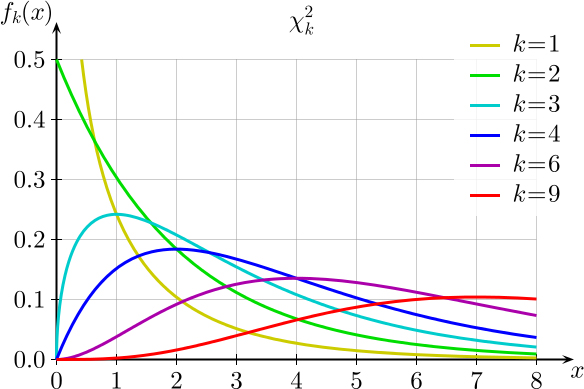
그림출처:존이 blog
T분포 그래프( 자유도가 10일 때, 확률이 0.05)

그림출처:godrag blog
위의 두 그래프를 살펴보게 되면 결국에는 그래프에서 단측만을 사용하므로 카이제곱과 T검정은 단측검정이라는 결론을 내릴수 있다.
아래는 양측검정의 예시이다.
| 귀무가설 | 임의 교육 수료 후, 80% 정도의 만족률을 보인다. |
| 대립가설 | 임의 교육 수료 후, 80% 정도의 만족률을 보이지 않는다. |
| 결과 | p-value(0.000673) < 0.05(95% 신뢰확률에서의 유의수준) => 대립가설 채택 |
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
#양측 검정 : 방향성이 없다. 80% 만족률 검증 실시
#귀무가설: 임의 교육 수료 후, 80% 정도의 만족률을 보인다.
#대립가설: 임의 교육 수료 후, 80% 정도의 만족률을 보이지 않는다.
print("---"*20)
print("양측 검정: 방향성이 없다. 80% 만족률 검증 실시")
data = pd.read_csv("https://raw.githubusercontent.com/wjddyd66/R/master/Data/one_sample.csv")
print("\ndata: ", data.head(3))
print("\ndata.describe(): ", data.describe())
ctab = pd.crosstab(index=data["survey"], columns="count")
ctab.index = ["불만족", "만족"]
print("\n ctab: ",ctab) # 불만족 14, 만족 136
result = stats.binom_test([136, 14], p=0.8, alternative="two-sided")
result2 = stats.binom_test([14, 136], p=0.2, alternative="two-sided")
# alternative -> 방향성 명시
# alternative= : {'two-sided','greater','less'} 선택 사항 :기본은 two-sided
print("\n result:",result) # p-value = 0.000673 < 0.05 (대립 채택)
print("result2:",result2)
# 기존 만족율 80% 라는 결과와는 차이가 있다.
# 검정 결과에서 '크다, 작다' 등의 방향성은 제시하지 않는다.
# 옵션을 반대로 입력해주어도 같은 결과를 보인다.
------------------------------------------------------------
양측 검정: 방향성이 없다. 80% 만족률 검증 실시
data: no gender survey time
0 1 2 1 5.1
1 2 2 0 5.2
2 3 2 1 4.7
data.describe(): no gender survey
count 150.000000 150.000000 150.000000
mean 75.500000 1.526667 0.906667
std 43.445368 0.500961 0.291874
min 1.000000 1.000000 0.000000
25% 38.250000 1.000000 1.000000
50% 75.500000 2.000000 1.000000
75% 112.750000 2.000000 1.000000
max 150.000000 2.000000 1.000000
ctab: col_0 count
불만족 14
만족 136
result: 0.0006734701362867019
result2: 0.000673470136286707
만족률이 더 클것이라고 가정한 경우
1
2
3
4
#만족률이 더 클것이라고 가정한 경우
result3 = stats.binom_test([136, 14], p=0.8, alternative="greater")
print("result3:",result3)
#p-value=0.000317 < 0.05 -> 대립 채택
result3: 0.0003179401921985477
만족률이 더 작을것이라고 가정한 경우
1
2
3
4
#만족률이 더 작을이라고 가정한 경우
result4 = stats.binom_test([14, 136], p=0.2, alternative="less")
print("result4:",result4)
#p-value=0.000317 < 0.05 -> 대립 채택
result4: 0.0003179401921985477
0을 기준으로서 대칭이르모 결과는 같다는 것을 살펴볼 수 있다.
상관 분석
상관 분석을 알기 위해서는 상관계수를 알아야 한다.
상관계수를 알기 위하여 공분산에 대하여 알아보자.
공분산(Covariance)란 각 확률변수 들이 어떻게 퍼져있는지를 나타내는 것이다.
아래 그림은 공분산에 대한 그림이다.

그림출처:destrudo blog
공분산은 아래와 같이 표시할 수 있다.
$$ Cov(X,Y) = E((X-u)(Y-v)) (u: X의 평균, v: Y의 평균)$$
공분산의 문제는 X와 Y의 단위의 크기에 영향을 받는다는 것이다.
즉 다시말해 100점만점인 두과목의 점수 공분산은 별로 상관성이 부족하지만 100점만점이기 때문에 큰 값이 나오고
10점짜리 두과목의 점수 공분산은 상관성이 아주 높을지만 10점만점이기 때문에 작은값이 나온다.
이를 보안하기 위해 상관계수(Correlation)이 나타난다.
상관계수는 크기에 영향을 받지 않도록 공분산을 단위화한 것이라고 생각할 수 있다.
상관계수는 아래와 같은 식으로서 나타낼 수 있다.
$$ p = \frac{Cov(X,Y)}{\sqrt{Var(X)Var(Y)}} (-1 \le p \le 1)$$
아래는 상관 분석을 알아본 것이다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
# 상관분석 : 두 변수 간에 어떤 선형적 관계가 있는지 분석. 밀도를 수치화
import pandas as pd
from pandas import Series
import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns
plt.rc('font', family='malgun gothic')
data = pd.read_csv("https://raw.githubusercontent.com/wjddyd66/R/master/Data/drinking_water.csv")
print(data.head(3))
print(data.describe())
print('\n공분산')
print(np.cov(data.친밀도, data.적절성))
print(np.cov(data.친밀도, data.만족도))
print()
print(data.cov())
print("\n상관계수")
print(np.corrcoef(data.친밀도, data.적절성))
print()
print(data.corr(method='pearson')) # 등간, 비율척도일때 주로 사용
# print(data.corr(method='spearman')) # 서열척도일때 주로 사용
# print(data.corr(method='kendall'))
# sns.heatmap(data.corr())
# plt.show()
# hitmap에 텍스트 표시 추가사항 적용해 보기
corr = data.corr()
# Generate a mask for the upper triangle
mask = np.zeros_like(corr, dtype=np.bool) # 상관계수값 표시
mask[np.triu_indices_from(mask)] = True
# Draw the heatmap with the mask and correct aspect ratio
vmax = np.abs(corr.values[~mask]).max()
fig, ax = plt.subplots() # Set up the matplotlib figure
sns.heatmap(corr, mask=mask, vmin=-vmax, vmax=vmax,
square=True, linecolor="lightgray", linewidths=1, ax=ax)
for i in range(len(corr)):
ax.text(i + 0.5, len(corr) - (i + 0.5), corr.columns[i],
ha="center", va="center", rotation=45)
for j in range(i + 1, len(corr)):
s = "{:.3f}".format(corr.values[i, j])
ax.text(j + 0.5, len(corr) - (i + 0.5), s, ha="center", va="center")
ax.axis("off")
plt.show()
친밀도 적절성 만족도
0 3 4 3
1 3 3 2
2 4 4 4
친밀도 적절성 만족도
count 264.000000 264.000000 264.000000
mean 2.928030 3.132576 3.094697
std 0.970345 0.859657 0.828744
min 1.000000 1.000000 1.000000
25% 2.000000 3.000000 3.000000
50% 3.000000 3.000000 3.000000
75% 4.000000 4.000000 4.000000
max 5.000000 5.000000 5.000000
0.9685051269352726
0.858027707764203
0.8271724742228972
공분산
[[0.94156873 0.41642182]
[0.41642182 0.73901083]]
[[0.94156873 0.37566252]
[0.37566252 0.68681588]]
친밀도 적절성 만족도
친밀도 0.941569 0.416422 0.375663
적절성 0.416422 0.739011 0.546333
만족도 0.375663 0.546333 0.686816
상관계수
[[1. 0.49920861]
[0.49920861 1. ]]
친밀도 적절성 만족도
친밀도 1.000000 0.499209 0.467145
적절성 0.499209 1.000000 0.766853
만족도 0.467145 0.766853 1.000000
상관관계 그래프로서 표현
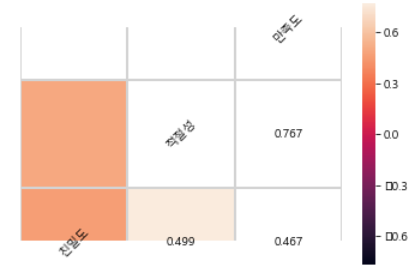
참조: 원본코드
코드에 문제가 있거나 궁금한 점이 있으면 wjddyd66@naver.com으로 Mail을 남겨주세요.

Leave a comment