DataAnalysis-Statistics
Statistics
통계에 대한 기초와 용어 정리는 아래 링크에 정리가 되어있습니다.
통계기초
이번 글에서는 Pandas를 활용하여 도수분포표 작성과 평균, 표준편차와 분산에 대해서 알아보자
도수분포표란 자료의 분표를 몇 개의 구간으로 나누고, 나누어진 각 구간에 속하는 자료가 몇 개인지 정리한 표이다.
구간으로 나누는 이유는 데이터의 기준을 정리하여서 Data를 읽고 활용하기 쉽게 가공하기 위해서 이다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
# 도수분포표
import pandas as pd
from pandas import DataFrame
url = "https://raw.githubusercontent.com/wjddyd66/R/master/Data/ex_studentlist.csv"
frame = pd.read_csv(url)
print(frame.head(3))
print(frame.shape)
print(frame.info())
print(frame.describe())
print("-")
# 혈액형 빈도수
data1 = frame.groupby(["bloodtype"])["bloodtype"].count()
print(data1)
data2 = pd.crosstab(index=frame["bloodtype"], columns=["count"])
print(data2)
print("-")
# 성별, 혈액형 빈도수 (2 way)
data3 = pd.crosstab(index=frame["bloodtype"],
columns=frame["sex"], margins=True)
# margins=True -> 소계 출력
data3.columns = ["남", "여", "행합"]
data3.index = ["A", "AB", "B", "O","열합"]
print(data3)
print("-")
print(data3 / data3.loc["열합", "행합"])
print("-")
# 행에 대한 열 비율
print(data3 / data3.loc["열합"])
print(data3.T / data3["행합"])
name sex age grade absence bloodtype height weight
0 김길동 남자 23 3 유 O 165.3 68.2
1 이미린 여자 22 2 무 AB 170.1 53.0
2 홍길동 남자 24 4 무 B 175.0 80.1
(15, 8)
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 15 entries, 0 to 14
Data columns (total 8 columns):
name 15 non-null object
sex 15 non-null object
age 15 non-null int64
grade 15 non-null int64
absence 15 non-null object
bloodtype 15 non-null object
height 15 non-null float64
weight 15 non-null float64
dtypes: float64(2), int64(2), object(4)
memory usage: 1.1+ KB
None
age grade height weight
count 15.000000 15.000000 15.000000 15.000000
mean 22.333333 2.266667 170.186667 60.380000
std 1.112697 1.032796 8.378533 12.408591
min 20.000000 1.000000 155.200000 45.200000
25% 22.000000 1.500000 163.750000 52.500000
50% 22.000000 2.000000 170.100000 55.300000
75% 23.000000 3.000000 176.500000 66.200000
max 24.000000 4.000000 182.100000 85.700000
-
bloodtype
A 3
AB 3
B 4
O 5
Name: bloodtype, dtype: int64
col_0 count
bloodtype
A 3
AB 3
B 4
O 5
-
남 여 행합
A 1 2 3
AB 2 1 3
B 3 1 4
O 2 3 5
열합 8 7 15
-
남 여 행합
A 0.066667 0.133333 0.200000
AB 0.133333 0.066667 0.200000
B 0.200000 0.066667 0.266667
O 0.133333 0.200000 0.333333
열합 0.533333 0.466667 1.000000
-
남 여 행합
A 0.125 0.285714 0.200000
AB 0.250 0.142857 0.200000
B 0.375 0.142857 0.266667
O 0.250 0.428571 0.333333
열합 1.000 1.000000 1.000000
A AB B O 열합
남 0.333333 0.666667 0.75 0.4 0.533333
여 0.666667 0.333333 0.25 0.6 0.466667
행합 1.000000 1.000000 1.00 1.0 1.000000
평균, 표준편차, 분산
평균은 모든 데이터의 값을 더하고, 데이터의 개수로 나눈 값이다. 중심성향에 대한 추정량을 계산할 때 사용한다.
이러한 평균은 아래의 식으로서 나타낼 수 있다.
$$ mean(x) = \frac{1}{n} \sum_{i=1}^{n}x_i $$
표준 편차에 대해서 알기전에 편차에 대해서 알아야 한다.
편차란 하나의 데이터 값이 평균에서 얼마나 떨어져있는지에 대한 값이다.
이러한 편차들은 양수와 음수의 값을 가지고 있기 때문에 평균값에서 실제값이 얼마나 오류가 있는지 판단할 수 없다.
이러한 편차들의 합을 양수화 하기 위해 제곱을 사용한다.
분산은 이러한 편차들의 제곱의 합을 계산한 것이다.
이러한 분산은 아래의 식으로서 나타낼 수 있다.
$$ var(x) = \frac{1}{n}\sum_{i=1}^{n}(x_i-mean(x))^2 $$
분산은 편차들의 제곱의 합이므로 실제 값에서 너무 떨어지게 된다. 따라서 이러한 오차의 값을 구하기 위해서 제곱근에 루트를 씌워준 값이 표준편차가 된다.
즉, 표준편차는 평균으로부터 원래 데이터에 대한 오차범위의 근사값 = 흩어진 정도에 대한 척도가 된다.
이러한 표준편차는 아래의 식으로서 나타낼 수 있다.
$$ std(x) = var(x)^{\frac{1}{2}} $$
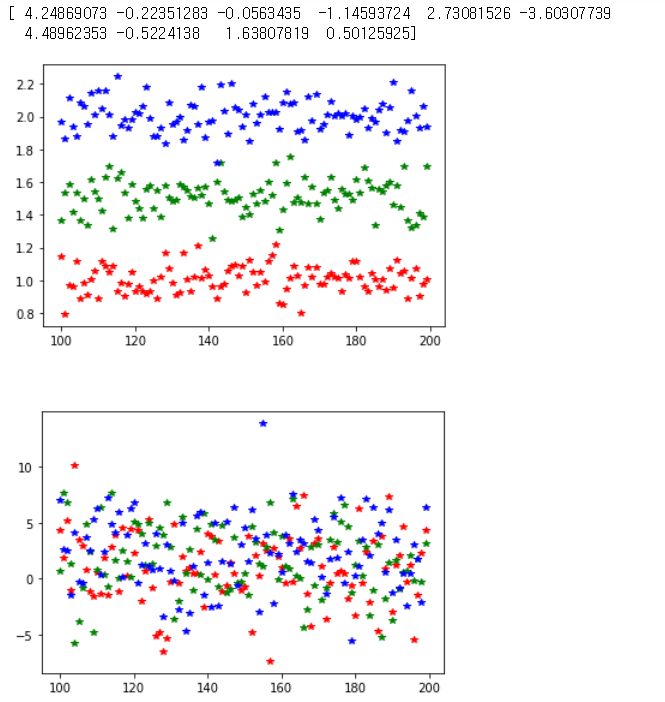
아래 예시는 실제 표준편차에 따라서 Data의 분포를 알아보는 예시이다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
# 분산의 중요성
import scipy.stats as stats
import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
np.random.seed(1)
print(stats.norm(loc=1, scale=2).rvs(10))
center = [1, 1.5, 2]
col = "rgb"
std = 0.1 #표준편차
data_1 = []
for i in range(3):
data_1.append(stats.norm(center[i], std).rvs(100))
plt.plot(np.arange(len(data_1[i])) + len(data_1[0] * i),
data_1[i], "*", color = col[i])
plt.show()
print()
std = 3 #표준편차
data_2 = []
for i in range(3):
data_2.append(stats.norm(center[i], std).rvs(100))
plt.plot(np.arange(len(data_2[i])) + len(data_2[0] * i),
data_2[i], "*", color = col[i])
plt.show()
참조: 원본코드
참초:ocurcstory 블로그
코드에 문제가 있거나 궁금한 점이 있으면 wjddyd66@naver.com으로 Mail을 남겨주세요.

Leave a comment