NeuralNetwork (3) Optimazation2
Optimazation 고려사항
Optimazation을 하기 위한 고려사항은 크게 3가지가 있다.
- Local Minima
- Plateau
- Zigzag
Local Minima
Local minima 문제는 에러를 최소화시키는 최적의 파라미터를 찾는 문제에 있어서 아래 그림처럼 파라미터 공간에 수많은 지역적인 홀(hole)들이 존재하여 이러한 local minima에 빠질 경우 전역적인 해(global minimum)를 찾기 힘들게 되는 문제를 일컫는다.

그림출처:nittaku 블로그
실제 딥러닝 모델에서는 Weight가 수도없이 많으며, 그 수많은 Weight가 모두 Local minima에 빠져야 Weight Update가 정지되기 때문에 불가능하다. Local Minima을 해결하기 위하여 Optimization을 할 이유는 없다.
Plateau
Gradient Descent를 타고 Global Optima를 향해서 나아가는데, 평지(Plateau)가 생겨 loss가 업데이트 되지 않는 현상이 발생한다. 이러한 것을 Plateau현상 이라고 한다. 또한 Local Minima에 비해 일어날 확률이 매우 높다.

그림출처:nittaku 블로그
ZigZag현상
Weight를 Update 시키기 위한 BackPropagation을 Chain Rule에 적용시킨 결론은 아래와 같았다.
$$\delta (n-1) = \delta ng\prime(x) W$$
BackPropagation 자세한 내용
Active Function을 Sigmoid나 Relu를 사용하게 되면, \(\delta n\)(output: 0~1) 및 \(g\prime(x)\)(Sigmoid의 편미분)이 모두 양수이므로 Weight업데이트량은 언제나 + or -가 나오며, 업데이트 방향을 잡을 때, 비효율적으로 ZigZag현상이 발생하여, 업데이트 현상이 느려진다.
우리가 지금까지 사용해온Gradient Descent 로서는
- Local Minima
- Plateau
- ZigZag현상
위의 3개를 해결할 수 없다.
Optimazation 방법
Gradient Descent
Gradient Descent 방법은 아래와 같이 구현될 수 있다.
1
2
3
4
5
6
7
8
9
10
class SGD:
"""확률적 경사 하강법(Stochastic Gradient Descent)"""
def __init__(self, lr=0.01):
self.lr = lr
def update(self, params, grads):
for key in params.keys():
params[key] -= self.lr * grads[key]
이러한 방법은 위의 3가지 문제를 해결 할 수 없으므로 다른 방법에 대해 알아보자.
Momentum
Local Minima에 덜 빠지기 위해 Learning Rate에게 일종의 관성이라 할 수 있는 Momentum을 둔다. 직전에 나온 방향성 즉, 직전에 계산된 기울기를 고려하여 새로 계산된 기울기와 일정한 비율로 계산을 하는 것이다. 이렇게 하면 기울기가 갑자기 양수에서 음수로, 음수에서 양수로 바뀌는 경우가 줄어 들게 되고, 완만한 경사를 더 쉽게 타고 넘을 수 있게 된다.
하지만 ZigZag 현상을 완벽히 해결하지는 못한다.

그림출처:nittaku 블로그
위의 그림은 아래 수식으로서 간단히 표현할 수 있다.
$$ v \leftarrow \alpha v - \beta \frac{\partial L}{\partial \theta} $$
$$ \theta \leftarrow \theta + v $$
새로운 하이퍼 파라미터인 \(\alpha , v\)가 새롭게 추가되 미분값이 계속하여 v에 더해져서 더욱 큰 값을 갖게되어 Plateau나 뭉뚱한 부분에서느림, Local Minima의 3가지를 해결할 수 있다.
Momentum 방법은 아래와 같이 구현될 수 있다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Momentum:
"""모멘텀 SGD"""
def __init__(self, lr=0.01, momentum=0.9):
self.lr = lr
self.momentum = momentum
self.v = None
def update(self, params, grads):
if self.v is None:
self.v = {}
for key, val in params.items():
self.v[key] = np.zeros_like(val)
for key in params.keys():
self.v[key] = self.momentum*self.v[key] - self.lr*grads[key]
params[key] += self.v[key]
AdaGrad
Adagrad(Adaptive Gradinet)는 변수들을 update할 때 각각의 변수마다 step size를 다르게 설정해서 이동하는 방식이다.
‘지금까지 많이 변화하지 않은 변수들은’ step size를 크게 하고,
‘지금까지 많이 변화한 변수들은’ step size를 작게 하자’는 것 이다.
즉, 자주 등장하거나 변화를 많이한 변수들의 경우 optimum에 가까이 있을 확률이 높기 때문에 작은 크기로 이동하면서 세밀한 값을 조정하고, 적게 변화한 변수들은 optimum값에 도달하기 위해서는 많이 이동해야 하므로 빠르게 loss값을 줄이는 방향으로 이동하는 방식이다.

그림출처:nittaku 블로그
위의 그림은 아래 수식으로서 간단히 표현할 수 있다.
$$G_t = G_{t-1} + (\nabla_{\theta}J(\theta_t))^{2}$$
$$\theta_{t+1} =\theta_{t} - \frac{\alpha}{\sqrt{G_t + \beta}} \bullet \nabla_{\theta}J(\theta_t)$$
\(G_t\)는 time step t까지 각 변수가 이동한 gradinet의 sum of squeares를 저장한다.
계속해서 값을 누적하는 형태이므로 나누어주는 수(\(G_t\))가 결국에는 커져 w업데이트가 너무 느려진다.
\(\alpha\) 는 \(G_t\)루트값에 반비례한 크기로 이동을 진행하여, 지금까지 많이 변화한 변수일 수록 적게 이동, 지금까지 많이 이동한 변수일수록 적게 이동을 하게 곱해주게 된다.
즉, 모든 Weight들은 업데이트량이 비슷해지는 효과가 발생하게 된다.
\(\beta\) 는 \(10^{-4} ~ 10^{-8}\)정도의 작은 값으로서 0으로 나누는 것을 방지하기 위한 작은 값이다.
AdaGrad 방법은 아래와 같이 구현될 수 있다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class AdaGrad:
"""AdaGrad"""
def __init__(self, lr=0.01):
self.lr = lr
self.h = None
def update(self, params, grads):
if self.h is None:
self.h = {}
for key, val in params.items():
self.h[key] = np.zeros_like(val)
for key in params.keys():
self.h[key] += grads[key] * grads[key]
params[key] -= self.lr * grads[key] / (np.sqrt(self.h[key]) + 1e-7)
RMS Prop
Adagrad의 단점을 해결하기 위한 방법이다.
\(G_t\)부분을 합이 아니라 지수평균으로 바꾸어서 대처한 방법이다.
이렇게 대체를 할 경우 Adagrad처럼 \(G_t\)가 무한정 커지지는 않으면서 최근 변화량의 변수간 상대적인 크기 차이는 유지할 수 있다.

그림출처:nittaku 블로그
위의 그림은 아래 수식으로서 간단히 표현할 수 있다.
$$G = \alpha G + (1 - \alpha)(\nabla_{\theta}J(\theta_t))^{2}$$
$$\theta =\theta - \frac{\alpha}{\sqrt{G + \beta}} \bullet \nabla_{\theta}J(\theta_t)$$
RMS Prop 방법은 아래와 같이 구현될 수 있다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class RMSprop:
"""RMSprop"""
def __init__(self, lr=0.01, decay_rate = 0.99):
self.lr = lr
self.decay_rate = decay_rate
self.h = None
def update(self, params, grads):
if self.h is None:
self.h = {}
for key, val in params.items():
self.h[key] = np.zeros_like(val)
for key in params.keys():
self.h[key] *= self.decay_rate
self.h[key] += (1 - self.decay_rate) * grads[key] * grads[key]
params[key] -= self.lr * grads[key] / (np.sqrt(self.h[key]) + 1e-7)
Adam
Adam (Adaptive Moment Estimation)은 RMSProp과 Momentum 방식을 합친 것 같은 알고리즘이다. 이 방식에서는 Momentum 방식과 유사하게 지금까지 계산해온 기울기의 지수평균을 저장하며, RMSProp과 유사하게 기울기의 제곱값의 지수평균을 저장한다.

그림출처:nittaku 블로그
위의 그림은 아래 수식으로서 간단히 표현할 수 있다.
$$m_t = \beta_1 m_{t-1} + (1 - \beta_1)\nabla_{\theta}J(\theta)$$
$$v_t = \beta_2 v_{t-1} + (1 - \beta_2)(\nabla_{\theta}J(\theta))^{2}$$
다만 m과 v가 처음에 0으로 초기화되어있기 때문에 초기 w업데이트 속도가 느리다는 단점이 생기게 된다. Adam 방법은 아래와 같이 구현될 수 있다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
class Adam:
"""Adam (http://arxiv.org/abs/1412.6980v8)"""
def __init__(self, lr=0.001, beta1=0.9, beta2=0.999):
self.lr = lr
self.beta1 = beta1
self.beta2 = beta2
self.iter = 0
self.m = None
self.v = None
def update(self, params, grads):
if self.m is None:
self.m, self.v = {}, {}
for key, val in params.items():
self.m[key] = np.zeros_like(val)
self.v[key] = np.zeros_like(val)
self.iter += 1
lr_t = self.lr * np.sqrt(1.0 - self.beta2**self.iter) / (1.0 - self.beta1**self.iter)
for key in params.keys():
#self.m[key] = self.beta1*self.m[key] + (1-self.beta1)*grads[key]
#self.v[key] = self.beta2*self.v[key] + (1-self.beta2)*(grads[key]**2)
self.m[key] += (1 - self.beta1) * (grads[key] - self.m[key])
self.v[key] += (1 - self.beta2) * (grads[key]**2 - self.v[key])
params[key] -= lr_t * self.m[key] / (np.sqrt(self.v[key]) + 1e-7)
#unbias_m += (1 - self.beta1) * (grads[key] - self.m[key]) # correct bias
#unbisa_b += (1 - self.beta2) * (grads[key]*grads[key] - self.v[key]) # correct bias
#params[key] += self.lr * unbias_m / (np.sqrt(unbisa_b) + 1e-7)
Optimazation 비교
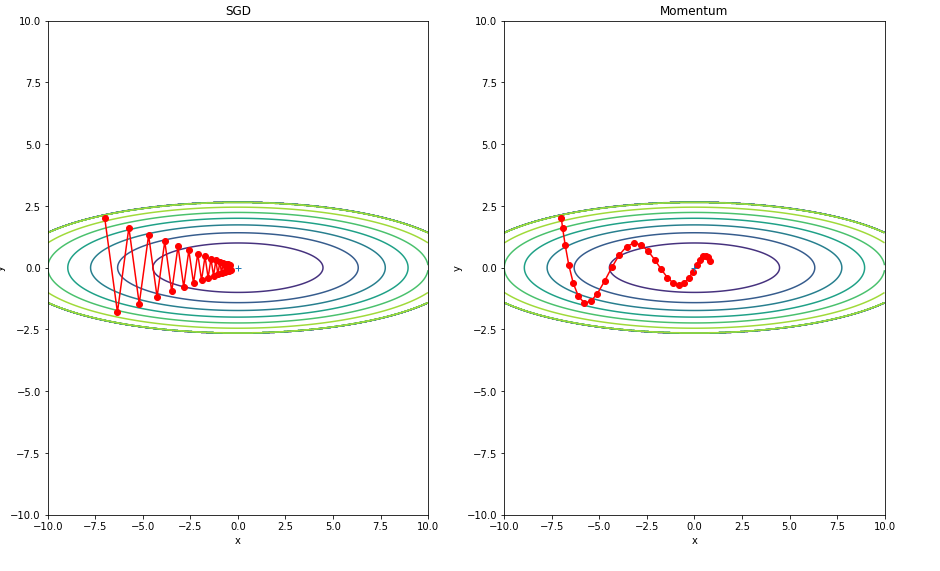
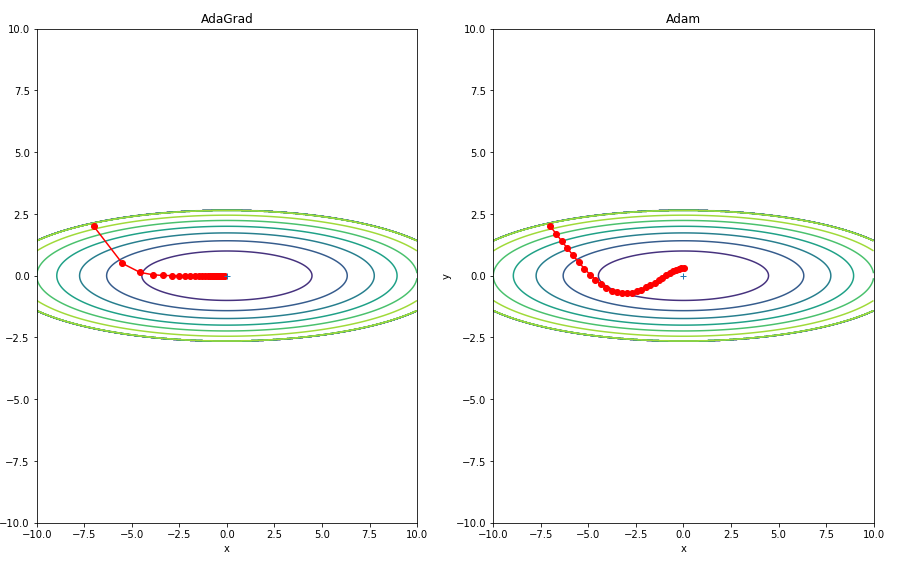
위에서 구현하였던 Optimazation의 학습 방법을 비교하기 위하여 그래프로서 학습 패턴을 비교한다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
#학습 패턴 비교
def f(x, y):
return x**2 / 20.0 + y**2
def df(x, y):
return x / 10.0, 2.0*y
init_pos = (-7.0, 2.0)
params = {}
params['x'], params['y'] = init_pos[0], init_pos[1]
grads = {}
grads['x'], grads['y'] = 0, 0
optimizers = OrderedDict()
optimizers["SGD"] = SGD(lr=0.95)
optimizers["Momentum"] = Momentum(lr=0.1)
optimizers["AdaGrad"] = AdaGrad(lr=1.5)
optimizers["Adam"] = Adam(lr=0.3)
idx = 1
for key in optimizers:
optimizer = optimizers[key]
x_history = []
y_history = []
params['x'], params['y'] = init_pos[0], init_pos[1]
for i in range(30):
x_history.append(params['x'])
y_history.append(params['y'])
grads['x'], grads['y'] = df(params['x'], params['y'])
optimizer.update(params, grads)
x = np.arange(-10, 10, 0.01)
y = np.arange(-5, 5, 0.01)
X, Y = np.meshgrid(x, y)
Z = f(X, Y)
# 외곽선 단순화
mask = Z > 7
Z[mask] = 0
# 그래프 그리기
plt.rcParams["figure.figsize"] = (15,20)
plt.subplot(2, 2, idx)
idx += 1
plt.plot(x_history, y_history, 'o-', color="red")
plt.contour(X, Y, Z)
plt.ylim(-10, 10)
plt.xlim(-10, 10)
plt.plot(0, 0, '+')
#colorbar()
#spring()
plt.title(key)
plt.xlabel("x")
plt.ylabel("y")
plt.show()
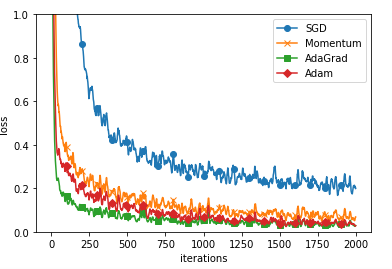
위에서 구현하였던 Optimazation의 학습 방법을 비교하기 위하여 그래프로서 학습 속도을 비교한다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
from dataset.mnist import load_mnist
from common.util import smooth_curve
from common.multi_layer_net import MultiLayerNet
from common.optimizer import *
# 0. MNIST 데이터 읽기==========
(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True)
train_size = x_train.shape[0]
batch_size = 128
max_iterations = 2000
# 1. 실험용 설정==========
optimizers = {}
optimizers['SGD'] = SGD()
optimizers['Momentum'] = Momentum()
optimizers['AdaGrad'] = AdaGrad()
optimizers['Adam'] = Adam()
#optimizers['RMSprop'] = RMSprop()
networks = {}
train_loss = {}
for key in optimizers.keys():
networks[key] = MultiLayerNet(
input_size=784, hidden_size_list=[100, 100, 100, 100],
output_size=10)
train_loss[key] = []
# 2. 훈련 시작==========
for i in range(max_iterations):
batch_mask = np.random.choice(train_size, batch_size)
x_batch = x_train[batch_mask]
t_batch = t_train[batch_mask]
for key in optimizers.keys():
grads = networks[key].gradient(x_batch, t_batch)
optimizers[key].update(networks[key].params, grads)
loss = networks[key].loss(x_batch, t_batch)
train_loss[key].append(loss)
if i % 100 == 0:
print( "===========" + "iteration:" + str(i) + "===========")
for key in optimizers.keys():
loss = networks[key].loss(x_batch, t_batch)
print(key + ":" + str(loss))
# 3. 그래프 그리기==========
markers = {"SGD": "o", "Momentum": "x", "AdaGrad": "s", "Adam": "D"}
x = np.arange(max_iterations)
for key in optimizers.keys():
plt.plot(x, smooth_curve(train_loss[key]), marker=markers[key], markevery=100, label=key)
plt.xlabel("iterations")
plt.ylabel("loss")
plt.ylim(0, 1)
plt.legend()
plt.show()
===========iteration:0===========
SGD:2.358243771682116
Momentum:2.507310950791858
AdaGrad:2.251947694538095
Adam:2.2173404849659124
===========iteration:100===========
SGD:1.7731225587273771
Momentum:0.514392494820839
AdaGrad:0.23176758910418443
Adam:0.3760409017865781
...
===========iteration:1800===========
SGD:0.17170440649380625
Momentum:0.05949062388159548
AdaGrad:0.02814846322935028
Adam:0.028274543618555692
===========iteration:1900===========
SGD:0.2500616367457645
Momentum:0.10463024189850922
AdaGrad:0.029562518793861896
Adam:0.026213455567180126
참조: 원본코드
참조: Chanwoo Timothy Lee Youtube
참조: 나무위키
참조: 밑바닥부터 시작하는 딥러닝
문제가 있거나 궁금한 점이 있으면 wjddyd66@naver.com으로 Mail을 남겨주세요.

Leave a comment