NeuralNetwork (4) Backpropagation1

Chain Rule

Backpropagation을 알기전에 Chain Rule이라는 것을 먼저 알아야 한다.
Chain Rule은 합성함수의 미분법이다.
n변수 함수 \(f(x_1,x_2,x_3,...,x_n)\)에 대해
\(x_k = g_k(t_1,t_2,t_3,...,t_m) (k=1,2,3,...,n)\)이면
\(\frac{\partial f}{\partial t_i}=\frac{\partial f}{\partial x_1}\frac{\partial x_1}{\partial t_i}+\frac{\partial f}{\partial x_2}\frac{\partial x_2}{\partial t_i}+...+\frac{\partial f}{\partial x_n}\frac{\partial x_n}{\partial t_i} (i=1,2,3,...,m)\)이다.
Chain Rule에대한 자세한 내용:Nenyaffle 블로그

계산 그래프(computational graph)는 계산과정을 그래프로 나타낸 것이다.
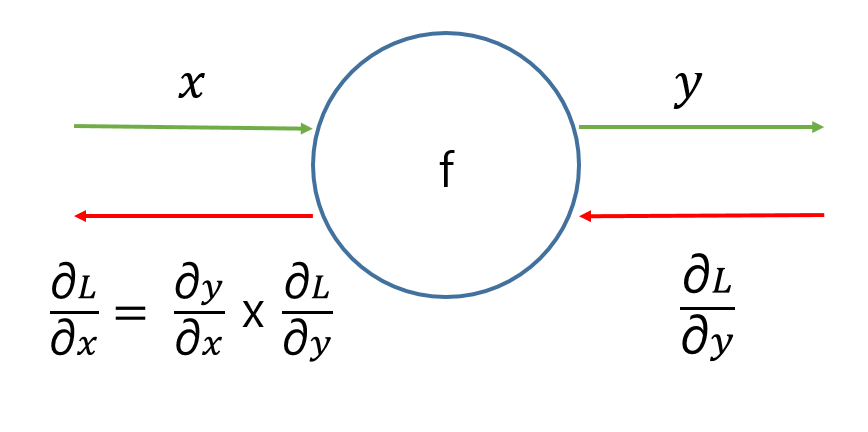
아래 그림은 간단한 ChainRule과 계산그래프를 나타내는 이미지이다.

표현 방식	의미
Node	함수
Edge	값
초록선	순전파(forward propagation)
빨간선	역전파(backward propagation)

위의 그림을 참조하게 되면
순전파(forward propagation)은 입력값 x 가 함수 f 를 거쳐 나온 값 y 로 순전하는 것을 의미한다.
역전파(backward propagation)은 출력값 L(Loss Function)을 통하여 x , y를 Update시키는 과정 이다.
역전파(backward propagation)의 경우 최종적인 결과인 Loss로부터 최초 입력 값인 x로서 순전파와 반대 방향으로 진행되므로 역전파라고 불린다.
위의 그림에서는 최종적으로 값을 바꾸어야 하는 Parameter는 x, y 라는 것을 알 수 있다.

1. y의 값을 Update하기 위해서 Loss의 값으로부터 y값이 어떻게 변할지 알아야 하므로 y에 대한 Loss의 변화량을 알아야 한다.
   y에 대한 Loss의 변화량은 \(\frac{\partial L}{\partial y}\)로서 나타내게 된다.
2. x의 값을 Update하기 위해서 Loss의 값으로부터 x값이 어떻게 변할지 알아야 하므로 x에 대한 Loss의 변화량을 알아야 한다.
   x에 대한 Loss의 변화량은 \(\frac{\partial L}{\partial x}\)로서 나타내게 된다.
   여기서 문제는 만약 Loss 함수가 MSE라고 가정하게 되면 \(L = \frac{1}{2}(y-y\prime)^{2}\) 이 되게 되고 이러한 \(L\) 은 x값으로 미분을 할 수 없게 된다.
   여기서 Chain Rule을 사용하게 되면 아래와 같이 식을 바꾸어 사용할 수 있다.

$$\frac{\partial L}{\partial x} = \frac{\partial y}{\partial x} \frac{\partial L}{\partial y}$$

위와 같이 식이 바뀌게 되어 y는 x에 대한 함수, Loss 는 y에 대한 함수이므로 각각 미분 가능하여 값을 계산 할 수 있다.

Backpropagation

아래와 그림과 같이 간단한 하나의 신경을 생각해 보자.

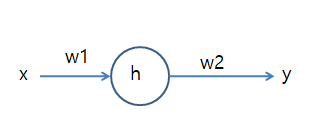
위와 같은 신경에 대한 Cost Function을 MSE를 사용하면 Cost Function은 아래와 같은 식으로 표현할 수 있다.

$$C=\frac{1}{2}(y-y\prime)^{2}$$

Weight를 Update하기 위하여 Gradient Decent를 사용하게 되면 W2에 대한 식은 아래와 같은 식으로 표현할 수 있다.

$$W_2(Update)=W_2-\alpha\frac{\partial C}{\partial W_2}$$

예측한 값인 \(y\prime\) 은 결국 0 혹은 1로써 표현되는 상수이므로 아래와 같은 식을 유도할 수 있다.

$$\frac{\partial C}{\partial W_2} = $$

$$(y-y\prime) \frac{\partial y}{\partial W_2} =$$

$$(y-y\prime) \frac{\partial}{\partial W_2}g(W_2h)$$

(g(x): Sigmoid Function)

Sigmoid 함수를 미분하게 되면 \(g\prime(x) = g(x)(1-g(x))\) 이다.
또한 \(g(x) = y(1-y)\) 이다.(Sigmoid는 0 또는 1의 값을 가지는 함수 이므로)

위의 식과 Chain Rule을 사용하게 되면 아래와 같은 식을 얻을 수 있다.

$$\frac{\partial C}{\partial W_2} = $$

$$(y-y\prime)g(W_2h)(1-g(W_2h)) \frac{\partial W_2h}{\partial W_2} = $$

$$(y-y\prime)y(1-y) \frac{\partial W_2h}{\partial W_2} = $$

$$(y-y\prime)y(1-y)h$$

Weight2를 Update하였으므로 W1에 대한 식을 위와같은 과정을 거치게되면 아래와 같은 식으로 표현할 수 있다.

$$\frac{\partial C}{\partial W_1} = $$

$$(y-y\prime) \frac{\partial y}{\partial W_1} = $$

$$(y-y\prime) \frac{\partial}{\partial W_1} = $$

$$(y-y\prime)g(w_2h)(1-g(w_2h)) \frac{\partial W_2h}{\partial W_1} = $$

$$(y-y\prime)y(1-y) \frac{\partial W_2h}{\partial W_1} = $$

$$(y-y\prime)y(1-y)W_2 \frac{\partial h}{\partial W_1} = $$

$$(y-y\prime)y(1-y)W_2 \frac{\partial}{\partial W_1}g(W_1x) = $$

$$(y-y\prime)y(1-y)W_2h(1-h) \frac{\partial W_1x}{\partial W_1} = $$

$$(y-y\prime)y(1-y)W_2h(1-h)x = $$

$$(y-y\prime)y(1-y)h(1-h)W_2x$$

최종적인 식 2개를 비교하게 되면

$$(y-y\prime)y(1-y)h$$

$$(y-y\prime)y(1-y)h(1-h)W_2x$$

으로서 겹치는 부분 \((y-y\prime)y(1-y)h\)가 겹치게 된다.
또한

$$(y-y\prime)y(1-y)h = \delta_y$$

$$(y-y\prime)y(1-y)h(1-h)W_2 = \delta_h$$

라 치환을 하게 되면 \(\delta_{h} = \delta_{y}g\prime (x)W_2\)로서 표현할 수 있다.
위의 결과를 얻어서 아래와 같이 Hidden Layer가 3개인 층인 망을 아래와 같이 생각해보자.

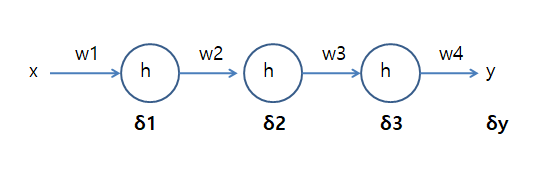
위와 같은 그림일때 위에서 증명한 수식을 사용하게 되면 아래와 같은 식을 알 수 있다.

$$\delta3 = \delta yg\prime(x) W_4$$

$$\delta2 = \delta 3g\prime(x) W_3$$

$$\delta1 = \delta 2g\prime(x) W_2$$

위와 같이 처음 \(\delta y\) 를 알게되면 나머지의 값을 쉽게 구할 수 있다.
이렇게 Weight의 Update는 BackPropagation으로 진행되면서 Update가 된다.

---

참조: Chanwoo Timothy Lee Youtube
참조: Nenyaffle 블로그
문제가 있거나 궁금한 점이 있으면 wjddyd66@naver.com으로 Mail을 남겨주세요.