NeuralNetwork (5) 학습 관련 기술들

가중치의 초깃값

가중치의 초기값을 무엇으로 설정 하느냐가 신경망 학습의 결과에 많은 영향을 미치기 때문에 가중치의 초기값을 어떻게 설정하는 지에 대하여 알아보자.
초기값을 0으로 선언
가중치의 초기값을 0으로 선언하였을때 결과를 생각해보자.
초기값을 모두 0으로 해서는 Backpropagation에서 모든 가중치의 값이 똑같이 갱신된다.
먼저 덧셈 연산이나 곱셈 연산의 경우 어떠한 연산을 하여도 전달하는 값을 Parameter가 모두 같거나 0으로 죽어버리는 현상이 발생하게 된다.

초기값을 0이 아닌 경우 초기 값이 0이 아닌 경우 아래와 같은 공통된 상황에서 가중치의 초기값에 따른 활성화값의 분포를 살펴보자.
먼저 공통된 상황에 대하여 살펴보자.

• 뉴런: 100개
• 입력 데이터: 1000개의 데이터를 정규분포로 무작위로 생성
• 활성화 함수: 시그모이드 함수

def sigmoid(x):
    return 1 / (1 + np.exp(-x))


def ReLU(x):
    return np.maximum(0, x)


def tanh(x):
    return np.tanh(x)
    
input_data = np.random.randn(1000, 100)  # 1000개의 데이터
node_num = 100  # 각 은닉층의 노드(뉴런) 수
hidden_layer_size = 5  # 은닉층이 5개
activations = {}  # 이곳에 활성화 결과를 저장

x = input_data

for i in range(hidden_layer_size):
    if i != 0:
        x = activations[i-1]

    # 초깃값을 다양하게 바꿔가며 실험해보자！
    w = np.random.randn(node_num, node_num) * 1
    # w = np.random.randn(node_num, node_num) * 0.01
    # w = np.random.randn(node_num, node_num) * np.sqrt(1.0 / node_num)
    # w = np.random.randn(node_num, node_num) * np.sqrt(2.0 / node_num)


    a = np.dot(x, w)


    # 활성화 함수도 바꿔가며 실험해보자！
    z = sigmoid(a)
    # z = ReLU(a)
    # z = tanh(a)

    activations[i] = z

# 히스토그램 그리기
for i, a in activations.items():
    plt.subplot(1, len(activations), i+1)
    plt.title(str(i+1) + "-layer")
    if i != 0: plt.yticks([], [])
    # plt.xlim(0.1, 1)
    # plt.ylim(0, 7000)
    plt.hist(a.flatten(), 30, range=(0,1))
plt.show()

위의 공통적인 조건을 가지고 가중치의 초기값만 바꾸면서 Histogram을 그려서 가중치의 값을 확인하여 보자.

1. 표준편차가 1인 경우(w = np.random.randn(node_num, node_num) * 1)

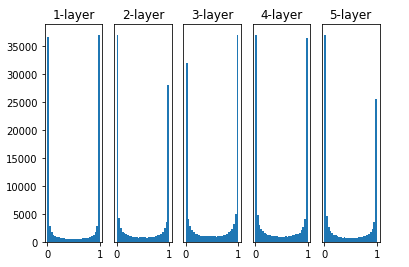
Activation Function을 Sigmoid를 사용하였다.
Sigmoid를 사용하면 -5보다 5보다 클 경우 Gradient값이 지나치게 작아지는 단점을 가지고 있다.
즉, WX의 값이 클 경우 가중치의 초기값이 클 경우 1 혹은 0으로서 극단적인 값에 집중적으로 치우치게 되는 현상이 발생하게 된다.
이러한 0 혹은 1에 Activation Function의 값이 집중적으로 치우치는 현상이 발생하게 되면 SIgmoid의 미분식을 살펴보았을때 y(1-y)식에서 y에 0 혹은 1을 대입하게 되어서 BackPropagation의 기울기 값이 점점 작아지다가 사라지게 되는 Gradient Vanishing이 발생하게 된다.

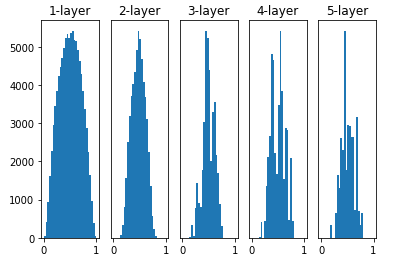
2. 표준편차가 0.01인 경우(w = np.random.randn(node_num, node_num) * 0.01)

즉, WX의 값이 작은 경우 Activation Function을 거쳐 결과값이 일정한 값으로 수렴해서 계속해서 나오는 현상이 발생
Activation Function의 일정한 한값에 집중적으로 치우치는 현상이 발생하게 되면 표현력을 제한하는 관점에서 문제가 생기게 된다.
즉 다수의 뉴런이 거의 같은 값을 출력하고 있으니 뉴런을 여러 개 둔 의미가 사라지게 된다는 의미이다.

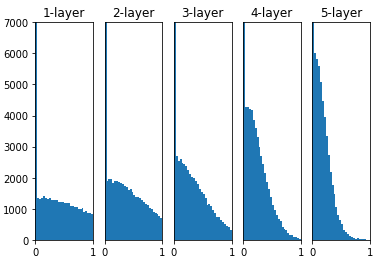
3. Xavier(w = np.random.randn(node_num, node_num) * np.sqrt(node_num))

Xavier Glorot & Yoshua Bengio의 논문에서 권장하는 가중치의 초기값이다.
앞 층의 입력 노드 수에 더하여 다음 계층의 출력 노드 수를 함께 고려하여 초기값을 설정하는 방법이다.
위의 그림에서 살펴보았듯이 Activation Function의 결과 값이 골고루 분포하게 되여 표현력의 제한 이나 Gradient Vanishing문제를 해결한 것을 볼 수 있다.

Activation ReLU
sigmoid 와 tanh함수는 좌우 대칭인 함수이다.
하지만 ReLU는 0이상의 값은 그대로이고 0이하의 값은 모두 0으로 출력값을 출력하기 때문에 ReLU는 Xavier가 아닌 다른 초기값을 추천한다.
ReLu를 Activation Function으로서 사용할 경우 He 초기값을 추천한다.
Xavier

$$ \sqrt{\frac{1}{n}} $$

He:

$$ \sqrt{\frac{2}{n}} $$

아래 결과는 각각의 가중치를 어떻게 초기화 하였는지에 대한 결과 값이다.

std = 0.01

Xavier

He

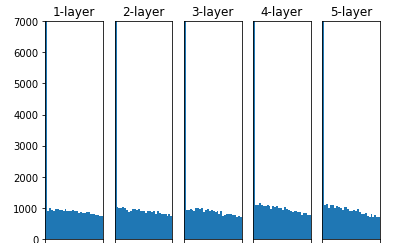
배치 정규화

배치 정규화는 효율을 높이기 위해 도입되었다. 배치 정규화는 Regularization을 해준다고 이해할 수 있다. 배치 정규화를 사용하면 다음과 같은 이점이 발생하게 된다.

1. 학습을 빨리 진행할 수 있다.(학습 속도 개선)
2. 초깃값에 크게 의존하지 않는다.
3. 오버피팅을 억제한다.

배치 정규화는 활성함수의 활성화값 또는 출력값을 정규화 하는 작업을 의미한다. 이는 데이터 분포가 치우치는 현상을 해결함으로써 가중치가 엉뚱한 방향으로 갱신될 문제를 해결할 수 있다.

배치 정규화의 과정은 아래와 같은 그림으로 나타낼 수 있다.

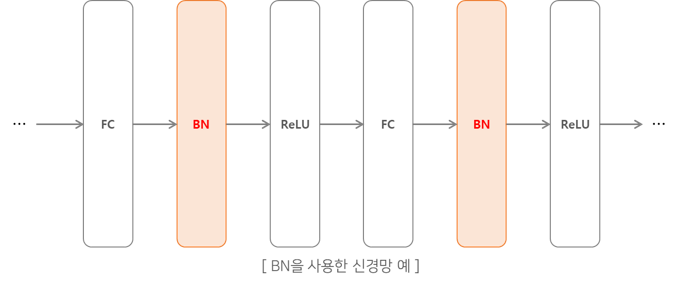
위의 그림으로서 데이터의 분포가 평균이 0, 분산이 1이 되도록 정규화를 한다.
수식으로는 아래와 같이 나타낼 수 있다.

$$ \mu_B \leftarrow \frac{1}{m}\sum_{i=1}^m x_i$$

$$ \sigma_B^2 \leftarrow \frac{1}{m}\sum_{i=1}^m (x_i-\mu_B)^2$$

$$ \hat{x_i} \leftarrow \frac{x_i-\mu_B}{\sqrt{\sigma_B^2 + \varepsilon}}$$

$$ B = {x_1, x_2, ... , x_m} $$

위의 식에서 알 수 있듯이 m개의 입력 데이터의 집합에 대해 평균 \(\mu_B\)와 분산\(\sigma_B^2\)를 구한다.
그리고 입력 데이터를 평균이 0, 분산이 1이 되게 정규화를 실시한다.
\(\varepsilon\)는 매우 작은 값으로서 \(\frac{x_i-\mu_B}{\sqrt{\sigma_B^2 + \varepsilon}}\)의 값이 inf가 되는 것을 방지한다.

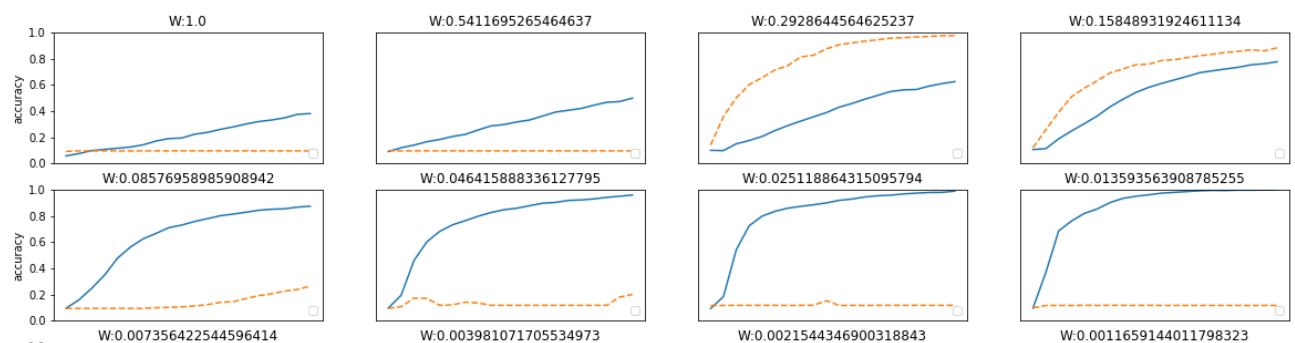
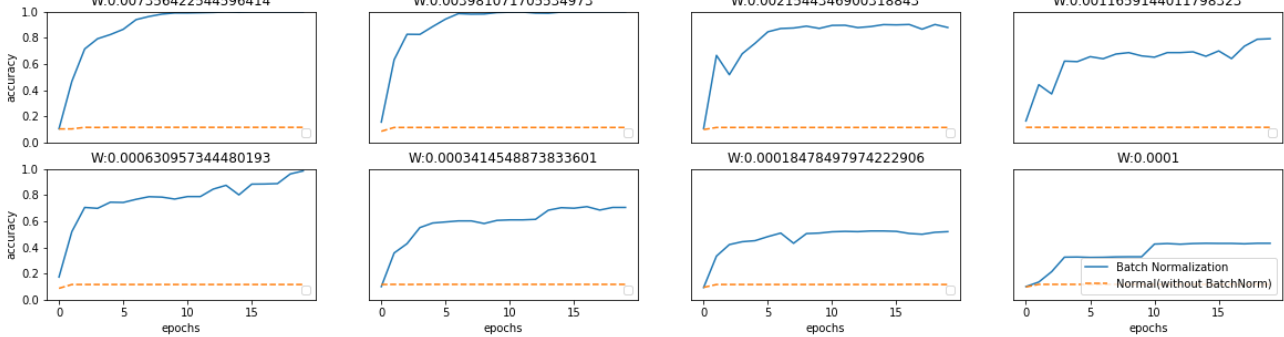
거의 모든 경우에서 배치 정규화를 사용할 때의 학습 진도가 빠른것을 나타낸다.
배치 정규화를 이용하지 않는 경우엔 초깃값이 잘 붙포되어 있지 않으면 학습이 진행되지 않는 모습도 확인할 수 있다.

오버피팅과 언터피팅

아래 그림은 오버피팅과 언더피팅에 대한 그림이다.

위의 그림을 살펴보게 되면 오버피팅과 언더피팅을 정의할 수 있다.
Underfitting: 합습 오차가 큰 경우
Overfitting: 학습 오차는 작은데 테스트 오차가 큰 경우

위와 같은 Overfitting과 Underfitting을 수식으로서 알아보면 다음과 같다.

• x: Input Data
• t: Target Data
• f: Model
• ϵ: Noise

위와 같이 Parameter가 정의되어 있으면 Target Data는 아래처럼 표현 할 수 있다.
\(t = f(x) + ϵ\)

Loss Function을 MSE로서 사용하여 되면 Loss의 기대값은 Loss Function을 MSE로서 사용하여 되면 Loss의 기대값은\(E\{(t-y)^2\}\) 으로서 표현 할 수 있다.
Loss Function을 조금 더 풀어보면 다음과 같다.

\(E\{(t-y)^2\} = E\{(t-f+f-y)^2\}\) \(= E\{(t-f)^2\} + E\{(f-y)^2\} + 2E\{(f-y)(t-f)\}\) \(= E\{ϵ^2\} + E\{(f-y)^2\} + 2[E\{ft\} - E\{f^2\} - E\{yt\} + E\{yf\}]\) \(= E\{(f - E\{y\} + E\{y\} - y)^2\} + E\{ϵ^2\}\)
\((\because t = f + ϵ 이므로 ft - f^2 - yt + yf\) \(f(f + ϵ) - f^2 - y(f + ϵ) + yf = fϵ - yϵ = 0)\)
\(= E\{(f-E\{y\})^2\} + E\{(E\{y\}-y)^2\} + 2E\{(E\{y\}-y)(f-E\{y\})\} + E\{ϵ^2\}\) \(= E\{(f-E\{y\})^2\} + E\{(E\{y\}-y)^2\} + E\{ϵ^2\}\)
\((\because 2E\{(E\{y\}-y)(f-E\{y\})\} =0 )\)

최종적인 식을 살펴보게 되면 각각을 의미하는 것은 다음과 같다.

• \(E\{(f-E\{y\})^2\}\) : Bias(편차)의 제곱
• \(E\{(E\{y\}-y)^2\}\) : Variance(분산)
• \(E\{ϵ^2\}\) : Noise

최종적인 식에서 \(E\{ϵ^2\}\) 은 독립적인 값이므로 최소화를 할 수 없으므로 Bias의 제곱과, Variance가 최소가 되는 Model을 찾는것이 결국 목표이다.

각각의 Variance와 Bias에 따른 예측값의 분포를 살펴보면 다음 그림과 같다.

위의 그림으로서 살펴보게 되면 결론적으로 Overfitting과 Underfitting은 다음과 같은 현상일 때 나타난다.
Overfitting은 분산은 작으나 편차가 클 경우 발생(High Bias)
Underfitting은 분산이 큰 경우 발생(High Variance)
조금 더 직관적으로 살펴보면 다음과 같은 사진으서 생각할 수 있다.

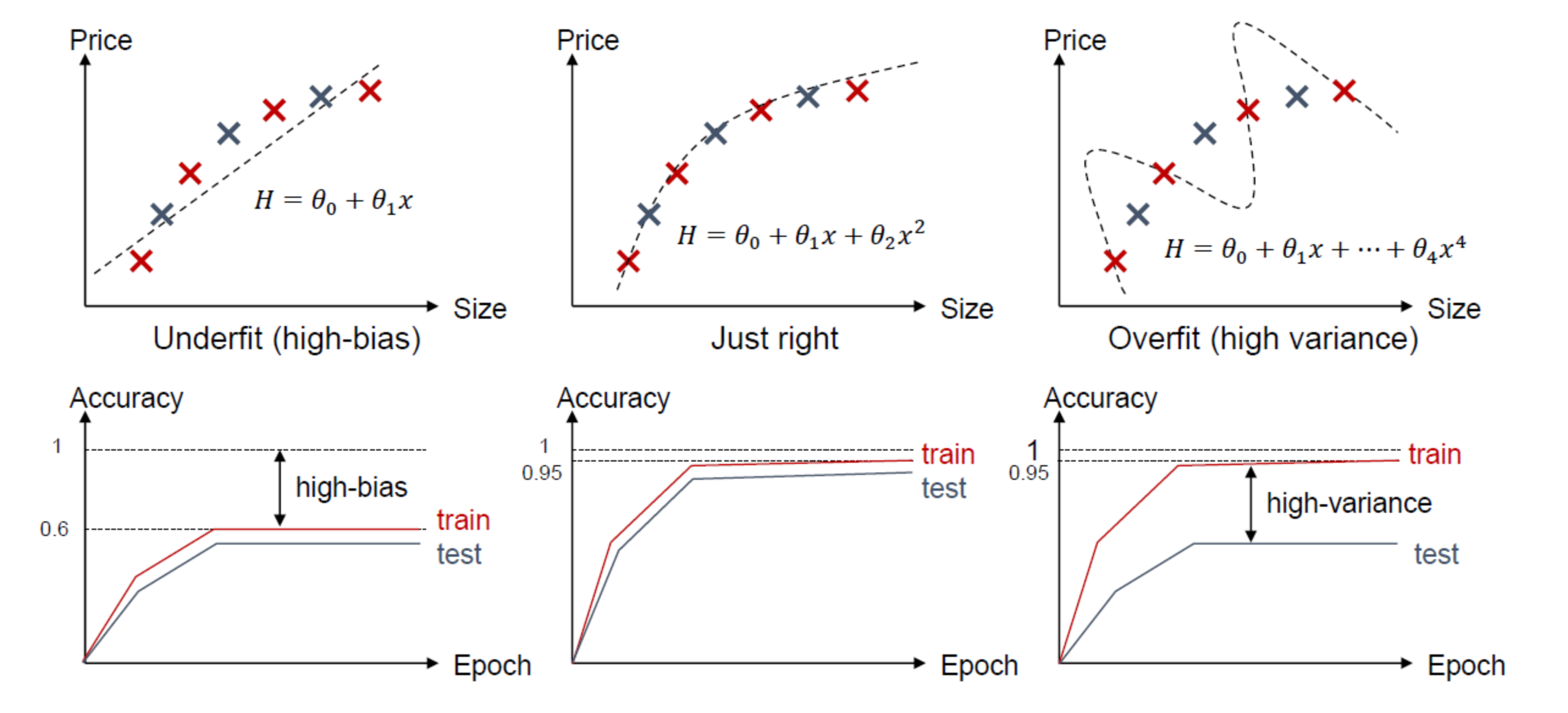
위에서 말하는 분산은 Model에 적용시키면 Feature라고 할 수 있다.
아래 그림은 Feature에 따른 Underfit과 Overfit에 관한 그림이다.

위의 그림에서도 알 수 있듯이 적정수의 Feature의 수가 Model에서 Underfitting과 Overfitting을 안일어나게 할 수 있다.
이러한 Overfitting된 Model의 결과를 보게 되면 아래그림과 같다.

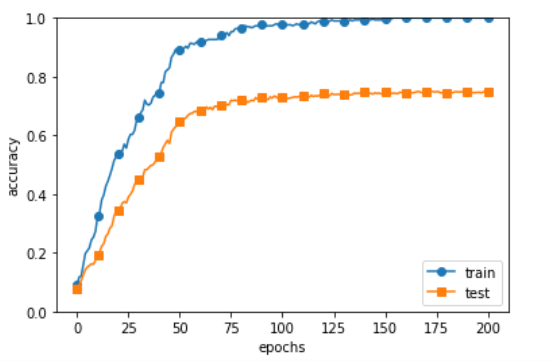
Train Data에 대한 결과 예측력은 매우 높지만 새로운 데이터인 Test Data에 대한 결과 예측은 안좋은 모습을 보이는 것을 확인 할 수 있다.

이러한 Overfitting 방지 방법으로는 대표적으로 2가지가 존재하게 된다.

1. 가중치감소
가중치 감소란 학습 과정에서 큰 가중치에 대해서는 그에 상응하는 큰 패널티를 부과하여 오버피팅을 억제하는 방법이다.
매우 큰 가중치가 존재한다고 생각하면 그 하나의 가중치에 의해서 Model이 결정되므로 Overfitting된다고 생각할 수 있기 때문이다.
이러한 가중치 감소는 크게 2가지로 나뉘어 질 수 있다.
1) L2 Regularization: 가장 일반적인 regulization 기법입니다. 기존 손실함수(Lold)에 모든 학습파라메터의 제곱을 더한 식을 새로운 손실함수로 씁니다. 아래 식과 같습니다. 여기에서 1/2이 붙은 것은 미분 편의성을 고려한 것이고, λ는 패널티의 세기를 결정하는 사용자 지정 하이퍼파라메터입니다. 이 기법은 큰 값이 많이 존재하는 가중치에 제약을 주고, 가중치 값을 가능한 널리 퍼지도록 하는 효과를 냅니다.

$$W = [w_1, w_2, ... , w_n]$$

$$L_{new} = L_{old} + \frac{\lambda}{2}(w_1^2 + w_2^2 + ... + w_n^2)$$

2) L1 Regularization: 기존 손실함수에 학습파라메터의 절대값을 더해 적용합니다. 이 기법은 학습파라메터를 sparse하게(거의 0에 가깝게) 만드는 특성이 있습니다.

$$L_{new} = L_{old} + \lambda (\left| w_1 \right| + \left| w_2 \right| + ... + \left| w_n \right|)$$

각각의 방식을 그래프로 표현하게 되면 다음과 같다.

즉, L1 Regularization에서 Sparse하다는 것은 Weight가 0으로 될 확률이 높다는 것이다.
Sparse: 전체 w중 0이 많은 경우
위의 공통된 식을 살펴보게 되면 가중치가 큰 곳에 더 큰 Loss를 더해주는 것이 핵심이다.
Loss 가 커지게 되면 Gradinet Descent 를 생각하였을 때 더욱 더 빨리 최소값에 수렴하게 되고 빨리 수렴하게 되면 무한정으로 커지는 것을 막을 수 있다.
아래 그림은 가중치 감소를 적용하였을때의 그래프 이다.

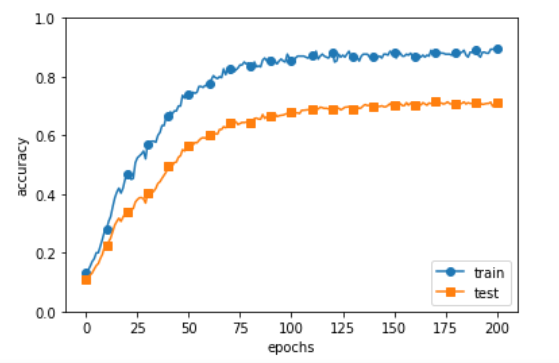
2. DropOut Dropout은 Overfitting을 막기위한 방법으로 뉴럴 네트워크가 학습중일때, 랜덤하게 뉴런을 꺼서 학습함으로써, 학습이 학습용 데이터로 치우치는 현상을 막아준다.

그림출처:leonardoaraujosantos

위와 같은 DeopOut은 아래의 코드로서 간단히 구현 될 수 있다.

class Dropout:
    def __init__(self, dropout_ratio=0.5):
        self.dropout_ratio = dropout_ratio
        self.mask = None
    
    def forward(self, x, train_flg=True):
        if train_flg:
            self.mask = np.random.rand(*x.shape) > self.dropout_ratio
            return x * self.mask
        else:
            return x * (1.0 - self.dropout_ratio)
    
    def backward(self,dout):
        return dout * self.mask

여기서 주목해야 하는 점은 훈련 시에는 순전파 때마다 self.mask에 삭제할 뉴런을 False로 표시하는 것이다.
또한 순전파 때 신호를 통과시키는 뉴런은 역전파 때도 신호를 그대로 통과시키고, 순전파 때 통과시키지 않은 뉴런은 역전파 때도 신호를 차단한다.
아래 그림은 가중치 감소를 적용하였을때의 그래프 이다.

이러한 Dropout기법은 앙상블 기법이라고도 불리게 된다.
앙상블 학습은 개별적으로 학습시킨 여러 모델의 출력을 평균을 내어 추론하는 방식이다.

적절한 하이퍼파라미터 값 찾기

기본적인 신경망에는 하이퍼파라미터가 다수 등장한다.
하이퍼파라미터란 뉴런 수, 배치 크기, 매개변수 갱신 시의 학습률과 가중치 감소등 신경망에서 정해져있는 값이 아닌 사용자가 직접 값을 넣어야 하는 변수를 의미한다.
이러한 하이퍼파라미터의 값이 매우 중요하지만 그 값을 결정하기까지는 일반적으로 많은 시도를 통하여 찾는 방법밖에 없다.
이러한 하이퍼파라미터의 값을 최대한 효율적으로 탐색하는 방법을 알아보자.

이전까지의 우리는 Dataset을 Train Data와 Test Data로서 2가지로 나누었다.
이러한 방식의 단점으로는 오버피팅등 문제점에 대한 자세한 학습이 진행되는지를 알 수 없다는 것 이다.
이러한 문제점을 검증하기 위한 Dataset을 Validation Data라고 부르게 된다.

• Train Data: 매개변수 학습
• Validation Data: 하이퍼파라미터 성능 평가
• Test Data: 신경망의 범용 성능 평가

이러한 Validation Data를 구축할 때 주의해야 하는 점은 Test Data를 사용해서는 안된다는 것 이다.
이러한 Test Data로서 Validation Data를 구축하게 되면 Test Data에 대해서 Overfitting 될 수 있는 위험성이 존재하기 때문이다.

하이퍼파라미터 최적화
하이퍼 파라미터를 최적화할 때의 핵심은 하이퍼파라미터의 최적값이 존재하는 범위를 조금씩 줄여간다는 것 이다. 범위를 조금씩 줄이려면 우선 대략적인 범위를 설정하고 그 범위에서 무작위로 하이퍼파라미터 값을 골라낸 후 , 그 값으로 정확도를 평가한다.
정확도를 살피는 작업을 여러 번 반복하며 하이퍼파라미터의 최적값 범위를 좁혀가는 것 이다.
이러한 대략적인 범위는 10의 거듭제곱 단위를 범위로 지정하는 것이 일반적이고 학습의 에폭을 작게 하여, 1회 평가에 걸리는 시간을 단축하는 것이 효과적 이다.

하이퍼 파라미터 최적화 과정

1. 하이퍼파라미터 값의 범위를 설정(10의 거듭제곱 단위를 범위로 지정하는 것이 일반적)
2. 설정된 범위에서 하이퍼파라미터의 값을 무작위로 추출
3. 2단계에서 샘플링한 하이퍼파라미터 값을 사용하고, 검증 데이터로 정확도를 평가(에폭은 작게하여 1회 평가에 걸리는 시간을 단축하는 것이 효과적)
4. 2단계와 3단계를 특정 횟수 반복하여, 그 정확도의 결과를 보고 하이퍼파라미터의 범위를 좁힌다.

위의 그림으로서는 가중치 감소 계수의 범위를 \(10^{-8}\) ~ \(10^{-4}\), 학습률의 범위를 \(10^{-6}\) ~ \(10^{-2}\)로 하여 실험한 결과이다.

위의 그림에 대한 Best5를 뽑게되면 아래와 같다.

Best-1(val acc:0.83) | lr:0.009098028051193552, weight decay:3.1204748491733006e-08
Best-2(val acc:0.78) | lr:0.007950676856659285, weight decay:7.290196504465358e-08
Best-3(val acc:0.78) | lr:0.008838720739838171, weight decay:1.946596595144894e-07
Best-4(val acc:0.78) | lr:0.008843900851177939, weight decay:3.7740789968164674e-06
Best-5(val acc:0.77) | lr:0.008334498605369918, weight decay:4.621838061557274e-07

개인적인 경험에 의해서는 가장 최선의 하이퍼파라미터 하나만 가지고 Trainning 하는 과정을 거치는 것 보다 상위 몇개의 하이퍼파라미터로서 Trainning 후 결과가 좋은 것을 사용하는 것이 Model의 성능을 향상 시킬 수 있는 방법이였다.

---

참조:원본코드
참조:ratsgo’s 블로그
참조: sacko 블로그
참조: untitledtblog 블로그
참조: nittaku 블로그
참조: 밑바닥부터 시작하는 딥러닝
문제가 있거나 궁금한 점이 있으면 wjddyd66@naver.com으로 Mail을 남겨주세요.