Perceptron

Perceptron

Perceptron은 다수의 신호(Input)을 입력받아서 하나의 신호(Output)을 출력한다. 이는 뉴런이 전기신호를 내보내 정보를 전달하는 것과 비슷하다.
뉴런의 신호전달하는 역할을 Perceptron에서는 weight
신호의 총합이 정해진 입계값(\(\theta: 세타\) )를 넘었을때 1을 출력한다.

그림출처Jia-Bin Huang PPT

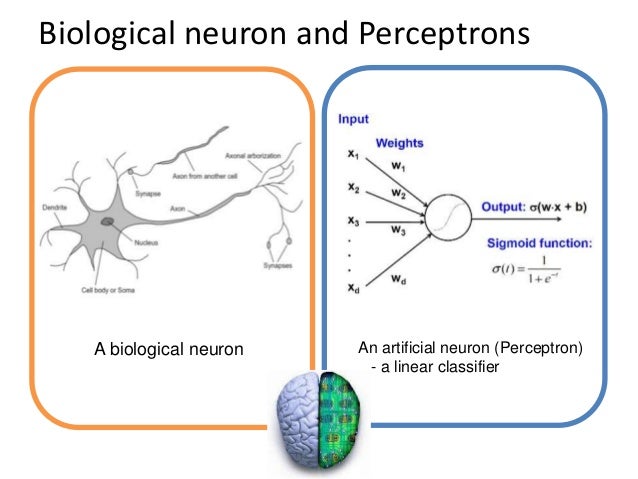
실제 값	용어
x1, x2, ..., xd	Input(입력)
w1, w2, ..., wd	Weight(가중치)
y	Output(출력)
b	bias(편향)
$$ \sigma $$	Activatation Function(활성화 함수)

Activate Function(Input과 가중치를 활용하여 Output을 만들어내기 위한 식)이 Sigmoid를 사용하므로 최종적인 Output의 식은 아래와 같다.

$$ y = {1 \over 1+e^{-\sum_{i=0}^d w_ix_i + b}}$$

최종적으로 우리는 위의 식에 대입한 값이 \(\theta\) 를 넘으면 1, 넘지 못하면 0으로서 판단할 수 있게 된다.
실제 y와 x는 주어진 Data이므로 우리가 중점적으로 봐야할 것은 weight 와 bias 이다.
적절한 weight 와 bias 를 조정하기 위한 과정이 반복적으로 이루어지게 되고 우리는 이러한 것을 ‘Model을 Trainning 한다’ 라고 표현한다.
이러한 Trainning 하여 알아내야 되는 변수의 의미를 살펴보면 아래와 같다.
가중치(weight)는 입력신호가 결과 출력에 주는 영향도를 조절하는 매개변수이고, 편향(bias)은 뉴런(또는 노드; x를 의미)이 얼마나 쉽게 활성화(1로 출력; activation)되느냐를 조정하는(adjust) 매개변수이다.

Perceptron의 한계점과 극복

Perceptron의 한계점으로는 선형분류만 가능하다는 것이다.
XOR과 같이 선형분류가 아닌 exclusive 논리연산은 분류할 수 없다는 문제가 생기게 된다.

그림출처ecee.colorado.edu
AND Gate 진리표

X1	X2	Y
0	0	0
0	1	0
1	0	0
1	1	1

AND Gate 구현

#AND
def AND(x1,x2):
    x = np.array([x1,x2])
    w = np.array([0.5,0.5])
    b = -0.7
    tmp = np.sum(w*x) + b
    if tmp<0:
        return 0
    else:
        return 1

AND Gate 결과 확인

#AND 확인
print(AND(0,0))
print(AND(0,1))
print(AND(1,0))
print(AND(1,1))

0
0
0
1

OR Gate 진리표

X1	X2	Y
0	0	0
0	1	1
1	0	1
1	1	1

OR Gate 구현

#OR
def OR(x1,x2):
    x = np.array([x1,x2])
    w = np.array([0.5,0.5])
    b = -0.2
    tmp = np.sum(w*x) + b
    if tmp<0:
        return 0
    else:
        return 1

OR Gate 결과 확인

#OR 확인
print(OR(0,0))
print(OR(0,1))
print(OR(1,0))
print(OR(1,1))

0
1
1
1

위와 같이 선형분류만 가능하다는 한계점을 극복하기 위하여 다층 퍼셉트론을 이용하여 한계를 극복하였다.
다층 Perceptron이란 여러개의 Perceptron으로 인하여 비선형 영역을 분리할 수 없다는 한계를 해결한 것이다.

그림출처ecee.colorado.edu

XOR Gate 진리표

X1	X2	Y
0	0	0
0	1	1
1	0	1
1	1	0

XOR Gate 구현

#MLP
#XOR
def XOR(x1,x2):
    s1 = lambda x1,x2:1 if AND(x1,x2) == 0 else 0
    s2 = OR(x1,x2)
    y = AND(s1(x1,x2),s2)
    return y

XOR Gate 결과 확인

#XOR 확인
print(XOR(0,0))
print(XOR(0,1))
print(XOR(1,0))
print(XOR(1,1))

0
1
1
0

---

참조: 원본코드
문제가 있거나 궁금한 점이 있으면 wjddyd66@naver.com으로 Mail을 남겨주세요.