Ch1.The Machine Learning Landscape

8 minute read

Ch1. The Machine Learning Landscape

이번 Chapter에서는 간단한 Machine Learning의 Flow에 대하여 살펴보자.

기본적으로 필요한 Library들은 pip install -r requirements.txt로서 설치할 수 있다.

필요한 Library Import

%matplotlib inline
import matplotlib as mpl
import matplotlib.pyplot as plt
import urllib


import os
import sys

import numpy as np
import pandas as pd
import sklearn
import sklearn.linear_model
from sklearn import preprocessing
from sklearn import pipeline

import tensorflow as tf

# Matplotlib Setting
mpl.rc('axes', labelsize=14)
mpl.rc('xtick', labelsize=12)
mpl.rc('ytick', labelsize=12)

Library Version Check

# Python ≥3.5 is required
assert sys.version_info >= (3, 5)

# Scikit-Learn ≥0.20 is required
assert sklearn.__version__ >= "0.20"

# Tensorflow Version check
print(tf.__version__)

2.0.1

Preprocessing

이미지를 저장하기 위한 Function과 Directory를 생성한다.
이번 Chapter와 앞으로의 Chapter에서도 Dataset을 Visualization하거나 결과를 확인하기 위해서 이다.
또한 항상 같은 결과를 내기 위하여 Random의 Seed또한 고정한다.

# Where to save the figures
PROJECT_ROOT_DIR = "."
CHAPTER_ID = "fundamentals"
IMAGES_PATH = os.path.join(PROJECT_ROOT_DIR, "images", CHAPTER_ID)
os.makedirs(IMAGES_PATH, exist_ok=True)

def save_fig(fig_id, tight_layout=True, fig_extension="png", resolution=300):
    path = os.path.join(IMAGES_PATH, fig_id + "." + fig_extension)
    print("Saving figure", fig_id)
    if tight_layout:
        plt.tight_layout()
    plt.savefig(path, format=fig_extension, dpi=resolution)
    
np.random.seed(42)

Dataset

기본적으로 이번 Chapter에서 사용하는 Dataset을 Download받고 확인하는 작업이다.

사용하는 Dataset은 Handson-ml2에서 Download받거나 아래 Code를 통하여 Download받는다.

# Dataset Path
datapath = os.path.join("datasets", "lifesat", "")

# Download the Dataset
DOWNLOAD_ROOT = "https://raw.githubusercontent.com/ageron/handson-ml2/master/"
os.makedirs(datapath, exist_ok=True)
for filename in ("oecd_bli_2015.csv", "gdp_per_capita.csv"):
    print("Downloading", filename)
    url = DOWNLOAD_ROOT + "datasets/lifesat/" + filename
    urllib.request.urlretrieve(url, datapath + filename)

Downloading oecd_bli_2015.csv
Downloading gdp_per_capita.csv

Preprocessing Data

실제 사용하기 위한 2개의 Dataset을 하나로 합치고 Model에 알맞는 Dataset으로서 변형하는 단계이다.
각각의 Dataset에 대한 Preprocessing의 과정이 다르다.

def prepare_country_stats(oecd_bli, gdp_per_capita)
Argument: oecd_bli, gdp_per_capita
Output: full_country_stats

oecd_bli_2015.csv: 현재 Dataset은 각가의 나라에 대하여 Feature에 따라 Value의 Type이 다르다.
TOT 의 Type을 가진 Value만 뽑아 낸다.
County는 Index, Column은 Feature(Indicator)로서 변형한다.
gdb_per_capita: 각가의 나라에 대하여 GDP per capita와 이를 어떤 단위로 표현하였는지 나타낸다.
2015 -> GDP per capita로서 Column을 변형한다.
Index를 Country로서 변형한다.
full_country_stats: 하나의 Dataset으로서 합친다. 다양한 Feature와 서로다른 GDP를 보유한 Dataest으로서 나타나게 된다. (36x30)
몇몇 Indicies를 제외하게 된다. 아마 Model의 결과를 증가시키기 위하여 Outlier를 제거하는 것으로 보인다.
최종적으로 GDP per capita, Life satisfaction의 Column만 가져오게 된다. 즉, GDP per capita가 Life satisfaction에 영향을 미치는지 알아보기 위해서 이러한 과정을 거치게 된다.

def prepare_country_stats(oecd_bli, gdp_per_capita):
    oecd_bli = oecd_bli[oecd_bli["INEQUALITY"]=="TOT"]
    oecd_bli = oecd_bli.pivot(index="Country", columns="Indicator", values="Value")
    gdp_per_capita.rename(columns={"2015": "GDP per capita"}, inplace=True)
    gdp_per_capita.set_index("Country", inplace=True)
    full_country_stats = pd.merge(left=oecd_bli, right=gdp_per_capita,
                                  left_index=True, right_index=True)
    full_country_stats.sort_values(by="GDP per capita", inplace=True)
    remove_indices = [0, 1, 6, 8, 33, 34, 35]
    keep_indices = list(set(range(36)) - set(remove_indices))
    
    return full_country_stats[["GDP per capita", 'Life satisfaction']].iloc[keep_indices], full_country_stats[["GDP per capita", 'Life satisfaction']].iloc[remove_indices]

Checking dtat

실제 사용하는 Dataset(oecd_bil_2015.csv, gdp_per_capitia.csv)를 활용하여 Preprocessing 과정을 거친 뒤, Data의 형태가 어떠한지 살펴보자.

# Load the data
oecd_bli = pd.read_csv(datapath + "oecd_bli_2015.csv", thousands=',')
gdp_per_capita = pd.read_csv(datapath + "gdp_per_capita.csv",thousands=',',delimiter='\t',
                             encoding='latin1', na_values="n/a")

# Prepare the data
sample_data, missing_data = prepare_country_stats(oecd_bli, gdp_per_capita)

# Visualization Data
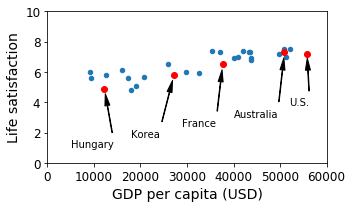
sample_data.plot(kind='scatter', x="GDP per capita", y='Life satisfaction', figsize=(5,3))
plt.axis([0, 60000, 0, 10])
position_text = {
    "Hungary": (5000, 1),
    "Korea": (18000, 1.7),
    "France": (29000, 2.4),
    "Australia": (40000, 3.0),
    "United States": (52000, 3.8),
}
for country, pos_text in position_text.items():
    pos_data_x, pos_data_y = sample_data.loc[country]
    country = "U.S." if country == "United States" else country
    plt.annotate(country, xy=(pos_data_x, pos_data_y), xytext=pos_text,
            arrowprops=dict(facecolor='black', width=0.5, shrink=0.1, headwidth=5))
    plt.plot(pos_data_x, pos_data_y, "ro")
plt.xlabel("GDP per capita (USD)")
save_fig('money_happy_scatterplot')
plt.show()

png

# Save the Dataet
sample_data.to_csv(os.path.join("datasets", "lifesat", "lifesat.csv"))

# Check the Dataset
sample_data.loc[list(position_text.keys())]

	GDP per capita	Life satisfaction
Country
Hungary	12239.894	4.9
Korea	27195.197	5.8
France	37675.006	6.5
Australia	50961.865	7.3
United States	55805.204	7.2

Linear Regression(No Train)

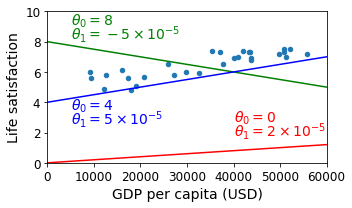
위의 Dataset을 살펴보게 되면 GDP per catita (USD)가 증가함에 따라서 Life satisfaction이 Linear하게 증가되는 것을 확인할 수 있다.

Sklearn을 사용하여 Linear Regression Model을 생성하는 것이 아닌 임의의 Parameter로서 Linear Regression을 Visualization하여 확인하여 보자.

sample_data.plot(kind='scatter', x="GDP per capita", y='Life satisfaction', figsize=(5,3))
plt.xlabel("GDP per capita (USD)")
plt.axis([0, 60000, 0, 10])
X=np.linspace(0, 60000, 1000)
plt.plot(X, 2*X/100000, "r")
plt.text(40000, 2.7, r"$\theta_0 = 0$", fontsize=14, color="r")
plt.text(40000, 1.8, r"$\theta_1 = 2 \times 10^{-5}$", fontsize=14, color="r")
plt.plot(X, 8 - 5*X/100000, "g")
plt.text(5000, 9.1, r"$\theta_0 = 8$", fontsize=14, color="g")
plt.text(5000, 8.2, r"$\theta_1 = -5 \times 10^{-5}$", fontsize=14, color="g")
plt.plot(X, 4 + 5*X/100000, "b")
plt.text(5000, 3.5, r"$\theta_0 = 4$", fontsize=14, color="b")
plt.text(5000, 2.6, r"$\theta_1 = 5 \times 10^{-5}$", fontsize=14, color="b")
save_fig('tweaking_model_params_plot')
plt.show()

png

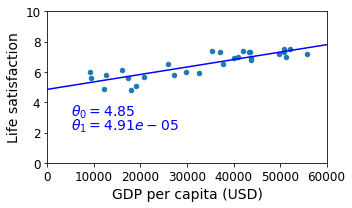
Simple Linear Regression

sklearn.linear_model을 활용하여 간단한 \(y(\text{Life satisfaction}) = \theta_1(\text{GDP per capita}) * x + \theta_0\)을 만들고 결과를 확인한다.

# Dataset
X = np.c_[sample_data["GDP per capita"]]
y = np.c_[sample_data["Life satisfaction"]]

# Select a linear model
model = sklearn.linear_model.LinearRegression()

# Train the model
model.fit(X, y)

# Get Slope and Bias
t0, t1 = model.intercept_[0], model.coef_[0][0]

# Visualization Linear Regression
sample_data.plot(kind='scatter', x="GDP per capita", y='Life satisfaction', figsize=(5,3))
plt.xlabel("GDP per capita (USD)")
plt.axis([0, 60000, 0, 10])
X=np.linspace(0, 60000, 1000)
plt.plot(X, t0 + t1*X, "b")
plt.text(5000, 3.1, r"$\theta_0 = %.2f$"%t0, fontsize=14, color="b")
plt.text(5000, 2.2, r"$\theta_1 = %.2e$"%t1, fontsize=14, color="b")
save_fig('best_fit_model_plot')
plt.show()

png

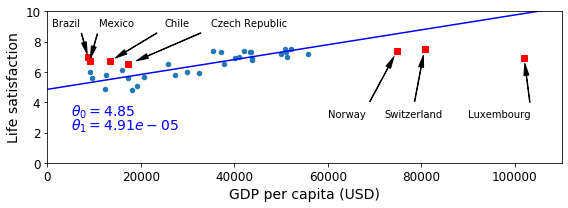
Prediction Data

실제 Train에 사용되지 않고 제외되었던 Data를 활용하여 Model의 Prediction값과 실제 값의 차이를 Visualization하여 알아보자.

missing_data

	GDP per capita	Life satisfaction
Country
Brazil	8669.998	7.0
Mexico	9009.280	6.7
Chile	13340.905	6.7
Czech Republic	17256.918	6.5
Norway	74822.106	7.4
Switzerland	80675.308	7.5
Luxembourg	101994.093	6.9

위의 Dataset은 Train에서 제외되었던 Data들이다. Training된 Model은 어떠한 값을 예측하는지 알아보자.

# Missing Data -> Dict
position_text2 = {
    "Brazil": (1000, 9.0),
    "Mexico": (11000, 9.0),
    "Chile": (25000, 9.0),
    "Czech Republic": (35000, 9.0),
    "Norway": (60000, 3),
    "Switzerland": (72000, 3.0),
    "Luxembourg": (90000, 3.0),
}

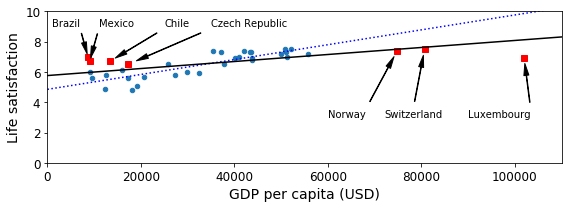
# Visualization Linear Regression
sample_data.plot(kind='scatter', x="GDP per capita", y='Life satisfaction', figsize=(8,3))
plt.xlabel("GDP per capita (USD)")
plt.axis([0, 110000, 0, 10])

# Real Data
for country, pos_text in position_text2.items():
    pos_data_x, pos_data_y = missing_data.loc[country]
    plt.annotate(country, xy=(pos_data_x, pos_data_y), xytext=pos_text,
            arrowprops=dict(facecolor='black', width=0.5, shrink=0.1, headwidth=5))
    plt.plot(pos_data_x, pos_data_y, "rs")


X=np.linspace(0, 110000, 1000)
plt.plot(X, t0 + t1*X, "b")
plt.text(5000, 3.1, r"$\theta_0 = %.2f$"%t0, fontsize=14, color="b")
plt.text(5000, 2.2, r"$\theta_1 = %.2e$"%t1, fontsize=14, color="b")
save_fig('prediction_model_plot')
plt.show()

png

ReTrain The Model

Data의 수가 적은 이유 때문에 실제 Training된 Model은 새로운 값들에 대하여 예측을 잘 못하는 경향을 보여주고 있다.
새로운 Dataset을 포함하여 Model을 Retrain시키고, 결과를 확인하여 보자.

full_country_stats = pd.concat([sample_data,missing_data])
sample_data.plot(kind='scatter', x="GDP per capita", y='Life satisfaction', figsize=(8,3))
plt.axis([0, 110000, 0, 10])

for country, pos_text in position_text2.items():
    pos_data_x, pos_data_y = missing_data.loc[country]
    plt.annotate(country, xy=(pos_data_x, pos_data_y), xytext=pos_text,
            arrowprops=dict(facecolor='black', width=0.5, shrink=0.1, headwidth=5))
    plt.plot(pos_data_x, pos_data_y, "rs")

X=np.linspace(0, 110000, 1000)
plt.plot(X, t0 + t1*X, "b:")

lin_reg_full = sklearn.linear_model.LinearRegression()
Xfull = np.c_[full_country_stats["GDP per capita"]]
yfull = np.c_[full_country_stats["Life satisfaction"]]
lin_reg_full.fit(Xfull, yfull)

t0full, t1full = lin_reg_full.intercept_[0], lin_reg_full.coef_[0][0]
X = np.linspace(0, 110000, 1000)
plt.plot(X, t0full + t1full * X, "k")
plt.xlabel("GDP per capita (USD)")

save_fig('representative_training_data_scatterplot')
plt.show()

png

Machine Learning Key Challenge

Machine Learning을 잘 Training하여 Prediction하기 위한 몇몇 중요한 과제들이 있다.

많은 양의 Dataset이 필요하다. Training을 위해서는 많은 양의 Dataset이 필요하게 되며, 많은 Dataet을 포함시킬 수록 Generalization된 Model이라고 말할 수 있다. 각각의 Model의 특성에 따라서 필요로 하는 Dataset의 양은 달라지게 된다.
대표성이 없는 훈련 데이터. 위의 과정에서 실제 Model을 Retrain하여야지 잘 Prediction할 수 있는 것을 확인하였다. 이러한 문제는 대표성이 없는 Dataset으로서 학습하였기 때문이다. 즉 Sorting된 36개의 Sample중 제외한 Index는 [0, 1, 6, 8, 33, 34, 35]이므로 매우 가난하거나 매우 부유한 곳에서의 Model의 Prediction은 결과가 매우 다른것을 확인할 수 있었다.
1) Sampling Noise: 샘플이 작으면 우연에 의하ㅏㄴ 대표성 없는 데이터가 생긴다.
2) Sampling Bias: 매우 큰 샘플도 표본 추출 방법이 잘못되면 대표성을 띠지 못할 수 있다.
낮은 품질의 데이터: Training데이터가 Error나 Outlier를 많이 포함하게 되면 Pattern을 찾기 힘들 것 이다. Preprocessing과정에서 이러한 Outlier를 제거하거나 Normalization을 통하여 줄여주는 작업이 필요하다.
관련없는 특성: Model을 Training한다는 것은 결국 Dataset에서의 Pattern을 찾는다는 의미이다. 이러한 과정에서 의미없는 Feature로서 Model을 Training하게 되면, Training결과도 좋지 않고 당연한 결과로서 Prediction도 정확하지 않은 Model이 될 것이다. 따라서 사용자에게 Feature Selection과 Feature Extraction이 매우 중요한 과정으로서 남게 된다.
Overfitting, Underfitting: Model을 다룰 때 매우 중요한 요소중 하나이다. Model의 Training정도와 Generalization을 위하여 꼭 확인해야 할 요소이다. 이번 Post에서는 양이 많아서 다루지 않는다. 궁금하신 분들은 링크를 참조하자.

Example) Overfitting 예시

full_country_stats.plot(kind='scatter', x="GDP per capita", y='Life satisfaction', figsize=(8,3))
plt.axis([0, 110000, 0, 10])

poly = preprocessing.PolynomialFeatures(degree=60, include_bias=False)
scaler = preprocessing.StandardScaler()
lin_reg2 = sklearn.linear_model.LinearRegression()

pipeline_reg = pipeline.Pipeline([('poly', poly), ('scal', scaler), ('lin', lin_reg2)])
pipeline_reg.fit(Xfull, yfull)
curve = pipeline_reg.predict(X[:, np.newaxis])
plt.plot(X, curve)
plt.xlabel("GDP per capita (USD)")
save_fig('overfitting_model_plot')
plt.show()

png

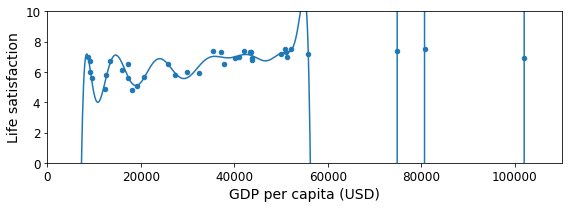
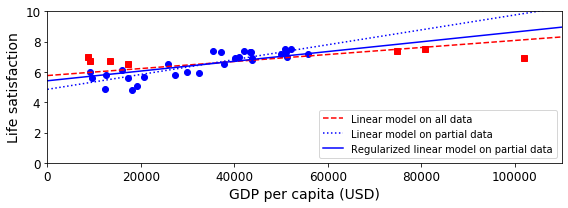
Regularization

위의 Model은 Overfitting된 Model이다.
다양한 Overfitting방지 방법이 있지만 여기에서는 L2 Regularization인 linear_model.Ridge(alpha=10**9.5)를 사용하였다.
Regularization에 대한 자세한 내용은 링크를 참조하자.

plt.figure(figsize=(8,3))

plt.xlabel("GDP per capita")
plt.ylabel('Life satisfaction')

plt.plot(list(sample_data["GDP per capita"]), list(sample_data["Life satisfaction"]), "bo")
plt.plot(list(missing_data["GDP per capita"]), list(missing_data["Life satisfaction"]), "rs")

X = np.linspace(0, 110000, 1000)
plt.plot(X, t0full + t1full * X, "r--", label="Linear model on all data")
plt.plot(X, t0 + t1*X, "b:", label="Linear model on partial data")

ridge = sklearn.linear_model.Ridge(alpha=10**9.5)
Xsample = np.c_[sample_data["GDP per capita"]]
ysample = np.c_[sample_data["Life satisfaction"]]
ridge.fit(Xsample, ysample)
t0ridge, t1ridge = ridge.intercept_[0], ridge.coef_[0][0]
plt.plot(X, t0ridge + t1ridge * X, "b", label="Regularized linear model on partial data")

plt.legend(loc="lower right")
plt.axis([0, 110000, 0, 10])
plt.xlabel("GDP per capita (USD)")
save_fig('ridge_model_plot')
plt.show()

png

참조: 원본코드
코드에 문제가 있거나 궁금한 점이 있으면 wjddyd66@naver.com으로 Mail을 남겨주세요.

Share on

Twitter Facebook LinkedIn

JeongYong Hwang

Ch1.The Machine Learning Landscape