Theory5. SVM(2)
5. SVM(2)
\(\newcommand{\argmin}{\mathop{\mathrm{argmin}}\limits}\) \(\newcommand{\argmax}{\mathop{\mathrm{argmax}}\limits}\) Machine Learning의 기초적인 이론부분을 다시 제대로 잡고 싶어서 문일철 교수님의 인공지능 및 기계학습 개론을 정리한 Post입니다.
- 5.5 Rethinking of SVM
- 5.6 Primal and Dual with KKT Condition
- 5.7 Kernel
- 5.8 SVM with Kernel
5.4 Comparison to Logistic Regression
위의 SoftMargin SVM에서 LossFunction을 Hinge Loss로서 사용하였다.
이러한 LossFunction은 이전에 배웠던 Logistic Regression에서도 사용하였다.
4.3 Logistic Regression Parameter Approximation 1에서 Logistic Regression식 을 생각해보자.
$$\hat{\theta} = \argmax_{\theta} \sum_{i=1}^N log(P(Y_i|X_i ;\theta)) = \argmax_{\theta}\sum_{i=1}^{N}(Y_iX_i\theta - log(1+e^{X_i\theta}))$$
위의 식을 살펴보게 되면 LossFunction은 \(log(1+e^{X_i\theta})\)가 되는 것을 살펴볼 수 있다.
최종적인 0-1, Hinge, Log Loss는 다음과 같이 나타낸다.
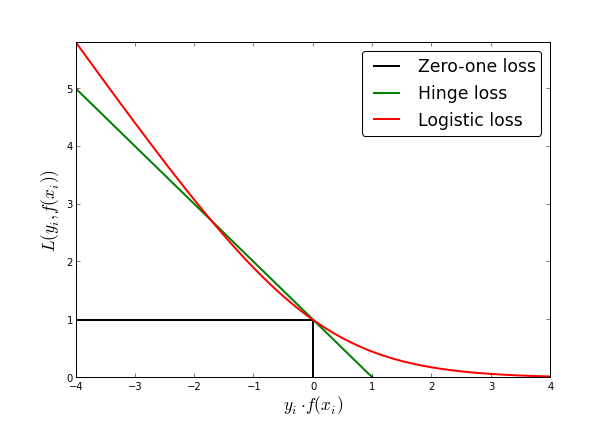
사진 출처: fa.bianp
위의 Loss를 생각해보면 다음과 같은 의미를 가지고 있다.
SVM의 경우 Hyperplane을 기준으로서 Prediction이 맞다면 Penalty가 0이다. 즉, 완벽히 Classification가능하다고 생각한다는 것 이다.
Logistic Regression의 Log Loss Function을 살펴보게 되면, 아주 잘못되어도 0이아닌 값을 가지게 된다.(0에 매우 가까울 것 이다.)즉, 아주 0에 가까운 확률로서 Prediction이 잘못되었다고 판단할 수 있다는 것 이다.
5.5 Rethinking of SVM
Kernel Trick
- Make decision boundary
- more complex
- Go to non-linear
Error를 해결하기 위하여 2번째 방법인 Kernel을 이용하는 방법이다.
Kernel하나의 예시를 식으로서 표현하면 다음과 같다.
$$\varphi(<x_1,x_2>) = <x_1, x_2, x_1^2, ..., x_1x_2^2>$$
즉, Kernel Trick이란 Data의 Dimension을 늘리는 방법이다.
Kernel Trick을 사용하기 위하여 Duality -> KKT Condition을 사용하고 이를 SVM에 적용하자.
Lagrange multiplier
$$L(x,y,\lambda) = f(x,y) - \lambda(g(x,y)-c)$$
$$\frac{\partial f}{\partial x} = \lambda \frac{\partial g}{\partial x}$$
$$\frac{\partial f}{\partial y} = \lambda \frac{\partial g}{\partial y}$$
f(x,y): Maximum지점을 찾기 위한 함수, g(x,y) = c는 조건
위의 식에서 구하고자 하는 함수와 조건을 넣으면 다음과 같이 Object Function을 얻을 수 있다.
Duality
위에서 설명한 Lagrange Multiplier를 사용하여 Primal -> Duality문제로 변형하여 보자.
얻고자 하는 것은 object Function이 Minimize되는 것 이다.
이것은 다음과 같이 나타낼 수 있다.
Step 1
$$min_{x} f(x)$$
$$\text{subject to }g(x) \le 0, h(x)=0$$
위의 식을 Largrange Multiplier를 적용하면 다음과 같이 변형할 수 있다.
$$L(x,\alpha,\beta) = f(x)+\alpha g(x) + \beta h(x)$$
만약 \(\alpha \ge 0\)이라면 아래 식이 성립하는 것을 알 수 있다.
$$f^{*} \ge min_{x \in C} L(x,\alpha,\beta) \ge min_{x} L(x,\alpha,\beta)$$
$$C: \alpha \ge 0$$: 이라는 조건이 없을 경우 x의 집합
$$f^{*}$$: 찾고자하는 Optimal 한 값
Step 2
Primal -> Duality로 변형하기 위하여 Largrange Function을 미분한다.
사용하기 위한 각각의 Function이 다음과 같을 경우
- \(f(x) = cx\)
- \(g(x) = Gx-g \le 0\)
- \(h(x) = Hx-h = 0\)
위와 같이 정리하면 식을 다음과 같이 정의할 수 있다.
$$\frac{\partial L}{\partial x}= c+\alpha G+\beta H = 0 \rightarrow c = -\alpha G -\beta H$$
위의 식을 맨 처음 Largrange Function에 대입하면 다음과 같은 결과가 나온다.
$$L(x,\alpha,\beta) = f(x)+\alpha g(x) + \beta h(x)$$
$$= (-\alpha G -\beta H)x + \alpha(Gx-g)+\beta(Hx-h) = -\alpha g - \beta h$$
위의 식은 더이상 \(x\)에 관한 식이 아닌 \(\alpha,\beta\)에 관한 식이다. 위의식 \(-\alpha g - \beta h = d(\alpha,\beta)\)라고 한다면 Largrange Function은 다음과 같다.
Step 3
$$f^{*} \ge d(\alpha,\beta)$$
위의 식이 성립하므로, Optimal한 값의 Minimize하는 것은 Duality Probelm으로 나타내었을 때 Function을 Maximize하는 것과 동일하게 된다.
즉, Primal -> Duality가 되면서 Minimize가 Maximize가 되었고, x에 관한 식이 \(\alpha,\beta\)에 관한 식으로서 변형되었다.
최종적인 식은 다음과 같다.
$$ max_{\alpha \ge 0,\beta} d(\alpha,\beta)$$
$$\text{s.t. }\alpha \ge 0$$
Duality GAP
$$f^{*} \ge min_{x \in C} L(x,\alpha,\beta) \ge min_{x} L(x,\alpha,\beta) = d(\alpha,\beta)$$
위의 식에서 항상 등호가 성립할 수는 없다.
즉, 최종적인 식(\(d(\alpha,\beta)\))은 Primal Problem에서의 Lower Boundary로서 Maximization하면 비슷한 값이 나오겠다이지, 등호가 반드시 성립은 하지 않는다. 이에 따른 실제 Optimal의 값(\(f^{*}\))과의 차이를 duality gap이라고 한다.
5.6 Primal and Dual with KKT Condition
KKT Condition이란, 이러한 Condition을 만족하는 경우 위에서 언급한 Duality Gap이 없어지고 Strong Duality이 되는 조건이다.
먼저 KKT의 조건을 살펴보면 각각 다음과 같다.
- \(\partial L(x^{*},\alpha^{*},\beta^{*}) = 0\): Lagrange Multiplier Condition
- \(\alpha^{*} \ge 0\): Primal -> Duality Condition
- \(g(x^{*}) \le 0\): Primal Condition
- \(h(x^{*}) = 0\): Primal Condition
- \(\alpha^{*}g(x^{*}) = 0\): New Condition
위의 5가지 조건에서 새롭게 추가된 조건은 5번째 조건이다.
즉, 1~4는 기존의 Primal, Duality Problem을 해결하기 위한 Condition이었고, 5번째 새로운 Condition이 추가가 되면 어떻게 KKT Condition이 성립하여 Duality Gap이 없어지는지 알아보자.
위의 Duality에서 사용한 식을 살펴보면 다음과 같다.
- \(f^{*} \ge min_{x \in C} L(x,\alpha,\beta) \ge min_{x} L(x,\alpha,\beta) = max_{\alpha \ge 0,\beta} d(\alpha,\beta)\)
- \(L(x,\alpha,\beta) = f(x)+\alpha g(x) + \beta h(x)\)
- \(f(x^{*}) = d(\alpha^{*},\beta^{*})\)(Strong Duality라면)
Duality Problem에서 전부 등호가 되기 위해서는 다음과 같은 조건이 성립하여야 한다.
$$d(\alpha^{*},\beta^{*}) = min_{x}L(x,\alpha^{*},\beta^{*}) = L(x^{*},\alpha^{*},\beta^{*}) = f(x^{*})$$
Primal Problem에서 전부 등호가 되기 위해서는 다음과 같은 조건이 성립하여야 한다.
$$L(x^{*},\alpha^{*},\beta^{*}) = f(x^{*})+\alpha^{*} g(x^{*}) + \beta^{*} h(x^{*}) = f(x^{*})$$
위의 두 식을 1번에 넣고 부등호를 유지하면 다음과 같다.
$$L(x^{*},\alpha^{*},\beta^{*}) \le f(x^{*})+\alpha^{*} g(x^{*}) + \beta^{*} h(x^{*}) \le f(x^{*})$$
$$\therefore f(x^{*}) \le f(x^{*}) +\alpha^{*} g(x^{*}) + \beta^{*} h(x^{*}) \le f(x^{*})$$
최종적인 식을 얻기 위해서는 부등호 사이에 있는 \(\alpha^{*} g(x^{*}) + \beta^{*} h(x^{*})\)값이 0이 되어야 하나, Primal Condition에서 \(h(x^{*})=0\)이라 가정하였기 때문에 \(\alpha^{*} g(x^{*})\)을 만족하면 된다.
즉, 위에서 새롭게 추가된 New Condition을 만족하게 되면 Primal -> Duality + Strong Duality가 만족하게 된다.
사진 참조: ratsgo 블로그
Dual Representation of SVM
위의 Duality + KKT Condition을 SVM에 적용하면 다음과 같다.
$$min_{w,b}||w||$$
$$s.t(wx_j+b)y_j \ge 1$$
$$L(w,b,\alpha) = \frac{1}{2}ww-\sum_{j}\alpha_j[(wx_j+b)y_j-1]$$
위의 식에서 KKT Condition의 조건을 차례대로 적용하면 다음과 같다.
1. \(\partial L(x^{*},\alpha^{*},\beta^{*}) = 0\): Lagrange Multiplier Condition
- \(\frac{\partial L(w,b,\alpha)}{\partial w} \rightarrow w = \sum_{i=1}^{n} \alpha_i y_i x_i\)
- \(\frac{\partial L(w,b,\alpha)}{\partial b} \rightarrow 0 = \sum_{i=1}^{n} \alpha_i y_i\)
2. \(\alpha^{*} \ge 0\): Primal -> Duality Condition
$$\alpha_j \ge 0$$
3. \(\alpha^{*}g(x^{*}) = 0\): New Condition
$$\alpha_i ((wx_j+b)y_j-1)=0$$
참조
- 자세한 수식 유도: 문일철 머신러닝 강의
- Error를 허용하는 SVM Dual Representation: ratsgo 블로그
5.7 Kernel
Kernel이라는 것은 Mapping Function을 사용하여 Data의 차원을 늘려서 Linear하게 Classify를 못하는 문제를 Linear 하게 Classify하게 바꾼다는 의미이다.
XOR의 예시를 살펴보게 되면 다음과 같다.
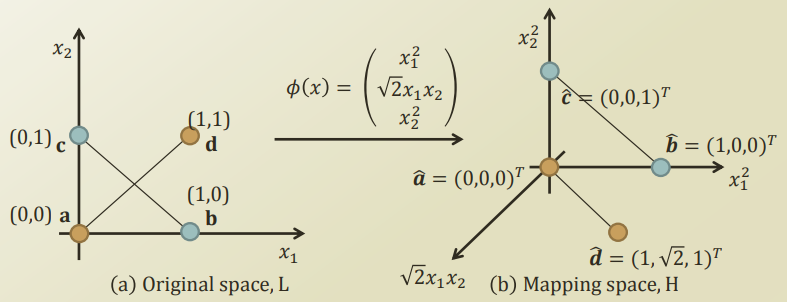
Linear로서 Classify하지 못했던 문제를 Mapping Function인 \(\pi(x)\)를 통하여 Data를 2->3차원으로서 변형시키고 Linear하게 Classify하게 한다.
이러한 간단한 Mapping Function을 사용하게 되면, Linear하게 계속하여 Space가 증가하게 된다. 따라서 이러한 Space를 작게 하고, 연산의 양을 줄이기 위하여 Kernel을 사용하게 된다.
먼저 Kernel의 식을 살펴보면 다음과 같다.
$$K(x_i,x_j) = \varphi(x_i) \cdot \varphi(x_j)$$
각각의 Data의 차원을 이동하는 \(\varphi\)의 내적으로서 표현한다는 것 이다.
이러한 Kernel의 대표적인 종류를 생각하면 다음과 같다.
- Polynomial: \(k(x_i,x_j) = (x_i \cdot x_j)^d\)
- Gaussian: \(k(x_i,x_j) = exp(-r||x_i - x_j||^2) (\text{단, }r = \frac{1}{2 \sigma^2})\)
- Hyperbolic tangent: \(k(x_i,x_j) = tanh(kx_i \cdot x_j+c) (\text{단, }k > 0, c<0 )\)
위에서 Polynormial일때를 생각하면 다음과 같이 나타낼 수 있다. Polynomial Function Degree 1
$$K(<x_1,x_2>,<z_1,z_2>) = <x_1,x_2> \cdot <z_1,z_2> = x_1z_1+x_2z_2 = x \cdot z$$
Polynomial Function Degree 2
$$K(<x_1,x_2>,<z_1,z_2>) = <x_1^2,\sqrt{2}x_1x_2,x_2^2> \cdot <z_1^2,\sqrt{2}z_1z_2,z_2^2> $$
$$= x_1^2z_1^2+2x_1x_2z_1z_2+x_2^2z_2^2 = (x \cdot z)^2$$
…
즉, Input으로 들어가는 Vector를 내적한다음 그 값을 곱하는 형식으로서 Data의 Dimension을 늘릴 수 있다.
이러한 특성으로서 Kernel Function은 1차원의 Data를 100차원으로 늘리는 경우 101번의 연산이 필요할 뿐이므로, 원하는 차원으로서 변형하는데 계산되는 양을 매우 줄이면서 Dimension을 늘릴 수 있다. => Dimension을 바꿈으로 인하여 Non-Linear하게 문제를 해결하는 것 처럼 만들 수 있다.
5.8 SVM with Kernel
위에서 최종적으로 얻은 식을 생각하면 다음과 같이 적용할 수 있다.
$$w = \sum_{i=1}^{N}\alpha_iy_ix_i$$
$$b = y_j - \sum_{i=1}^{N} \alpha_iy_ix_ix_j$$
$$\because y_j = w_jx_j+b_j$$
위의 식에서 Kernel을 적용하면 다음과 같이 나타낼 수 있다.
$$w = \sum_{i=1}^{N}\alpha_iy_i\varphi(x_i)$$
$$b = y_j - \sum_{i=1}^{N} \alpha_iy_i\varphi(x_i)\varphi(x_j) = y_j - \sum_{i=1}^{N} \alpha_iy_iK(x_i,x_j)$$
위의 w는 Kernel Trick 형식이 아닌 Mapping Function이다. 하지만 우리는 결국에 SVM의 식을 생각해보자. 즉, SVM은 궁극적으로 Input에 대하여 양수인지 음수인지로 Classification하는 Model이다.
식으로서 생각하면 다음과 같다.
$$sign(w \cdot x +b)$$
위의 식에 정리한 식을 대립하면 다음과 같은 결과를 얻게 된다.
$$sign(w \cdot \varphi(x) +b) = sign(\sum_{i=1}^{N}\alpha_iy_i\varphi(x_i)\cdot \varphi(x) + y_j - \sum_{i=1}^{N} \alpha_iy_iK(x_i,x_j))$$
$$= sign(\sum_{i=1}^{N}\alpha_iy_i K(x_i,x) + y_j - \sum_{i=1}^{N} \alpha_iy_iK(x_i,x_j))$$
즉, 실제 Model의 결과에서는 Kernel형태로 들어가게 되므로 문제없이 사용할 수 있다.
결과적으로 SVM은 Kernel Trick을 활용하여 Linear에서 해결하지 못하였던 문제를 NonLinear하게 해결할 수 있는 Classification Model로서 바뀌게 된다.


Leave a comment