Theory6. Training Testing and Regularization

6. Training Testing and Regularization

\(\newcommand{\argmin}{\mathop{\mathrm{argmin}}\limits}\) \(\newcommand{\argmax}{\mathop{\mathrm{argmax}}\limits}\) Machine Learning의 기초적인 이론부분을 다시 제대로 잡고 싶어서 문일철 교수님의 인공지능 및 기계학습 개론을 정리한 Post입니다.

• 6.1 Overfitting and Underfitting
• 6.2 Bias and Variance
• 6.3 Cross Validation
• 6.4 Performance Metrics
• 6.5 Defination of Regularization
• 6.6 Regularization with prior Knwlege

6.1 Overfitting and Underfitting

Dataset

• Training Dataset
  • Parameter inference procedure
  • Prior Knowledge, past experience
  • There is no guarantee that this will work in the future => Not General
• Testing Dataset
  • Testing the learned ML algorithms/the inferred parameters
  • New dataset that is unrelated to the training process

=> 즉, ML Algorithm의 단점으로는 Training된 Data의 Distribution에서만, 잘 작동 된다는 것 이다. 따라서 Dataset 중 일부를 Test Dataset으로서 Split하여 새로운 Data Distribution에 대한 Model의 성능을 측정해야 한다는 것 이다.

Overfitting and Underfitting Example

• Overfitting: 너무 Trainning Dataset에 Model이 Fitting되어진 상태(학습 오차는 작은데 테스트 오차가 큰 경우) => Test Dataset에서는 Model의 성능이 좋지 않을 것 이다.
• Underfitting: Trainning Dataset에도 Model이 Fitting되어진 못한 상태(학습 오차가 큰 경우) => Training Dataset, Test Dataset에서 모두 Model의 성능이 좋지 못한 상태이다.

Underfitting -> Overfitting으로 갈 수록 Complexity가 높아지는 것을 확인할 수 있다. Trade-off 관계이다.

6.2 Bias and Variance

ML에서의 Error는 다음과 같이 정의할 수 있다.

$$E_{out} \le E_{in}+\Omega$$

Machine Learning이라는 것은 실제 Target Function에 가까워지게 Modeling한 Function을 Approximation하는 과정이다. 이러한 과정에서 실제 Target Function과 Approximation Functio의 차이에서 생기는 Error가 바로 \(E_{in}\)이다.
또한 실제 Observation, Dataset의 Variance로 생기게 되는 Eorror가 바로 \(\Omega\)이다.

실제 이러한 Error에 관해서 수식으로 살펴보기 위하여 다음과 같이 Notation을 정하고 넘어가자.

• \(f\): Target function
• \(g\): Learning function of ML
• \(g^{(D)}\): The learned function by using a dataset D, or an instance of hypothesis
• \(D\): An available dataset drawn from the real world
• \(\bar{g}\): The average hypothesis of a given infinite number of D (\(\bar{g}(x) = E_{D}[g^{(D)}(x)]\))

즉, 우리는 \(g\)라는 Model을 설계하고 실제 우리가 얻을 수 있는 Dataset인 D를 Input으로 넣어서 Learning하여 \(g^{(D)}\)를 실제 Target Function인 f에 Approximation하는 과정이라고 할 수 있다.

위에서 정의한 Notation을 실제 정의한 Error를 정의하면 다음과 같이 정의할 수 있다.

$$E_{out}(g^{(D)}(x)) = E_{x}[(g^{(D)}(x)-f(x))^2]$$

즉, Estimation Error는 MSE를 사용하였을 경우 Model과 Target Function의 차이라고 생각할 수 있다.

위와 같은 과정에서 실제 Dataset을 Infinite Number라고 가정하자. 즉, 가능한 모든 Dataset을 D라고 하여야 보자. 그렇다면 수식을 다음과 같이 변경할 수 있다.

$$E_{D}[E_{out}(g^{(D)}(x))] = E_{D}[E_{x}[(g^{(D)}(x)-f(x))^2]] = E_{X}[E_{D}[(g^{(D)}(x)-f(x))^2]]$$

MSE이므로 Expectation이 Switch가 가능하며, 따라서 \(E_{D}[(g^{(D)}(x)-f(x))^2]\)을 좀 더 편하게 풀어보자.

$$E_{D}[(g^{(D)}(x)-f(x))^2] = E_{D}[(g^{(D)}(x) - \bar{g}(x)+\bar{g}(x)-f(x))^2]$$

$$= E_{D}[(g^{(D)}(x) - \bar{g}(x))^2]+(\bar{g}(x)-f(x))^2 + E_{D}[2(g^{(D)}(x) - \bar{g}(x))(\bar{g}(x)-f(x))]$$

$$\bar{g}(x) = E_{D}[g^{(D)}(x)] \rightarrow E_{D}[2(g^{(D)}(x) - \bar{g}(x))(\bar{g}(x)-f(x))] = 0$$

$$\therefore E_{D}[(g^{(D)}(x)-f(x))^2] = E_{D}[(g^{(D)}(x) - \bar{g}(x))^2]+(\bar{g}(x)-f(x))^2$$

$$\therefore E_{D}[E_{out}(g^{(D)}(x))] = E_{X}[E_{D}[(g^{(D)}(x) - \bar{g}(x))^2]+(\bar{g}(x)-f(x))^2]$$

최종적인 식을 크게 2부분으로 나누면 다음과 같은 2가지의 식을 얻을 수 있다.

• Variance(x)\(E_{D}[(g^{(D)}(x) - \bar{g}(x))^2]\)
• \(\text{Bias}^2(X) = (\bar{g}(x)-f(x))\)

각각의 의미는 다음과 같다.
Variance(x)는 실제 우리가 Observation가능한 Dataset과 모든 Dataset의 차이로서 이루워지는 차이이다. 즉, 실제 Observation의 Variance로 생기게 되는 Error(\(\Omega\))이다.
\(\text{Bias}^2(X)\)은 모든 Dataset으로서 학습한 Model이여도 결국 Funciton Approximation이므로 실제 Target Function과의 차이로 인한 Error(\(E_{in}\))이다. => Model의 한계로 인하여 발생하는 Error이다.

즉 각각의 해결방안은 다음과 같다.

• Reducing the variance: Collecting more datas
• Reducing the bias: More complex model

결과적으로 우리는 \(\bar{g}(x)\)을 Complexity를 추가하게 되어 실제 Target Function(f(x))에 가까워지게 만들게 되면은 Variance의 차이는 점점 커지게 된다는 것 이다.

이러한 과정을 좀 더 직관적으로 살펴보면 다음과 같이 생각할 수 있다.

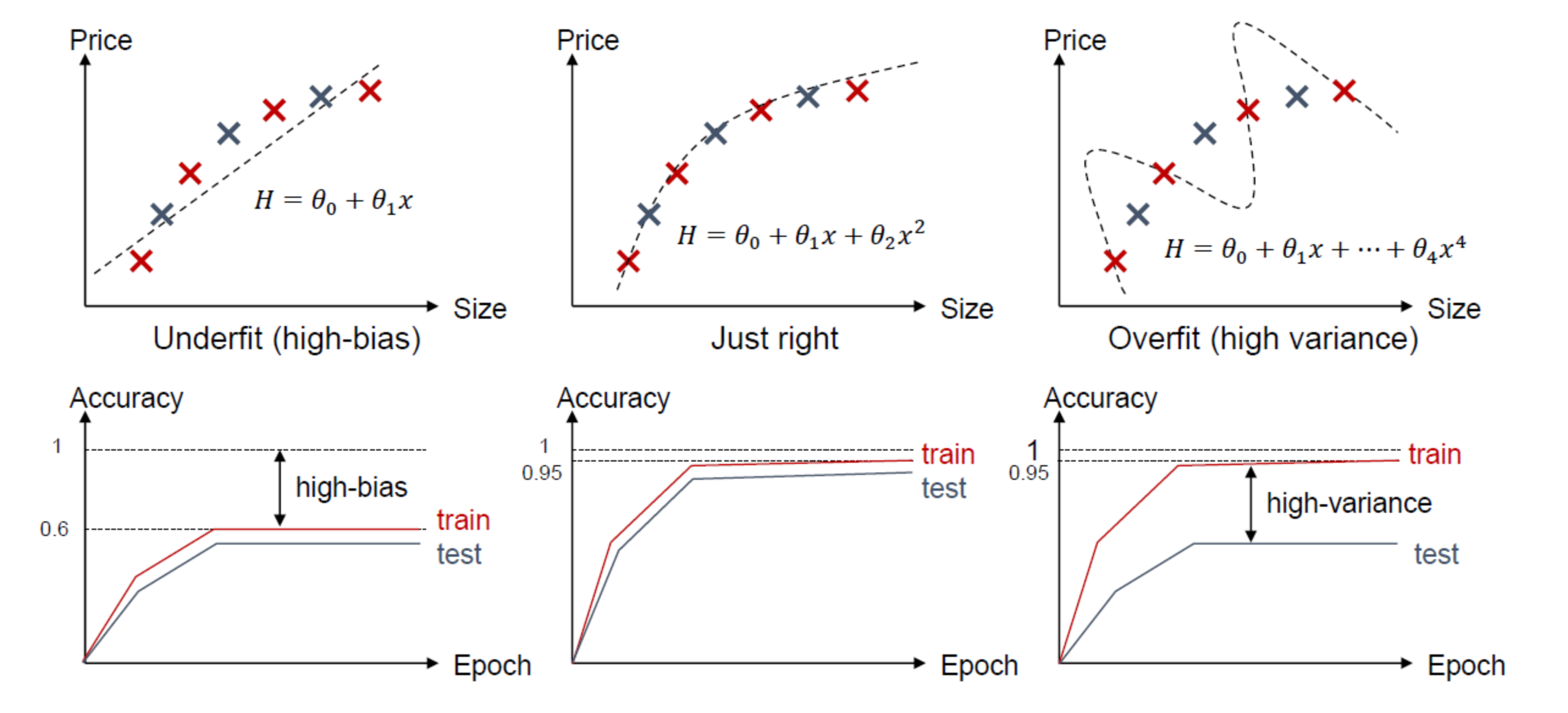
6.3 Cross Validation

Cross Validation 중 하나인 K-Fold Cross Validation을 알아보자.
K 개의 fold를 만들어서 진행하는 교차 검증
사용이유

• 총 데이터 갯수가 적은 데이터 셋에 대하여 정확도를 향상시킬 수 있음
• 기존에 Training, Validation, Test 세 개의 집단으로 분류하는 것보다, Trainning 과 Test로만 분류할 때 학습 데이터 셋이 더 많기 때문이다.
• 데이터 수가 적은데 검증과 테스트에 데이터를 더 뺏기면 underfitting 등 성능이 미달되는 모델이 학습됨

참조: ResearchGate

과정

• 기존 과정과 같이 Trainning Set과 Test Set을 나눈다.
• Trainning 을 K 개의 fold로 나눈다.
• 한 개의 Fold에 있는 데이터를 다시 K 개로 쪼갠다음, K-1개는 Trainning Data, 마지막 한개는 Validation Data Set으로 지정한다.
• 모델을 생성하고 예측을 진행하여, 이에 대한 에러값을 추출한다.
• 다음 Fold에서는 Validation 셋을 바꿔서 지정하고, 이전 Fold에서 Validation 역할을 했던 Set은 다시 Trainning set으로 활용한다.
• 이를 K번 반복한다.

6.4 Performance Metrics

먼저 자주사용하는 Accuracy로만 Model을 측정했을 경우 문제점을 생각해보면 다음과 같다.
Example) 희귀병을 진단하는 문제를 생각해보자. Dataset은 희귀병이므로 결국, Label이 1인 경우가 매우 적을 것이다. 다음과 같이 Label Dataset이 있다고 생각해 보자.

0,0,0,0, …, 1 의 Dataset이 있는경우 Model은 결국 어떤 Dataset이 들어오든지 간에 0으로서 판단하면 Accuracy가 90%이상이 나올 것 이다. 하지만, 관심있는 희귀병은 Classify하지 못 할 것이다. 따라서 Model을 Accuracy만으로서 판단하면 안되고 다른 Metrics또한 사용하여 Model의 성능을 측정해야 한다는 것 이다.

먼저 다음과 같은 Confusion Matrix가 있을 경우 각각의 Model의 성능을 측정하는 Metric은 다음과 같다.

	$\hat{y} = -1$	$\hat{y} = 1$
y = -1	TN	FP
y = 1	FN	TP

$$Accuracy = \frac{TP+FN}{TP+FP+FN+TN}$$

$$Precision = \frac{TP}{TP+FP}$$: Model이 참이라 하였을 때 실제 참일 확률

$$Recall = \frac{TP}{TP+FN}$$: 실제 참인데 Model이 참이라 분류할 확률

$$F_1 = \frac{2}{\frac{1}{Precision}+\frac{1}{Recall}} = \frac{TP}{TP+\frac{FN+FP}{2}} $$: 정밀도와 재형율의 조화평균(harmonic mean)

정밀도와 재현률에 대하여 예시를 살펴보면 다음과 같다.

1. 어린아이에게 안전한 동영상을 걸러내는 분류기를 훈련시킨다고 가정하면. 재현율은 높으나 정말 나쁜 동영상이 몇 개 노출되는 것보다 좋은 동영상이 많이 제외되더라도(낮은 재현율) 안전한 것들만 노출시키는(높은 정밀도) 분류기를 선호할 것 이다.
2. 감시 카메라를 통해 좀도둑을 잡아내는 분류기를 훈련시킨다고 가정하면, 분류기의 재현률이 99%라면 정확도가 30%만 되더라도 괜찮을 수 있다.(아마도 경비원이 잘못된 호출을 종종 받게 되겠지만, 거의 모든 좀도둑을 잡을 것입니다.)

이러한 정밀도와 재현률은 Tradeoff의 관계를 가지게 된다.
예를 들어 우리는 Precision을 늘리기 위한 방법으로는 FP를 줄이는 방법을 택해야 한다.
FP를 줄이기 위하여 Model에 특정 Threshold를 설정하여서 1로서 판단하는 기준을 조금 더 상승시킨다면, FP는 줄게 되겠지만, FN은 늘어나게 되어서 Recall은 감소하게 된다.
이러한 Threshold설정 방법이나 예시는 뒤에서 살펴볼 Perfomance measurement에서 실제 Code로서 살펴보자.

6.5 Defination of Regularization

Regularization이라는 기법은 결국 Model의 Variance를 줄인다는 의미이다. 즉, Model의 Complexity를 줄이기 위하여 Model의 Feature인 w를 0 or 0에 가까운 값으로서 수렴하게 한다는 것 이다. => 즉, Perpect Fitting은 포기하지만, Complexity는 줄여 Overfitting은 방지(avoid)한다는 의미이다.(Train Dataset에 대한 결과는 떨어진다.)

이러한 결과로서 Model에서의 Bias를 줄이기 위하여 Complex하게 유지하나 Variance를 줄이기 위하여 필요한 Weight만 가중치를 많이 주는 결과로서 Model이 Fitting되게 된다.(Training Dataset에 대한 Sensitivity를 줄인다.)

많이 사용되는 Regularization은 두가지이다.

위의 Regularization에서 L1 Regularization은 Lasso Regularization, L2 Regularization은 Ridge Regularizaiton이라고 불리기도 한다.

• L1 Regularization: \(E(w) = \frac{1}{2}\sum_{n=0}^{N}(train_n - g(x_n,w))^2 + \lambda||w||\)
• L2 Regularization: \(E(w) = \frac{1}{2}\sum_{n=0}^{N}(train_n - g(x_n,w))^2 + \frac{\lambda}{2}||w||^2\)

위에 두 Regularization을 살펴보게 되면, MSE + Regularization형태로서 Error를 측정하게 된다.
Regularization값이 커지면 커질 수록 즉, Weight의 값이 클 수록 Error가 증가하게 된다.
우리는 Error가 감소하는 방향으로 Training이 진행되므로, 특정 Weight가 커지는 것을 막는 효과가 있다고 생각할 수 있다.
결국 중요한 것은 \(\lambda\)를 설정해야 한다는 것 이다.

1. \(\lambda\)가 너무 크게 되면, Model의 Error측정은 무시 될 수 있고, 즉, Weight가 하나만 살아남게 될 것이다. 즉, Model의 Complexity가 전혀 없어지게 되고, Bias가 커지게 된다.
2. \(\lambda\)가 너무 작게 되면, Regularization은 무시 될 수 있고, 즉, Weight다 살아남게 된다. 즉, Model의 Complexity가 커지게 되고, Variance가 커지게 된다.

결과적으로 Regularization또한 \(\lambda\)에 따라서 Bias-Variance Trade off가 발생하게 되고, 여러번 반복해가면서 적절한 \(\lambda\)를 선택하는 Step이 필요하게 된다.

참고: L1 Regularization vs L2 Regularization
위의 결과를 살펴보게 되면 L1 Regularization은 특정 Weight가 0이 될 수 있지만, L2 Regularization을 사용하게 되면 0으로 죽는 것을 방지할 수 있다. 몇몇 Paper에서는 L1 Regularization을 사용하는 것이 더 효과가 있다고 설명하고 있습니다. 즉, 자신에 상황에 맞는 Regularization을 사용하는 것이 옳다고 할 수 있습니다.

6.6 Regularization with prior Knwlege

먼저 이전에 배웠던 MAP의 식을 사용하면 다음과 같이 나타낼 수 있다.

$$P(\theta|D) = \frac{P(D|\theta)P(\theta)}{P(D)}$$

$$Posterior = \frac{Likelihood*PriorKnowledge}{Normalizing Constant}$$

$$P(\theta|D) \varpropto P(D|\theta)P(\theta)$$

우리는 위의 식에서 w가 Gaussian Distribution 형태라는 Prior Knowledge를 정의하여 보자.

$$w \text{~} N(0,\sigma_w^2)$$

$$p(w) = \frac{1}{\sqrt{2\pi}\sigma_w}exp(-\frac{w^2}{2\sigma_w^2})$$

위와 같이 w에 대한 Prior Knowledge를 정의하고 MAP를 w를 통하여 Maximization한다면 다음과 같이 식을 정리할 수 있다.

$$w^{*} = \argmax_{w} P(w|D) = \argmax_{w} log(P(w|D))$$

$$\varpropto \argmax_{w} log(P(D|w))+log(P(w))$$

위의 식에서 \(\argmax_{w} log(P(D|w))\)는 Likelihood를 최대화 한다는 의미이다. 즉, 사용하고자하는 Model의 LossFunction을 L(w)라고 한다면, L(w)를 최소화 하는 문제라고 생각할 수도 있다. 따라서 LossFunction을 L(w)라고 한다면 \(\argmax_{w} log(P(D|w)) \rightarrow \argmax_{w} -L(w)\)로서 표현할 수 있다.

$$w^{*} = \argmax_{w} log(P(D|w))+log(P(w)) = \argmax_{w} -L(w)+log(P(\theta))$$

위의 식에서 우리는 P(w)에 대하여 Gaussian Distribution이라는 Prior Knowledge를 선언하였으므로 식을 다음과 같이 변형할 수 있다.

$$w^{*} = \argmax_{w} -L(w)+log(P(\theta))$$

$$= \argmax_{w} -L(w) -log(\sqrt{2\pi}\sigma_w)-\frac{w^2}{2\sigma_w^2}$$

위의 식을 Minimize형태로 다음과 같이 식을 변형시킬 수 있다.

$$w^{*} = \argmin_{w} L(w) + log(\sqrt{2\pi}\sigma_w) + \frac{w^2}{2\sigma_w^2}$$

위에서 선언한 L2 Regularization식을 살펴보면 다음과 같다.

$$E(w) = \frac{1}{2}\sum_{n=0}^{N}(train_n - g(x_n,w))^2 + \frac{\lambda}{2}||w||^2 = L(w) + \frac{\lambda}{2}||w||^2$$

즉, w가 Gaussian Distribution이라는 Prior Knowledge로서 주어지고 MAP를 적용한 식에서 \(log(\sqrt{2\pi}\sigma_w)\)을 Constant라고 제거한 식과 동일한 형태인 것을 알 수 있다.

최종적으로 우리는 L2 Regularization은 w가 Gaussian Distribution의 형태로서 Prior Knowledge를 적용한 것이며 L1 Regularization은 위와 같은 방식으로 w가 Laplacian Distribution이라는 Prior Knowledge를 적용한 MAP 형태라는 것을 추축할 수 있다.

Prior Knowledge가 w는 평균이 0인 Gaussian Distribution이므로 w값이 0에 가까운 값이 많이 분포하게 되어 Model의 Complexity를 줄이게 된다.

실질적인 예시를 알고 싶으면 링크를 참조하시길 바랍니다. hyeongminlee 블로그