Theory7. Bayesian Classifier
7. Bayesian Classifier
\(\newcommand{\argmin}{\mathop{\mathrm{argmin}}\limits}\) \(\newcommand{\argmax}{\mathop{\mathrm{argmax}}\limits}\) Machine Learning의 기초적인 이론부분을 다시 제대로 잡고 싶어서 문일철 교수님의 인공지능 및 기계학습 개론을 정리한 Post입니다.
- 7.1 Probability Concepts
- 7.2 Probability Theorems
- 7.3 Interpretation of Bayesian Network
- 7.4 Bayes Ball Algorithm
7.1 Probability Concepts, 7.2 Probability Theorems
기본적인 확률에 대한 이야기 이다.
기초적인 부분이며 다루는 범위가 많기 때문에 짧게 다루지 않고 Statistics에 하나의 Chapter로서 정리해 두었다.
앞으로 계속 사용하게 될 결과만 정리하면 다음과 같다.
Chain Rule or Factorization
$$P(a,b,c, ... z) = P(a|b,c,... z)P(b|c, ... z)P(c|...z)...P(z)$$
Joint Probability는 Conditional Probabilty로 인하여 Factorization형태로 나타낼 수 있다.
Independence
$$P(A|B) = P(A)$$
$$P(A,B) = P(A)P(B)$$
즉, B에 관계없이 Conditional Probability는 A와만 상관있다는 상황이다. => Independent하지 않으면 Joint Distribution에서 값을 구하기 복잡해진다.
- Marginal Independence: \(P(X,Y) = P(X)P(Y), P(X) = P(X|Y)\)
- Conditional Independence: $P(A|B,C) = P(A|C)$
$\rightarrow P(A,B|C) = P(A|B,C)P(B|C) = P(A|C)P(B|C)$ => C가 Given인 상황(Condition)에서는 B에 대해서 Independence하다.
Marginal Independence Conditional Independence는 앞으로 알아보게 될 Bayesian Network의 핵심이기 때문에 예시를 사용하여 알아보자.

참조: deadsquart 블로그
Commander : Y , OfficerA : X1, OfficerB : X2 라 가정.
OfficerA는 Commander 가 Go 라고 명령을 내렸는지 모른다고생각해보자. 그래서 OfficerA 가 Go 할지 말지 고민하고 있는데 , 옆의 OfficerB가 GO 하고 있어서 나도 GO를 했다고 해보자.
이렇게 되면 OfficerB의 행동(정보) 가 OffierA의 행동에 영향을 준것이다. 즉 두사람의 관계가 독립적이지 않다.
이번에는 OfficerA는 Commander 가 Go 라고 명령을 내린것을 들었다고 한다면 (조건) , 옆의 Officer B가 GO 하던 말던 옆사람의 정보(행동)에 관계없이 OfficerA 는 Go 하게 된다. 즉 Y(Latent variable)가 Given 이면(관측이 되었다면) X1, X2 사이에 Conditional independent 를 가정할수 있다.
Marginal independence 는 X1, X2 사이의 관계가 정의되지 않았다.
Conditional independence 는 Latent variable의 정보만이 X1의 행동에 영향을 준다. X1, X2 사이의 관계를 서로 독립이라 정의하였다.
7.3 Interpretation of Bayesian Network
이전 NaiveBayes Classifier에서 선언한 식을 다시 살펴보면 다음과 같다.
$$f^{*} = \argmax_{Y=y} P(Y=y|X=x) = \argmax_{Y=y}P(X=x|Y=y)P(Y=y)$$
$$\approx \argmax_{Y=y}\prod_{i=1}^n P(X_i=x_i|Y=y)P(Y=y)$$
즉, Y가 Given인 상황에서 X에 대한 확률을 최대화 하는 방법이다.
Bayesian Network는 이러한 관계를 Graphical Notation으로서 표현한 것이다. 즉, Node와 Link를 활용하여 NaiveBayes Classifier와 같은 Classifier를 Graphical하게 연결한 것 이다.
Syntax
- A acylick and directed graph: Graph는 Cycle한 구조가 되어서는 안되고 Direct가 있어야 된다.
- A set of nodes => Node는 Random variable이고, Node가 Link로 이어져 있으면 이어진 Parentes에 대한 Conditional Probability를 의미하게 된다.
- A random variable
- A conditional distribution given its partents = \(P(X_i|Parents(X_i))\)
- A set of links
- Direct influence from the parent to the child
위의 Syntax를 그림으로서 살펴보게 되면 다음과 같이 나타낼 수 있다.
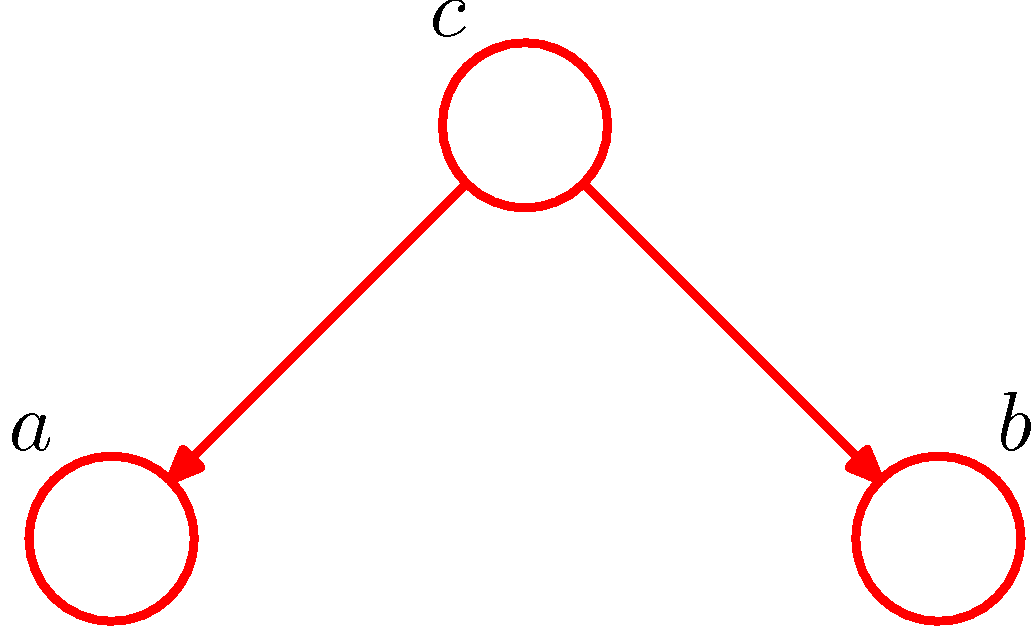
사진 출처: norman3 블로그
위의 그림을 살펴보게 되면 각각의 a,b,c는 Random Variable이며, a,b는 Parent c를 가지고 있다.
7.4 Bayes Ball Algorithm
참조: 이번 Part 경우는 norman3 블로그를 많이 참조하여 정리하였습니다.
Bayes Ball Algorithm이라는 것은 Bayesian Network의 Graph구조에서 Node끼리 Independent가 되기 위하여 관측되어야 할 Node를 정하는 Algorithm이다.
Conditional Independence의 조건을 다시한번 생각해보면 다음과 같다.
$$P(a,b,c) = p(a|b,c)p(b|c)p(c) (\because \text{Factorization}) \rightarrow^{if a \bot b | c} p(a|c)p(b|c)p(c)$$
Conditional Independence를 적용하여 Bayesian Network에서 대표적인 3가지 경우에 대해서 생각하면 다음과 같다.
Diverging Connections(Common parent)

사진 출처: norman3 블로그
위와 같은 상황일 경우 다음을 만족하지 않는다.
$$p(a,b,c) = p(a|b,c)p(b|c)p(c) \neq p(a|c)p(b|c)p(c) \rightarrow a \not\bot b | 0$$
위의 상황에서 만약, C가 Observation되었다고 하면 다음과 같이 변경 될 수 있다.(예시에서 Command가 명령을 내렸을 경우랑 같은 상황이다.)
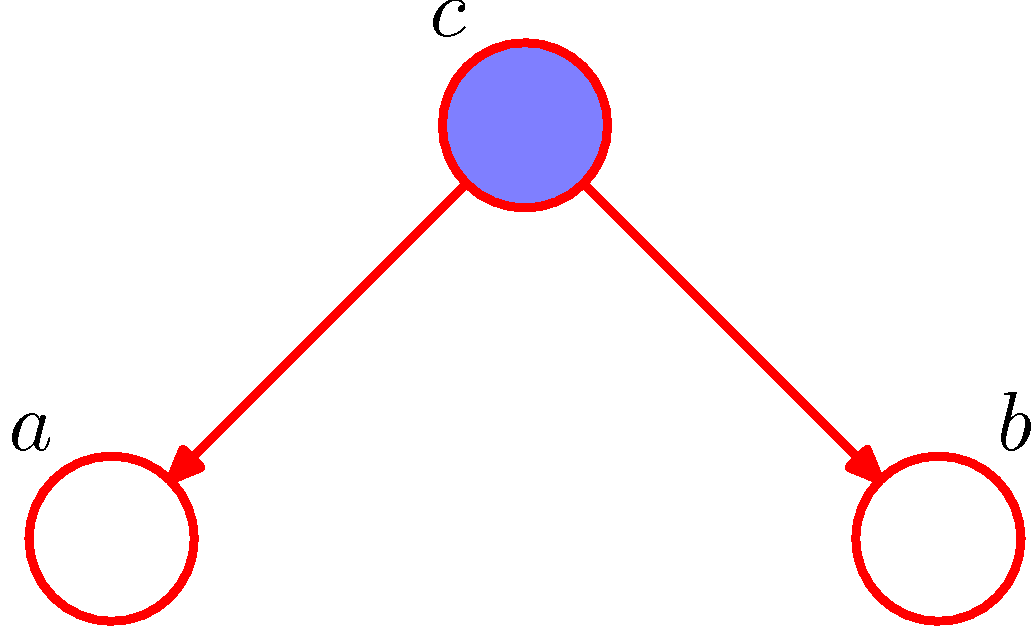
사진 출처: norman3 블로그
$$p(a,b|c) = \frac{p(a,b,c)}{p(c)} = p(a|c)p(b|c)$$
$$a\bot b | c$$
위와 같은 상황은 다음과 같이 정리할 수 있다.
- 노드가 두개의 화살표 꼬리 부분에 연결되어 있기 때문에 tail-to-tail 형태라고 한다.
- 노드 c를 관찰하게 되면 a와 b까지의 경로를 차단(block)하게 되어 a와b가 서로 조건부 독립이 된다.
Serial Connections(Cascading)
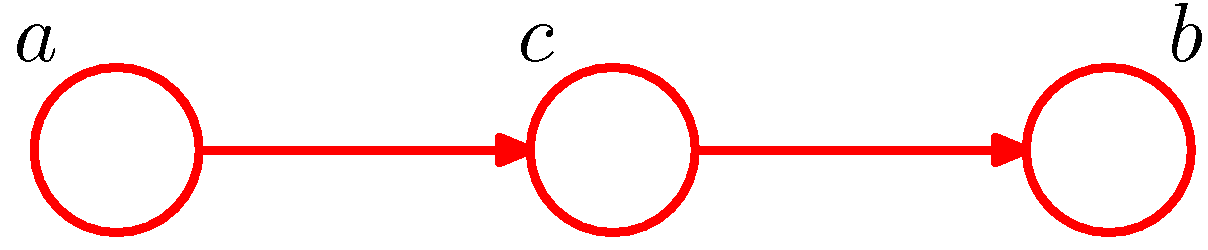
사진 출처: norman3 블로그
위와 같은 상황일 경우 다음을 만족하지 않는다.
$$p(a,b,c) = p(a|b,c)p(b|c)p(c) \neq p(a|c)p(b|c)p(c) \rightarrow a \not\bot b | 0$$
위의 상황에서 만약, C가 Observation되었다고 하면 다음과 같이 변경 될 수 있다.
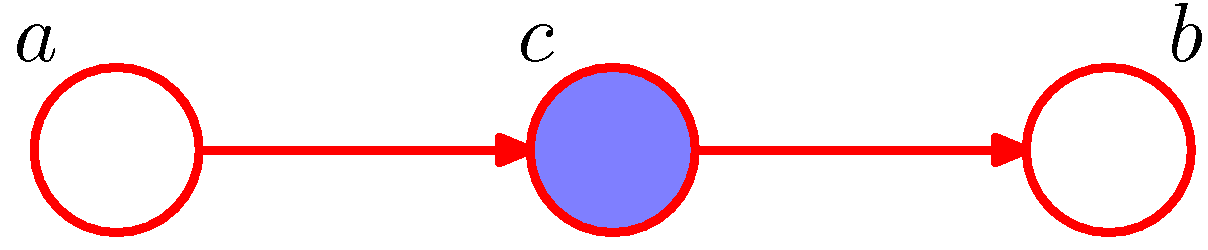
사진 출처: norman3 블로그
$$p(a,b|c) = \frac{p(a,b,c)}{p(c)} = p(a|c)p(b|c)$$
$$a\bot b | c$$
위와 같은 상황은 다음과 같이 정리할 수 있다.
- 하나의 화살표는 화살표의 머리가, 하나의 화살표는 화살표의 꼬리가 오기 때문에 head-to-tail 형태라고 한다.
- 노드 c를 관찰하게 되면 a와 b까지의 경로를 차단(block)하게 되어 a와b가 서로 조건부 독립이 된다.
Converging Connections(V-Structure)
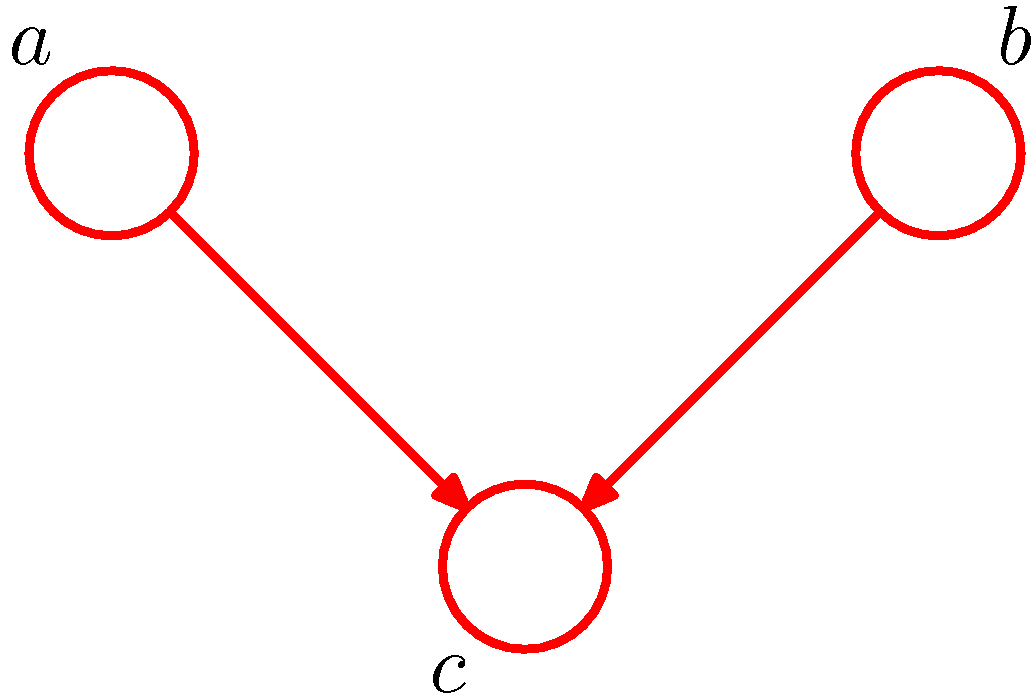
사진 출처: norman3 블로그
위와 같은 상황일 경우 다음을 만족하지 않는다.
$$p(a,b,c) = p(a|b,c)p(b|c)p(c) \neq p(a|c)p(b|c)p(c) \rightarrow a \not\bot b | 0$$
위의 상황에서 만약, C가 Observation되었다고 하면 다음과 같이 변경 될 수 있다.
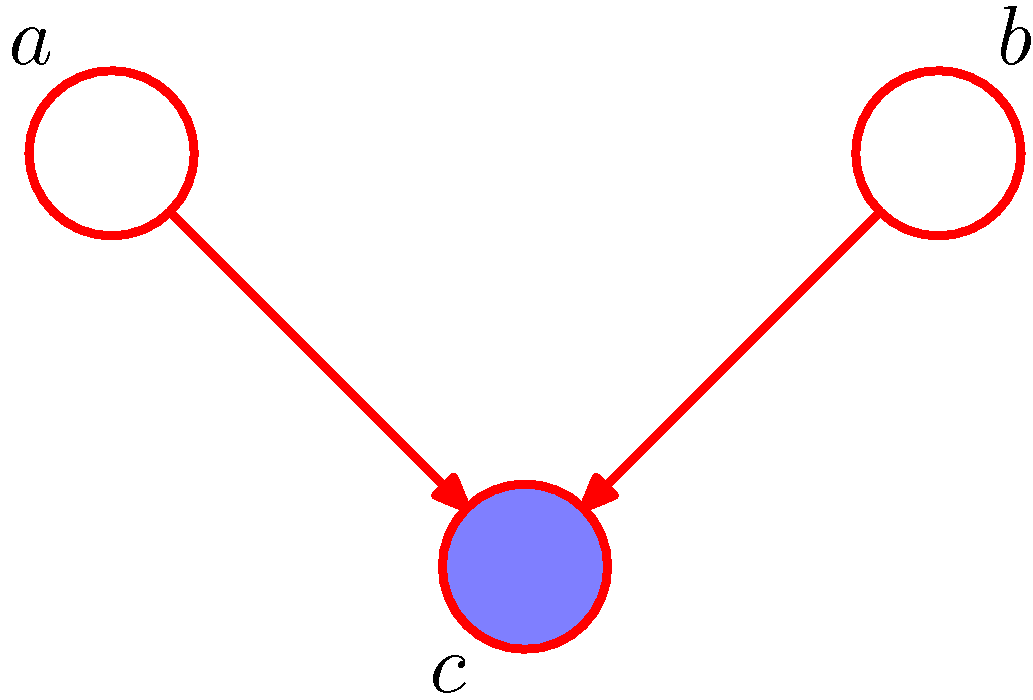
사진 출처: norman3 블로그
$$p(a,b|c) = \frac{p(a,b,c)}{p(c)} = p(a|c)p(b|c)$$
$$a\bot b | c$$
위와 같은 상황은 다음과 같이 정리할 수 있다.
- 노두가 두개의 화살표 머리 부분에 연결되어 있기 때문에 head-to-head 형태라고 한다.
- 노드 c를 관찰하게 되면 a와 b까지의 경로를 차단(block)하게 되어 a와b가 서로 조건부 독립이 된다.
즉, 서로 Conditional Independence하지 않은 2개의 Node에 대하여 특정 Node를 observation하게 되면 Conditional Independence한 형태로 변한다는 것 이다.
Markov Blanket
$$A \bot B | Blanket$$
$$Blanket = {parents, children, children's other parents}$$
위의 수식을 설명하게 되면, A라는 RandomVariable에 대하여 Blanket안의 값을 Observation하게 되면, Blanket바깥의 B Randomvariable에 대하여 Conditional Independent하다는 것 이다.
하나의 예제를 생각하면 다음과 같은 Bayesian Network와 A Random Variable을 생각하여 보자.

Markov Blanket에 의하여
- A Random Variable의 Parents => Cascading/Common parents의 경우 방지
- A Random Variable의 Children => Cascading의 경우 방지
- A Random Variable의 Childre’s other parents: V-Structure의 경우 방지
Markov Blanket의 결과는 다음과 같이 나타낼 수 있다.
 A와 노란원의 RandomVariable과의 관계는 Conditional Independence하다.
A와 노란원의 RandomVariable과의 관계는 Conditional Independence하다.

Leave a comment