Theory7. Bayesian Classifier(2)

7. Bayesian Classifier(2)

\(\newcommand{\argmin}{\mathop{\mathrm{argmin}}\limits}\) \(\newcommand{\argmax}{\mathop{\mathrm{argmax}}\limits}\) Machine Learning의 기초적인 이론부분을 다시 제대로 잡고 싶어서 문일철 교수님의 인공지능 및 기계학습 개론을 정리한 Post입니다.

• 7.5 Factorization of Bayesian networks
• 7.6 Inference Question on Bayesian Network
• 7.7 Variable Elimination
• 7.8 Potential Function and Clique Graph
• 7.9 Simple Example of Belief Propagation

7.5 Factorization of Bayesian networks

Bayesian Network의 확률은 Conditional Independence하다면 다음과 같이 나타낼 수 있다.

$$P(X) = \prod_{i}P(X_i|X_{\pi_i})$$

$$X_{\pi_i} = X_i \text{ 's Parent}$$

위와 같은 상황이면 Bayesian Network를 Factorization하였을 때 Parameter의 개수를 많이 줄일 수 있다는 것 이다.
예를 들어 다음과 같다.

$$P(x_1,x_2,x_3) = p(x_1 | x_2,x_3)p(x_2|x_3)p(x_3)$$

$$\rightarrow^{if x_1 \bot x_3 | x_2} p(x_1|x_2)p(x_2|x_3)p(x_3)$$

즉, \(p(x_1 | x_2,x_3)\)는 각각의 x가 true, false라면 4가지 상황에 대해서 생각해야 하지만, \(p(x_1 | x_2)\)이 되면 2가지 상황에 대해서만 생각하면 된다는 것 이다.

실제 Bayesian Network를 다음과 같이 주어졌을 경우 Joint Probability를 생각하여 보자.

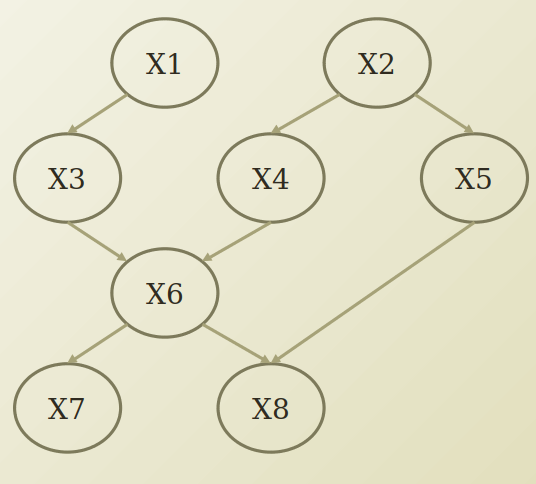
$$p(x_1,x_2,x_3,x_4,x_5,x_6,x_7,x_8,x_9)$$

$$=p(x_1)p(x_2)p(x_3|x_1)p(x_4|x_2)p(x_5|x_2)p(x_6|x_3,x_4)p(x_7|x_6)p(x_8|x_5,x_6)$$

7.6 Inference Question on Bayesian Network

Inference Question이라는 것은 Model이 Training이 된 후에, Model에 Query를 날려서 다른 예측값을 뽑아낼 수 있냐는 것 이다.
먼저, 사용하게 될 예제는 다음과 같다.

위의 그림을 살펴보게 되면, Bayesian Network로서 구성되어 있고, P(B), P(E), P(A|B,E), P(J|A), P(M|A)에 관한 확률을 모두 알 수 있다.(Model이 Training된 상황이기 때문이다.)

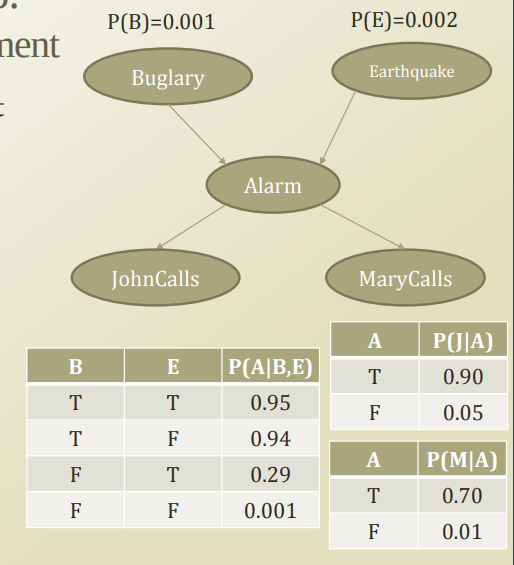
Notation
먼저, Inference Question모두에서 사용하는 Notation을 정하고 가면 다음과 같다.

• \(X=[X_1,X_2,...X_N]\): All random variable
• \(X_V=[X_{k+1}...X_N]\): Evidence random variable
• \(X_H=X-X_V=[X_1...X_k]\): Hidden random variable

위의 예제에 맞춰서 적용하면 각각은 다음과 같다.

• \(X=[B,E,A,J,M]\): All random variable
• \(X_V=[B,E]\): Evidence random variable
• \(X_H=X-X_V=[A,J,M]\): Hidden random variable

Inference Question1: Likelihood
Gin a set ofe, what is the likelihood of the evidence set?
\(X_V\)의 Likelihood를 구하여 보자.
General한 Formation으로 나타내면 다음과 같이 나타낼 수 있다.

$$P(X_V) = \sum_{X_H}P(X_H,X_V) = \sum_{X_1}...\sum_{X_k}P(X_1...X_k,X_V)$$

그렇다면 어떻게 계산을 할 수 있는가에 대해 살펴보게 되면, \(P(X_H,X_V)\)는 Full Joint 형식으로 변하게 된다.
따라서 위의 General Formation을 그림의 Problem에 적용하면 다음과 같이 식을 변형할 수 있다는 것 이다.

$$P(X_V) = \sum_{X_H}P(X_H,X_V)$$

$$ = \sum_{A}\sum_{J}\sum_{M}P(B)P(E)P(A|B,E)P(J|A)P(M|A)$$

위의 각각의 확률을 구해져 있으므로, 식을 계산할 수 있는 형태로서 변하게 된다.

Inference Question 2: Conditional Probability
Given a set of evidence, what is the conditional probability of interested hidden variables?
먼저 Hidden Variable을 다음과 같이 2개의 Variable로서 분류하여 보자.
\(X_H = [Y,Z]\)

• Y: Interested hidden variables
• Z: Un interested hidden variables

\(P(Y|X_V)\): Evidence가 주어진 경우, Interest한 Variable의 확률을 General한 Formation으로 나타내면 다음과 같다.

$$P(Y|X_V) = \sum_{z}P(Y,Z=z|X_V)$$

$$\sum_{z} \frac{P(Y,Z,X_V)}{P(X_V)} = \sum_{z} \frac{P(Y,Z,X_V)}{\sum_{y,z}P(Y=y,Z=z,x_v)}$$

위의 식을 자세히 살펴보게 되면 \(P(X_V)\)는 Inference Question1에서 구한 값이다. 즉, Full Joint에서 Uninterested Hidden Variable에 대하여 Marginalization하면 Interested한 Variable의 확률을 구할 수 있다는 것 이다.
따라서 위의 General Formation을 그림의 Problem에 적용하면 다음과 같이 식을 변형할 수 있다. (Y=J)로서 지정한다.

$$P(Y|X_V)$$

$$ = \frac{\sum_{A}\sum_{M}P(B)P(E)P(A|B,E)P(J|A)P(M|A)}{\sum_{A}\sum_{J}\sum_{M}P(B)P(E)P(A|B,E)P(J|A)P(M|A)}$$

Inference Question 3: Most Probable Assignment
위의 Bayesian Network의 결과값을 보면 다음과 같이 생각할 수 있다.

• B,E가 주어지면 A에 관하여 Prediction 가능하다. => B,E의 상태에 따라서 A의 확률을 결정할 수 있다.
• A가 주어지면 J,M의 상태에 대하여 Diagnosis가 가능하다. => A의 상태에 따라서 J,M의 상태를 확률로 결정할 수 있다.

7.7 Variable Elimination

Marginalization and Elimination
Marginalization을 통하여 확률의 곱셈에 대하여 Summation을 실시하게 된다. => 즉, Summation에 관계없는 확률은 Summation안에서 Elimination이 가능하다는 것 이다.
위의 Inference Question 1을 예시로 들면 다음과 같다.

$$P(X_V) = \sum_{X_H}P(X_H,X_V)$$

$$ = \sum_{A}\sum_{J}\sum_{M}P(B)P(E)P(A|B,E)P(J|A)P(M|A)$$

$$= P(B)P(E)\sum_{A}\sum_{J}\sum_{M}P(A|B,E)P(J|A)P(M|A)$$

위로서 변경하게 되어서 Computing을 많이 줄일 수 있다.

Variable Elimination
위의 Marginalization and Elimination을 좀더 Generalization한 형태로서 표현해보자.
구하고자 하는 확률은 \(P(E,J,M)\)이라고 하여보자. 이식을 Full Joint로서 표현하면 다음과 같이 나타낼 수 있다.

$$P(E,J,M) = \sum_{A}\sum_{B}P(B)P(E)P(A|B,E)P(J|A)P(M|A)$$

위의 식을 Marginalization and Elimination을 통하여 나타내면 다음과 같이 변형시킬 수 있다.

$$P(E,J,M) = P(E)\sum_{B}P(B)\sum_{A}P(A|B,E)P(J|A)P(M|A)$$

위의 수식에서 \(f_A(b) = P(B|A)\) 의 형태인 Function으로 정의하면 위의 식을 다음과 같이 정의할 수 있다.

$$P(E,J,M) = f_E(e)\sum_{B}f_{B}(b)\sum_{A}f_A(a,b,e)f_J(a)f_M(a)$$

위의 수식은 Inference Question on Bayesian Network에서 사용한 Example에 적용하면 다음과 같이 적용할 수 있다.

$$P(E,J,M) = f_E(e)\sum_{B}f_{B}(b)\sum_{A}f_A(a,b,e)f_{JM}(a)$$

$$P(E,J,M) = f_E(e)\sum_{B}f_{B}(b)\sum_{A}f_{AJM}(a,b,e)$$

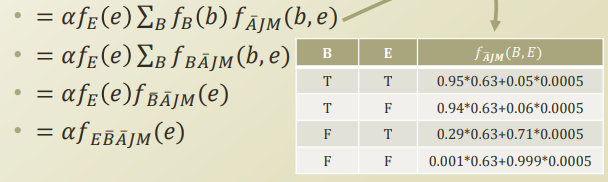
$$P(E,J,M) = f_E(e)\sum_{B}f_{B}(b)f_{\bar{A}JM}(a,b,e)$$

위와 같은 형식으로 계속하여 계산할 수 있다.

7.8 Potential Function and Clique Graph

Potential function: A function which is not a probability function yet, but once normalized it can be probability distribution function

• Potential function on nodes: \(\psi(a,b),\psi(b,c),\psi(c,d)\) => Clique
• Potential function on links: \(\phi(b), \phi(c)\) => Separateor

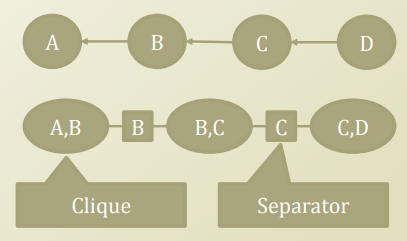
Potential Function이라는 것은 PDF로서 표현하기 위한 방법이다. Bayesian Network를 Clique(Fully Conntected)와 Separator로서 표현한다.

위의 그림을 Bayesian Network의 특성에 따라서 Full Joint로서 표현하면 다음과 같이 나타낼 수 있다.

$$P(A,B,C,D) = P(A|B)P(B|C)P(C|D)P(D)$$

위의 식을 각각의 Clique와 Separator로서 표현하면 다음과 같이 표현할 수 있다.

Notation 1(Conditional Probability)

$$P(A,B,C,D) = \frac{\prod_N \psi(N)}{\prod_L \phi(L)} = \frac{\psi(a,b)\psi(b,c)\psi(c,d)}{\phi(b)\phi(c)}$$

$$\because \psi(a,b) = P(A|B), \psi(b,c) = P(B|C)\psi(c,d) = P(C|D)P(D)$$

$$\because \phi(b)=1, \phi(c) =1$$

Notation 2(Joint Probability)

$$P(A,B,C,D) = \frac{\prod_N \psi(N)}{\prod_L \phi(L)} = \frac{\psi^{*}(a,b)\psi^{*}(b,c)\psi^{*}(c,d)}{\phi^{*}(b)\phi^{*}(c)}$$

$$\because \psi^{*}(a,b) = P(A,B), \psi^{*}(b,c) = P(B,C)\psi^{*}(c,d) = P(C,D)$$

$$\because \phi^{*}(b)=P(B), \phi^{*}(c) =P(C)$$

Bayesian Network의 Full Joint Factorization을 Clique, Separator로서 Clique-Conditional, Joint / Separator-1,Individual Probability 로서 나타낼 수 있다.

7.9 Simple Example of Belief Propagation

Belief Propagation이라는 것은 Bayesian Network 특성상 하나의 Random Variable이 Evidence Variable로 변함으로 인하여 연관있는 Probability가 변한다는 의미이다.

먼저 위의 상황에서 Joint Probability의 예시로 살펴보자.

Joint Probability

$$P(A,B) \rightarrow P(A=1,B): (\text{A: Observation -> Evidence})$$

$$\psi(A,B) \rightarrow \psi^{*}(A,B) (\because \psi(A,B) = P(A,B))$$

위와 같이 Notation을 정의하면 P(B)에 대하여 각각의 Margianlization을 다음과 같이 나타낼 수 있다.

$$P(B) = \sum_{A} \psi(A,B)$$

$$P(B) = \sum_{C} \psi(B,C)$$

$$P(B) = \phi(B)$$

$$\therefore P(B) = \sum_{A} \psi(A,B) = \sum_{C} \psi(B,C)= \phi(B)$$

위에서 \(P(A,B) \rightarrow P(A=1,B)\)로서 A가 Random -> Evidence Variable로 변형하였다. 이에 따라서 \(\sum_{A} \psi(A,B)\)값은 변하게 될 것이고, 등호 관계에 있는 모든 값들은 변하게 될 것 이다.

이러한 과정을 위의 그림에 대입하면 제일 앞의 Node가 변함에 의하여 모든 Node의 값이 변하게 되는 Belief Propagation이라고 불리게 된다.

$$\psi(A,B) \rightarrow \psi^{*}(A,B)$$

$$\phi^{*}(B) = \sum_{A} \psi^{*}(A,B)$$

$$\psi^{*}(B,C) = \psi(B,C)\frac{\phi^{*}(B)}{\phi(B)}$$

$$\because \sum_{C}\psi^{*}(B,C) = \sum_{C} \psi(B,C)\frac{\phi^{*}(B)}{\phi(B)}$$

$$= \frac{\phi^{*}(B)}{\phi(B)}\sum_{C} \psi(B,C) = \frac{\phi^{*}(B)}{\phi(B)}\phi(B) $$

Conditional Probability
실제 얻을 수 있는 Data는 Joint Probability가 아닌 Joint Probability이다.
따라서, Bayesian Network에 Conditional Probability를 활용하여 Belief Propagation을 실시하여 보자.
먼저, Bayesian Network를 다시 다음과 같다고 정의하여 보자.
위와 같은 Bayesian Network를 Clique Graph로서 변형하면 다음과 같이 나타낼 수 있다.

• \(\psi(a,b) = P(a|b), \psi(b,c) = P(b|c)P(c)\)
• $\phi(b) = 1$

위와 같은 경우에 다음과 같은 문제 2개를 생각해 보자.
Example 1. P(b)=?

$$\phi^{*}(b) = \sum_{a}\psi(a,b) = 1$$

$$(\because \sum_{a}\psi(a,b) = \frac{1}{P(b)}\sum_aP(a,b) = \frac{1}{P(b)}P(b))$$

$$\psi^{*}(b,c) = \psi(b,c)\frac{\phi^{*}(b)}{\phi(b)} = P(b|c)P(c) = P(b,c)$$

$$\phi^{**}(b) = \sum_{c}\psi(b,c) = \sum_{c} P(b,c) = P(b)$$

$$\psi^{*}(a,b) = \psi(a,b)\frac{\phi^{**}(b)}{\phi^{*}(b)} = P(a|b)P(b) = P(a,b)$$

$$\phi^{***}(b) = \sum_{a}\psi^{*}(a,b) = \sum_{a} P(a,b) = P(b)$$

위의 과정을 살펴보면 다음과 같은 결과를 얻을 수 있다.

• Conditional Probability -> Joint Probability
• \(\psi(a,b) = P(a|b) \rightarrow \psi^{*}(a,b) = P(a,b)\)
• 1 -> Indiviaul Probability
• \(\phi(b) \rightarrow \phi^{***}(b) = \phi^{**}(b) = P(b)\) => 값이 변하지 않는다. Local consitency를 Maintain하고 있다.

Example 2. P(b|a=1,c=1)=?
a,c가 Random Variable => Observation이 되었다고 생각하여 보자.

$$\phi^{*}(b) = \sum_{a}\psi(a,b)\delta(a=1) = P(a=1|b)$$

$$\psi^{*}(b,c) = \psi(b,c)\frac{\phi^{*}(b)}{\phi(b)} = P(b|c=1)P(c=1)P(a=1|b)$$

$$\phi^{**}(b) = \sum_{c}\psi(b,c)\delta(c=1) = P(b|c=1)P(c=1)P(a=1|b)$$

$$\psi^{*}(a,b) = \psi(a,b)\frac{\phi^{**}(b)}{\phi^{*}(b)}$$

$$=\frac{P(b|c=1)P(c=1)P(a=1|b)}{P(a=1|b)}P(a=1|b) = P(b|c=1)P(c=1)P(a=1|b)$$

$$\phi^{***}(b) = \sum_{a}\psi^{*}(a,b)\delta(a=1) = P(b|c=1)P(c=1)P(a=1|b)$$

$$P(b|c=1)P(c=1)P(a=1|b) = \frac{P(b,c=1)}{P(c=1)}P(c=1)\frac{P(b,a=1)}{P(b)}$$

$$= \frac{P(b,a=1)P(b,c=1)}{P(b)} = P(b|a=1,c=1)$$

위의 과정을 살펴보면 다음과 같은 결과를 얻을 수 있다.

• \(\psi()\)
• \(\psi(a,b) = P(a|b) \rightarrow \psi^{*}(a,b) = P(b|c=1)P(c=1)P(a=1|b)\)
• \(\psi(b,c) = P(b|c)P(c) \rightarrow \psi^{*}(b,c) = P(b|c=1)P(c=1)P(a=1|b)\)
• \(\phi()\)
• \(\phi(b) \rightarrow \phi^{***}(b) = \phi^{**}(b) = P(b|c=1)P(c=1)P(a=1|b)\) => 값이 변하지 않는다. Local consitency를 Maintain하고 있다.

즉, 위의 Clique Graph에서 (A,B)—(B)—(B,C)중 A,C과 관측되었으므로 => (A=Evidence , B)=(B#)—(B#)—(B#)=(B,C=Evidence), B는 양옆의 Evidence Variable에 의하여 Update되면서, (A,B) = (B) = (A,C)의 관계로 변하게 된다.

Example 3. P(b|a=1)=?
a,c가 Random Variable => Observation이 되었다고 생각하여 보자.

$$\phi^{*}(b) = \sum_{a}\psi(a,b)\delta(a=1) = P(a=1|b)$$

$$\psi^{*}(b,c) = \psi(b,c)\frac{\phi^{*}(b)}{\phi(b)} = P(b|c)P(c)P(a=1|b) = P(b,c)P(a=1|b)$$

$$\phi^{**}(b) = \sum_{c}\psi(b,c) = \sum_{c}P(b,c)P(a=1|b) = P(c)P(a=1|b)$$

$$\psi^{*}(a,b) = \psi(a,b)\frac{\phi^{**}(b)}{\phi^{*}(b)} =\frac{P(c)P(a=1|b)}{P(a=1|b)}P(a=1|b) = P(c)P(a=1|b)$$

$$\phi^{***}(b) = \sum_{a}\psi^{*}(a,b)\delta(a=1) = P(c)P(a=1|b)$$

위의 과정을 살펴보면 다음과 같은 결과를 얻을 수 있다.

• \(\psi()\)
• \(\psi(a,b) = P(a|b) \rightarrow \psi^{*}(a,b) = P(c)P(a=1|b)\)
• \(\psi(b,c) = P(b|c)P(c) \rightarrow \psi^{*}(b,c) = P(b,c)P(a=1|b)\)
• \(\phi()\)
• \(\phi(b) \rightarrow \phi^{***}(b) = \phi^{**}(b) = P(c)P(a=1|b)\) => 값이 변하지 않는다. Local consitency를 Maintain하고 있다.

즉, 위의 Clique Graph에서 (A,B)—(B)—(B,C)중 A가 관측되었으므로 => (A=Evidence , B)=(B#)—(B#)—(B#)!=(B,C), B는 A가 Evidence Variable에 의하여 Update되면서, (A,B) = (B) != (A,C)의 관계로 변하게 된다.

=> 아직 C는 Random Variable이므로 C에 따라서 (A,C)의 값은 등호로 변할 수 있다. (P(B,C)를 B에 대하여 Margianlization을 하여야 한다.)