OpenCV-임계값과 히스토그램 처리
참고사항
현재 Post에서 사용하는 Data를 만드는 법이나 사용한 Image는 github에 올려두었습니다.
임계값 영상
임계값
cv2.threshold(src, thresh, maxval, type): 고정된 임계값을 결정하고 결과를 보여주는 계산
parameter
- src: input(single-channel)
- thresh: 임계값
- maxval: 임계값을 넘었을 때 적용할 value
- type: thresholding type
thresholding type
cv2.THRESH_BINARY
$$ dst(x,y) = \begin{cases} maxval & \mbox{if } src(x,y) > thresh \\ 0 & \mbox{o.w} \end{cases} $$
cv2.THRESH_BINARY_INV
$$ dst(x,y) = \begin{cases} 0 & \mbox{o.w} \\ maxval & \mbox{if } src(x,y) > thresh \end{cases} $$
cv2.THRESH_TRUNC
$$ dst(x,y) = \begin{cases} thresh & \mbox{if } src(x,y) > thresh \\ src(x,y) & \mbox{o.w} \end{cases} $$
cv2.THRESH_TOZERO
$$ dst(x,y) = \begin{cases} src(x,y) & \mbox{if } src(x,y) > thresh \\ 0 & \mbox{o.w} \end{cases} $$
cv2.THRESH_TOZERO_INV
$$ dst(x,y) = \begin{cases} 0 & \mbox{if } src(x,y) > thresh \\ src(x,y) & \mbox{o.w} \end{cases} $$
참고사항
현재 실험결과 Color Image에도 각각의 Channel에 대한 Input값의 threshold가 적용된 것을 확인할 수 있다.
적응형 임계값
cv2.adaptiveThreshold(src, maxValue, adaptiveMethod, thresholdType, blockSize, C): 이미지의 작은 영역별로 thresholding하는 방법
parameter
- src: input(single-channel)
- thresh: 임계값
- maxval: 임계값을 넘었을 때 적용할 value
- adaptiveMethod: thresholding value를 결정하는 계산 방법
- blockSize: thresholding을 적용할 영역 사이즈
- C: 평균이나 가중 평균에서 차감할 값
adaptiveMethod
cv2.ADAPTIVE_THRESH_MEAN_C: 주변 영역의 평균값으로 결정
cv2.ADAPTIVE_THRESH_GAUSSIAN_C
참고사항(Gaussian Filter)
가우시안 필터란 정규분포 공식에서 평균값을 0으로 하여 유도한 분포이다.
- 순환 대칭으로서 smoothing하는 효과가 발생한다.
- 단일 돌출(Single peak)부분을 가진다. 즉 중앙에 위치한 pixel과 먼 pixel값들을 낮추는 효과로서 잡음제거 효과가 있다.
참조:opencv-python 홈페이지
참조:큼크 블로그
임계값 연산
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
src = cv2.imread('./data/heart10.jpg')
print(src.shape)
box_layout = Layout(display='flex',
flex_flow='row',
border='solid',
width='100%',)
wImg1 = widgets.Image(layout = widgets.Layout(border="solid"), width="25%")
wImg2 = widgets.Image(layout = widgets.Layout(border="solid"), width="25%")
wImg3 = widgets.Image(layout = widgets.Layout(border="solid"), width="25%")
items = [wImg1, wImg2, wImg3]
tmpStream = cv2.imencode(".jpeg", src)[1].tostring()
wImg1.value = tmpStream
# 120 넘는 값을 255로 변환, 나머지는 0
# 따라서 120값을 넘는 붉은 값, 검은 값들은 255가 되어서 더욱 붉어지고 나머지값은 없어진것을 확인 가능
ret,dst = cv2.threshold(src,120,255,cv2.THRESH_BINARY)
print('ret=',ret)
tmpStream = cv2.imencode(".jpeg", dst)[1].tostring()
wImg2.value = tmpStream
# THHRESH_OTSU를 적용하여 이미지를 이진화 하였다.
ret2,dst2 = cv2.threshold(src,200,255,cv2.THRESH_BINARY,cv2.THRESH_OTSU)
print('ret2=',ret2)
tmpStream = cv2.imencode(".jpeg", dst2)[1].tostring()
wImg3.value = tmpStream
box = Box(children=items)
display.display(box)
임계값 연산 결과
(1300, 866, 3)
ret= 120.0
ret2= 200.0

적응형 임계값 영상
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
src = cv2.imread('./data/Threshold.png',0)
src = cv2.medianBlur(src,5)
box_layout = Layout(display='flex',
flex_flow='row',
border='solid',
width='100%',)
wImg1 = widgets.Image(layout = widgets.Layout(border="solid"), width="25%")
wImg2 = widgets.Image(layout = widgets.Layout(border="solid"), width="25%")
wImg3 = widgets.Image(layout = widgets.Layout(border="solid"), width="25%")
wImg4 = widgets.Image(layout = widgets.Layout(border="solid"), width="25%")
items = [wImg1, wImg2, wImg3, wImg4]
tmpStream = cv2.imencode(".jpeg", src)[1].tostring()
wImg1.value = tmpStream
ret,dst = cv2.threshold(src,0,255,cv2.THRESH_OTSU+cv2.THRESH_BINARY)
tmpStream = cv2.imencode(".jpeg", dst)[1].tostring()
wImg2.value = tmpStream
dst2 = cv2.adaptiveThreshold(src,255,cv2.ADAPTIVE_THRESH_MEAN_C,cv2.THRESH_BINARY,51,7)
tmpStream = cv2.imencode(".jpeg", dst2)[1].tostring()
wImg3.value = tmpStream
dst3 = cv2.adaptiveThreshold(src,255,cv2.ADAPTIVE_THRESH_GAUSSIAN_C,cv2.THRESH_BINARY,51,7)
tmpStream = cv2.imencode(".jpeg", dst3)[1].tostring()
wImg4.value = tmpStream
box = Box(children=items)
display.display(box)
img.shape = (512, 512)
img.shape = (262144,)
img shape = (512, 512, 1)
적응형 임계값 영상 결과

히스토그램 계산
cv2.calcHist(images, channels, mask, histSize, ranges[, hist[, accumulate]])
parameter
- image: input
- channel: input image의 channel(특정 channel을 지정할 수 있다.)
- mask: 이미지의 분석 영역. None이면 전체 영역
- histSize: BINS 값
- ranges: Range값
히스토그램 계산
hist1 = cv2.calcHist(images=[src],channels=[0],mask=None, histSize=[4],ranges=[0,8])를 살펴보게 되면 결국 src의 0~8까지의 값(ranges)을 4등분한 범위안에 있는 숫자를 카운트하는 Code이다.
즉 결과를 해석하면 다음과 같다.
- 9: src의 원소중 0~1까지의 값이 9개
- 3: src의 원소중 2~3까지의 값이 3개
- 2: src의 원소중 4~5까지의 값이 2개
- 2: src의 원소중 6~7까지의 값이 2개
1
2
3
4
5
6
7
8
9
10
11
src = np.array([[0,0,0,0],
[1,1,3,5],
[6,1,1,3],
[4,3,1,7]
],dtype=np.uint8)
hist1 = cv2.calcHist(images=[src],channels=[0],mask=None, histSize=[4],ranges=[0,8])
print('hist1=',hist1)
hist2 = cv2.calcHist(images=[src],channels=[0],mask=None, histSize=[4],ranges=[0,4])
print('hist2=',hist2)
히스토그램 계산 결과
hist1= [[9.]
[3.]
[2.]
[2.]]
hist2= [[4.]
[5.]
[0.]
[3.]]
히스토그램 계산(그레이 스케일 영상)
같은 이미지일 경우 range의 범위는 같지만 histSize에 따라서 최종적인 histogram의 x축 범위를 지정할 수 있다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
src = cv2.imread('./data/lena.jpg',cv2.IMREAD_GRAYSCALE)
hist1 = cv2.calcHist(images=[src],channels=[0],mask=None, histSize=[32],ranges=[0,256])
hist2 = cv2.calcHist(images=[src],channels=[0],mask=None, histSize=[256],ranges=[0,256])
hist1 = hist1.flatten()
hist2 = hist2.flatten()
plt.figure(figsize=(20,4))
imgae1=plt.subplot(1,3,1)
imgae1.set_title('hist1:binX=np.arrange(32)')
plt.plot(hist1,color='r')
binX = np.arange(32)
plt.bar(binX,hist1,width=1,color='b')
imgae2=plt.subplot(1,3,2)
imgae2.set_title('hist1:binX=np.arrange(32)*8')
binX=np.arange(32)*8
plt.plot(binX,hist1,color='r')
plt.bar(binX,hist1,width=1,color='b')
imgae3=plt.subplot(1,3,3)
imgae3.set_title('hist2:binX=np.arrange(256)')
binX=np.arange(256)
#plt.plot(hist2,color='r')
plt.bar(binX,hist2,width=4,color='b')
plt.show()
히스토그램 계산(그레이 스케일 영상) 결과
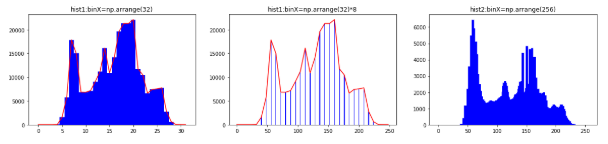
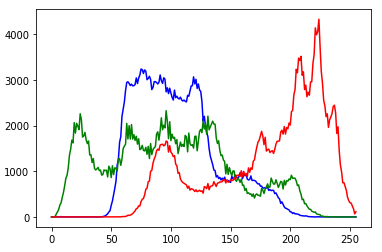
히스토그램 계산(컬러 영상)
Color Image를 Input으로 받아서 각각의 R, G, B값에 대한 히스토 그램 출력
1
2
3
4
5
6
src = cv2.imread('./data/lena.jpg')
histColor = ('b','g','r')
for i in range(3):
hist=cv2.calcHist(images=[src],channels=[i],mask=None, histSize=[256],ranges=[0,256])
plt.plot(hist,color=histColor[i])
plt.show()
히스토그램 계산(컬러 영상) 결과
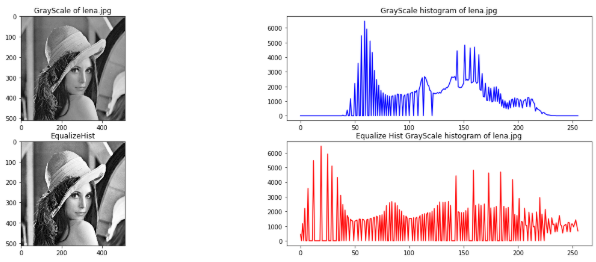
히스토그램 평활화
히스토그램 평활화 방법은 영상의 픽셀값들의 누적분포함수를 이용하여 영상을 개선하는 방법이다.
즉, 히스토그램 평활화는 화소값의 범위가 좁은 low contrast 입력 영상으로 화소값의 범위가 넓은 high contrast 출력 영상을 얻을 수 있다.
예를들어 특정 밝기 값에 몰려 어둡기만한 영상을 밝게 만들 수 있다.
히스토그램 평활화 과정
- src는 1채널 8비트(256) 입력 영상이다.
- src영상에서 히스토그램 H를 계산한다.
- 히스토그램 누적합계 \(H^{\prime}(i) = \sum_{0 \leq j \leq i}{H(j)}\)를 계산
- 히스토그램 누적합계(\(H^{\prime}(i)\))에 (255/\(H^{\prime}(255))\)를 곱한다.
- Roun Value
단, dst(x,y) = 0 if src(x,y) = 0
위의 과정을 아래 Code의 과정을 통하여 알아보자.
1
2
3
4
5
6
7
8
src = np.array([[0,0,0,0],
[1,1,3,5],
[6,1,1,3],
[4,3,1,7]
],dtype=np.uint8)
dst = cv2.equalizeHist(src)
print('dst=',dst)
히스토그램 평활화 결과
dst= [[ 0 0 0 0]
[106 106 170 212]
[234 106 106 170]
[191 170 106 255]]
위의 과정을 히스토그램 평활화 과정에 따라서 순차적으로 생각하면 다음과 같다.
| i | H(i) | $$H^{\prime}(i) = \sum_{0 \leq j \leq i}{H(j)}$$ | $$(255/H^{\prime}(255)) * H^{\prime}(i)$$ | Round Vlaue |
| 0 | 0 | 0 | 0 | 0 |
| 1 | 5 | 5 | 106.5 | 106 |
| 2 | 0 | 5 | 106.5 | 106 |
| 3 | 3 | 8 | 170 | 170 |
| 4 | 1 | 9 | 191.25 | 191 |
| 5 | 1 | 10 | 212.5 | 212 |
| 6 | 1 | 11 | 233.75 | 234 |
| 7 | 1 | 12 | 255 | 255 |
| ... | ... | ... | ... | ... |
| 255 | 0 | 12 | 255 | 255 |
위의 진행순서대로 하였을때 최종적인 결과가 같은 것을 알 수 있다.
그레이스케일 영상의 히스토그램 평활화
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
src = cv2.imread('./data/lena.jpg',cv2.IMREAD_GRAYSCALE)
dst = cv2.equalizeHist(src)
plt.figure(figsize=(20,7))
imgae1=plt.subplot(2,2,1)
imgae1.set_title('GrayScale of lena.jpg')
plt.imshow(src, cmap="gray")
imgae2=plt.subplot(2,2,3)
imgae2.set_title('EqualizeHist')
plt.imshow(dst, cmap="gray")
imgae3=plt.subplot(2,2,2)
imgae3.set_title('GrayScale histogram of lena.jpg')
hist1 = cv2.calcHist(images=[src],channels=[0],mask=None, histSize=[256],ranges=[0,256])
plt.plot(hist1,color='b')
imgae4=plt.subplot(2,2,4)
imgae4.set_title('Equalize Hist GrayScale histogram of lena.jpg')
hist2 = cv2.calcHist(images=[dst],channels=[0],mask=None, histSize=[256],ranges=[0,256])
plt.plot(hist2,color='r')
plt.show()
그레이스케일 영상의 히스토그램 평활화 결과
컬러영상의 히스토그램 평활화
- hsv에서 h(색조)를 Equalize함으로서 좀 더 진해진 진해진 느낌의 Image로 변환
- YCrCb에서 Y(밝기 성분)을 Equalize함으로서 좀 더 선명한 느낌의 Image로 변환
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
src = cv2.imread('./data/lena.jpg')
plt.figure(figsize=(20,7))
imgae1=plt.subplot(1,3,1)
imgae1.set_title('Original of lena.jpg')
src = cv2.cvtColor(src,cv2.COLOR_BGR2RGB)
plt.imshow(src)
#HSV
hsv = cv2.cvtColor(src,cv2.COLOR_BGR2HSV)
h,s,v = cv2.split(hsv)
v2 = cv2.equalizeHist(v)
hsv2 = cv2.merge([h,s,v2])
dst=cv2.cvtColor(hsv2,cv2.COLOR_HSV2BGR)
imgae2=plt.subplot(1,3,2)
imgae2.set_title('h of hsv equalizeHist')
plt.imshow(dst)
#YCrCb
YCrCb = cv2.cvtColor(src,cv2.COLOR_BGR2YCrCb)
Y,Cr,Cb = cv2.split(YCrCb)
Y2 = cv2.equalizeHist(Y)
YCrCb2 = cv2.merge([Y2,Cr,Cb])
dst=cv2.cvtColor(YCrCb2,cv2.COLOR_YCrCb2BGR)
imgae2=plt.subplot(1,3,3)
imgae2.set_title('Y of YCrCb equalizeHist')
plt.imshow(dst)
plt.show()
컬러영상의 히스토그램 평활화 결과

히스토그램 역투영
cv2.calcBackProject(const Mat* images, int nimages,
const int* channels, const SparseMat& hist,
OutputArray backProject, const float** ranges, double scale=1, bool uniform=true)
parameter
- images: input
- nimages: 입력 영상 개수
- channels: 역투영 계산 시 사용할 채널 번호 배열
- hist: 입력 히스토그램
- backProject: 출력 히스토그램 역투영 영상, 입력 영상과 같은 크기, 같은 깊이를 갖는 1채널 행렬
- ranges: 각 차원의 히스토그램 빈 범위
- scale: 히스토그램 역투영 값에 추가적으로 곱할 값
- uniform: 히스토그램 빈의 간격이 균등한지를 나타내는 플래그
히스토그램의 역투영이란?
히스토그램 역투영은 물체의 모양은 무시하고 단순히 컬러 분포만으로 검출하는 방법으로, 히스토그램은 컬러 분포를 표현하는데 사용된다.
이러한 특성 때문에 주의해야하는 점은 히스토그램이 명암 채널만 이용하는 1차원이 아니라 최소 2차원 이상을 사용한다.
이러한 이유는 명암은 조명에 따라 쉽게 변하며 비슷한 명암을 갖는 다른 영역이 있을 수도 있기 때문이다.
이러한 히스토그램역투영의 장점으로서 이동이나 회전이 발생하더라도 히스토그램은 변하지 않기 때문에 성능이 유지된다. 또한 물체의 일부가 가려진 경우에도 잘 작동된다.
배열의 히스토그램 역투영
1
2
3
4
5
6
7
8
9
10
11
src = np.array([[0,0,0,0],
[1,1,3,5],
[6,1,1,3],
[4,3,1,7]
],dtype=np.uint8)
hist = cv2.calcHist(images=[src],channels=[0],mask=None, histSize=[4],ranges=[0,8])
print('hist=',hist)
backP = cv2.calcBackProject([src],[0],hist,[0,8],scale=1)
print('backP=',backP)
배열의 히스토그램 역투영 결과
hist= [[9.]
[3.]
[2.]
[2.]]
backP= [[9 9 9 9]
[9 9 3 2]
[2 9 9 3]
[2 3 9 2]]
Hue-채널의 히스토그램 역투영
참고사항 ipywidgets(ROI)
이전 Post OpenCV 기본연산에서는 마우스 Click Event를 사용하여 ROI영역 지정을 찾았다.
이러한 ROI영역은 cv2.polylines()를 통하여 다각형으로 그렸지만 좀 더 계산을 편하게 하기 위하여 OpenCV ROI영역 지정과 같이 사각형으로서 ROI를 선택하여 진행도록 ipywidgets를 수정하였다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
class bbox_select():
%matplotlib notebook
def __init__(self,im):
self.im = im
self.selected_points = []
self.fig,ax = plt.subplots()
self.img = ax.imshow(self.im.copy())
self.ka = self.fig.canvas.mpl_connect('button_press_event', self.onclick)
disconnect_button = widgets.Button(description="Disconnect mpl")
display.display(disconnect_button)
disconnect_button.on_click(self.disconnect_mpl)
def poly_img(self,img,pts):
pts = np.array(pts, np.int32)
pt1 = pts[0,0],pts[0,1]
pt2 = pts[1,0],pts[1,1]
cv2.rectangle(img,pt1,pt2,(np.random.randint(0,255),np.random.randint(0,255),np.random.randint(0,255)),7)
cv2.rectangle(img,pt1,pt2,(0,255,0),2)
return img
def onclick(self, event):
self.selected_points.append([event.xdata,event.ydata])
if len(self.selected_points) == 2:
self.fig
self.img.set_data(self.poly_img(self.im.copy(),self.selected_points))
elif len(self.selected_points) == 3:
self.selected_points=[]
self.selected_points.append([event.xdata,event.ydata])
def disconnect_mpl(self,_):
self.fig.canvas.mpl_disconnect(self.ka)
1
2
im = plt.imread('./data/lena.jpg')
bs = bbox_select(im)
1
bs.selected_points
[[266.1843267108167, 414.0018395879323],
[308.56843267108167, 475.2233259749816]]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
hsv = cv2.cvtColor(im,cv2.COLOR_BGR2HSV)
h,s,v = cv2.split(hsv)
roi = []
for item in bs.selected_points:
roi.append(int(item[0]))
roi.append(int(item[1]))
roi_h = h[roi[0]:roi[1],roi[2]:roi[3]]
hist = cv2.calcHist([roi_h],[0],None,[64],[0,256])
backP=cv2.calcBackProject([h.astype(np.float32)],[0],hist,[0,256],scale=1.0)
hist = cv2.sort(hist,cv2.SORT_EVERY_COLUMN+cv2.SORT_DESCENDING)
k=1
T=hist[k][0]-1
print('T=',T)
ret,dst = cv2.threshold(backP,T,255,cv2.THRESH_BINARY)
plt.imshow(dst)
plt.show()
Hue-채널의 히스토그램 역투영 결과
1. ROI설정
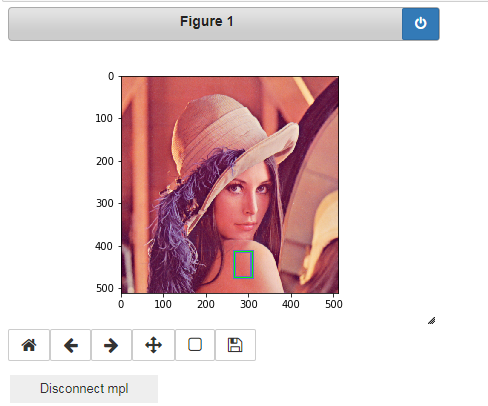
2. Hue-채널의 히스토그램 역투영
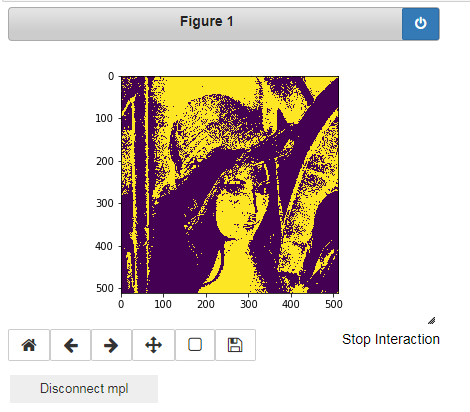
실행 결과 관심영역으로 지정한 ROI와 비슷한 색조의 pixel만 나타낸것을 알 수 있다
히스토그램 비교
CompareHist(hist1, hist2, method) : 두 히스토그램 분포를 비교하는 방법이다. 비교하는 방법은 method에 따라 달라진다.
parameters
- H1: First compared Histogram
- H2: Second compared histogram
- method: Comparison method
- cv2.HISTCMP_CORREL: Correlation
- cv2.COMP_CHISQR: Chi-Square
- cv2.COMP_INTERSECT: Intersection
- cv2.COMP_BHATTACHARYYA: bhattacharyya distance
정규분포 난수로 생성한 1차원 히스토그램 비교
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
%matplotlib notebook
nPoints = 100000
pts1 = np.zeros((nPoints,1),dtype=np.uint8)
pts2 = np.zeros((nPoints,1),dtype=np.uint8)
cv2.setRNGSeed(int(time.time()))
cv2.randn(pts1,mean=(128),stddev=(10))
cv2.randn(pts2,mean=(110),stddev=(20))
H1 = cv2.calcHist(images=[pts1],channels=[0],mask=None, histSize=[256],ranges=[0,256])
cv2.normalize(H1,H1,1,0,cv2.NORM_L1)
plt.plot(H1,color='r',label='H1')
H2 = cv2.calcHist(images=[pts2],channels=[0],mask=None,histSize=[256],ranges=[0,256])
cv2.normalize(H2,H2,1,0,cv2.NORM_L1)
plt.plot(H2,color='b',label='H2')
d1 = cv2.compareHist(H1,H2,cv2.HISTCMP_CORREL)
d2 = cv2.compareHist(H1,H2,cv2.HISTCMP_CHISQR)
d3 = cv2.compareHist(H1,H2,cv2.HISTCMP_INTERSECT)
d4 = cv2.compareHist(H1,H2,cv2.HISTCMP_BHATTACHARYYA)
print('df(H1,H2,CORREL)=',d1)
print('df(H1,H2,CHISQR)=',d2)
print('df(H1,H2,INTERSECT)=',d3)
print('df(H1,H2,BHATTACHARYYA)=',d4)
plt.legend(loc='best')
plt.show()
정규분포 난수로 생성한 1차원 히스토그램 비교 결과
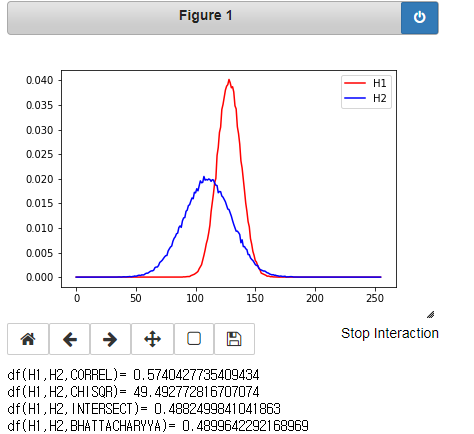
참조:원본코드
참조:Python으로 배우는 OpenCV 프로그래밍
문제가 있거나 궁금한 점이 있으면 wjddyd66@naver.com으로 Mail을 남겨주세요.


Leave a comment