Paper24. Deep learning enables accurate clustering with batch effect removal in single-cell RNA-seq analysis

Deep learning enables accurate clustering with batch effect removal in single-cell RNA-seq analysis

출처: Deep learning enables accurate clustering with batch effect removal in single-cell RNA-seq analysis
Blog: eleozzr GitHub Blog
코드: eleozzr GitHub

Abstract

Single-cell RNA sequencing (scRNA-seq) can characterize cell types and states through unsupervised clustering, but the ever increasing number of cells and batch effect impose computational challenges. We present DESC, an unsupervised deep embedding algorithm that clusters scRNA-seq data by iteratively optimizing a clustering objective function. Through iterative self-learning, DESC gradually removes batch effects, as long as technical differences across batches are smaller than true biological variations. As a soft clustering algorithm, cluster assignment probabilities from DESC are biologically interpretable and can reveal both discrete and pseudotemporal structure of cells. Comprehensive evaluations show that DESC offers a proper balance of clustering accuracy and stability, has a small footprint on memory, does not explicitly require batch information for batch effect removal, and can utilize GPU when available. As the scale of single-cell studies continues to grow, we believe DESC will offer a valuable tool for biomedical researchers to disentangle complex cellular heterogeneity.

Biomedical Data를 다루는데 있어서, 어려운 부분은 Sample의 수가 적다는 것 이다. 이러한 문제점을 해결하기 위하여, 단일 Dataset을 사용하지 않고, 여러 Dataset을 사용하는 경우가 많다. 하지만, 이러한 Data collection과정에서 서로 다른 Dataset간의 Batch-Effect가 발생한다.

이러한 Batch-Effect를 제거하는 것은 Classification performance를 높이는데 필수적이다. 해당 논문은 Unsupervised clustering method인 DESC로서, Batch-Effect를 제거할 수 있다. 특히, 해당 논문에서 주요한 점은 Batch-Effect가 어떠한 것이라고 Prior knowledge를 사용하지 않아도 되어, true biological variations보다 적은 Batch-Effect또한 제거 가능하다는 것 이다.

Introduction

Motivation
Batch effect is inevitable in studies involving human tissues because the data are often generated at different times and the batches can confound biological variations. Failure to remove batch effect will complicate downstream analysis and lead to a false interpretation of results.

Problem
(1) However, some studies might deplete or enrich certain cell types, which can lead to cell-type-specific batch effect. Even when processed together, some cell types might be more vulnerable to batch effect than others. Haghverdi et al. found that consideration of cell-type-specific batch effects rather than a globally constant batch effect for all cells leads to improved batch effect removal.
(2) For data with more than two batches, the first batch in order will be used as the reference batch to correct cells in the second batch, and the corrected values of the second batch are then added to the reference batch. (e.g., CCA, MNN, Seurat)

Solution
Since clustering and batch effect removal are interrelated, an ideal approach for batch effect removal should be performed jointly with clustering. It is also desirable to have a method that can simultaneously include cells from all batches in the analysis.

해당 논문의 Motivation은 downstream에서 정확히 분석하기 위하여 batch effect를 제거하는 것 이다.
이전의 Batch effect제거 방법은 2가지 문제가 발생하게 된다.

(1) 여러 Dataset을 사용하여 global하게 Batch-Effect를 제거하더라도, 일부 Dataset에서는 더 취약하여 제대로 Batch effect가 제거되지 않는다.

(2) 두 개 이상의 Batch effects를 제거하는 경우, 첫번째 Batch Effect를 기준으로 다음 Batch Effect를 선택하는 문제점 (e.g., CCA-Orthogoanl)

• (2-1) Batch Effect의 순서에 따라서 결과가 많이 달라지게 된다.
• (2-2) Correlation이 높은 Batch Effect 중 한개밖에 제거하지 못한다.

해당 논문은 clustering방법을 통하여 모든 Batch를 동시에 제거하는 방식인 DESC를 제안한다.

Method

Model Architecture

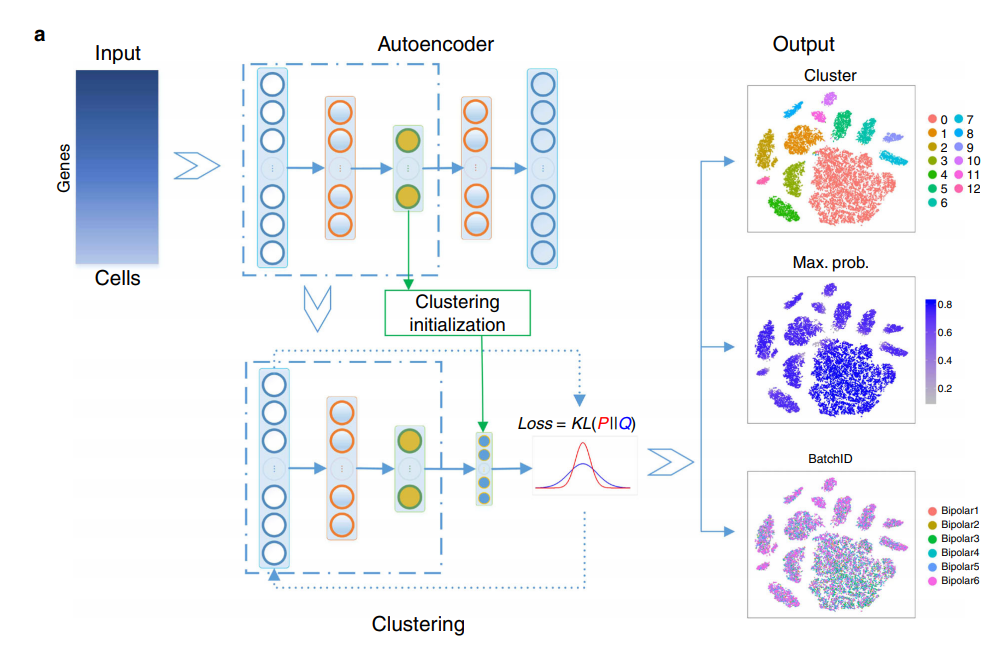
Define

• $X \in \mathbb{R}^{n \times p}$: Input Data
• $f_w(\cdot)$: Pretrained Encoder of Stacked AutoEncoder
• $z_i \in \mathbb{R}^{d} = f_w(x_i)$: Latent representation (d « p)
• $K$: Number of clusters
• ${u_j: j=1, \ldots, K}$: Cluster centroids

Parameeter initialization by stacked autoencoder
(1) Input Data는 sparsity하고 high dimensionality하기 때문에 Autoencoder를 통하여 low dimension인 latent representation에 mapping 한다.
(2) Stacked Autoencoder는 layer-wise training하여 점차적으로 training하게 된다.
(3) Pretrain된 Stacked Autoencoder의 Encoder부분을 Input으로서 사용한다.
(4) (3)의 Input을 사용하여 Louvain’s method를 사용하여 K개의 cluster개수와 해당되는 각각의 cluster centroids($u_j$)를 얻는다.

Iterative clustering
Stacked AutoEncoder를 Pretrain하고, Louvain’s method를 사용하여 cluster centroids($u_j$)를 학습한 뒤, AutoEncoder의 Encoder($f_w(\cdot)$)과 clutsering을 Iterative하게 학습하는 방법이다.

First Step.
먼저, kernel로서는 Student’s t distribution을 사용하여 embedding된 latenet representation($z_i$)를 clustering하였다.
아래 수식은 Latent Representation ($z_i$)가 cluster j 에 속할 확률이다.

$$q_{ij} = \frac{(1+ \| z_i - u_j\|^2 / \alpha)^{-1}}{\sum_{j^{'}} (1+ \| z_i - u_{j^{'}}\|^2 / \alpha)^{-1}}, \text{s.t. }\alpha: \text{Degree of freedom of Student's t distribution}$$

위와 같이 Student’s t distribution으로서 probability를 나타내어 Soft Clustering을 수행하였다.

Second Step.
KL divergence loss를 활용하여 Loss를 적용하면 다음과 같다.

$$L = KL (P || Q) = \sum_{i=1}^{n} \sum_{j=1}^{K} p_{ij} log \frac{p_{ij}}{q_{ij}},$$

$$p_{ij} \frac{q_{ij}^2 / \sum_{i=1}^n q_{ij}}{\sum_{j=1}^{K} (q_{ij}^2 / \sum_{i=1}^n q_{ij})}$$

기본적으로 많이 사용하는 Clustering에서의 KL-Divergence형태를 띄고 있다.
해당 논문에서 주요한 점은 이러한 Clustering을 통하여 생긴 Loss를 각각의 cluster center와 latent representation에 gradient를 전달할 수 있어 backpropagation이 가능하다는 것 이다.

$$\frac{\partial L}{\partial z_i} = \frac{\alpha +1}{\alpha} \sum_{j=1}^{K} *(1+ \frac{z_i - u_j^2}{\alpha})^{-1} x (p_{ij} - q_{ij})(z_i - u_j)$$

$$\frac{\partial L}{\partial u_i} = \frac{-(\alpha +1)}{\alpha} \sum_{i=1}^{n} *(1+ \frac{z_i - u_j^2}{\alpha})^{-1} x (p_{ij} - q_{ij})(z_i - u_j)$$

참조: Layer-wise training in stacked Autoencoder

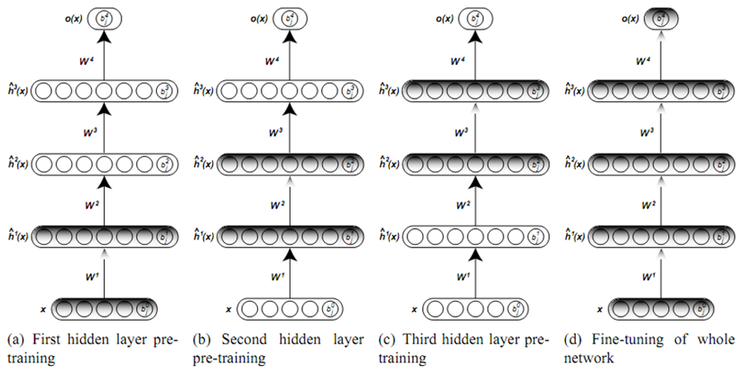
그림 참조: 라온피플 블로그
Layer-wise training은 Layer1를 학습한 뒤, weight를 고정하고, 다음 Layer를 학습하는 방법으로서 점차적으로 AutoEncoder를 학습하는 방법이다. 이러한 방식으로 학습하게 되면, 기존보다 Model의 Architecture를 깊게 쌓을 수 있다는 장점이 있다.

참조: Louvain’s method

• Modularity: Mons 1220 Blog
• Louvain’s method: Mons 1220 Blog

참조: Clustering Kernel = Gaussian Filter
Gaussian Filger를 사용하면 probability는 다음과 같이 나타낼 수 있다.

$$q_{ij} = \frac{\text{exp}(\frac{- \| z_i - u_j \|^2}{2 \alpha^2})}{\sum_{j^{'}} \text{exp}(\frac{- \| z_i - u_{j^{'}} \|^2}{2 \alpha^2})}$$

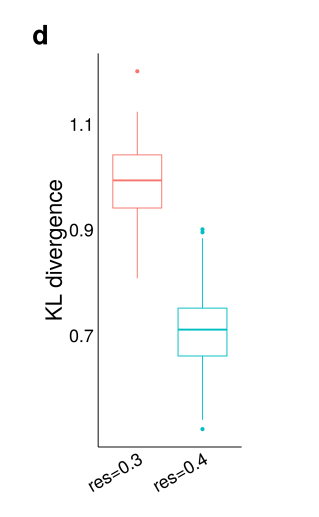
해당 논문의 저자들은 pancreatic islet data에 적용하였을 때, Gaussian Filter를 사용하게 되면, 아래의 그림과 같이 resolution에 따라 result의 차이가 큰, robust하지 않은 Model이 되어서 사용하지 않았다고 나와있다.

Result

Dataset: Retina data with complex batch effect.

• Label: Celltype
• Batch Effect1: macaquelD
• Batch Effect2: regionlD
• Batch Effect3: sampleID

Result: Visualization & Clasification with Batch Effect Information

• Metric: Clutering accuracy(ARI (adjusted Rand index))

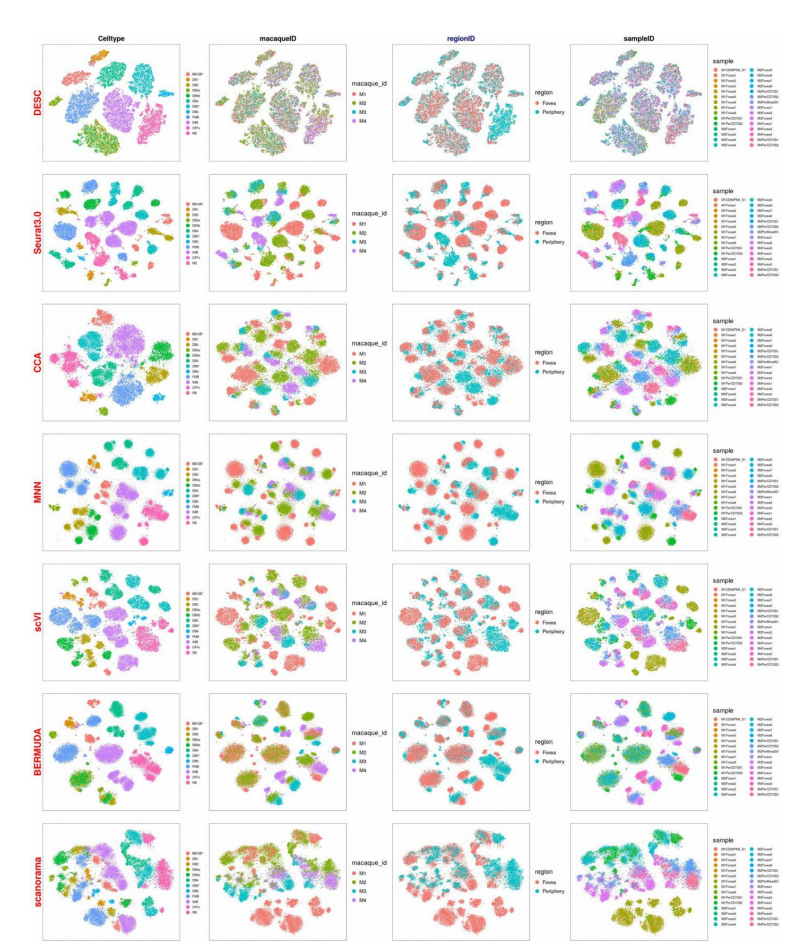
실제 Model training후에 Embedding을 Visualization하여 확인하게 되면, DESC는 Celltype에 대해서 자 구별함과 동시에 다른 Batch Effect도 제거된 것을 알 수 있다. Comparison Method들 중, scVI를 제외하고 모든 Methods는 prior knowlede로서 Batch Effect를 제거해야 한다.
제안하고자 하는 Model과 scVI를 사용하여, Batch Effect를 Prior knowledge로서 사용하지 않고, Batch Effect를 제거했을 때의 결과는 아래와 같다.

Result: Visualization & Clasification without Batch Effect Information

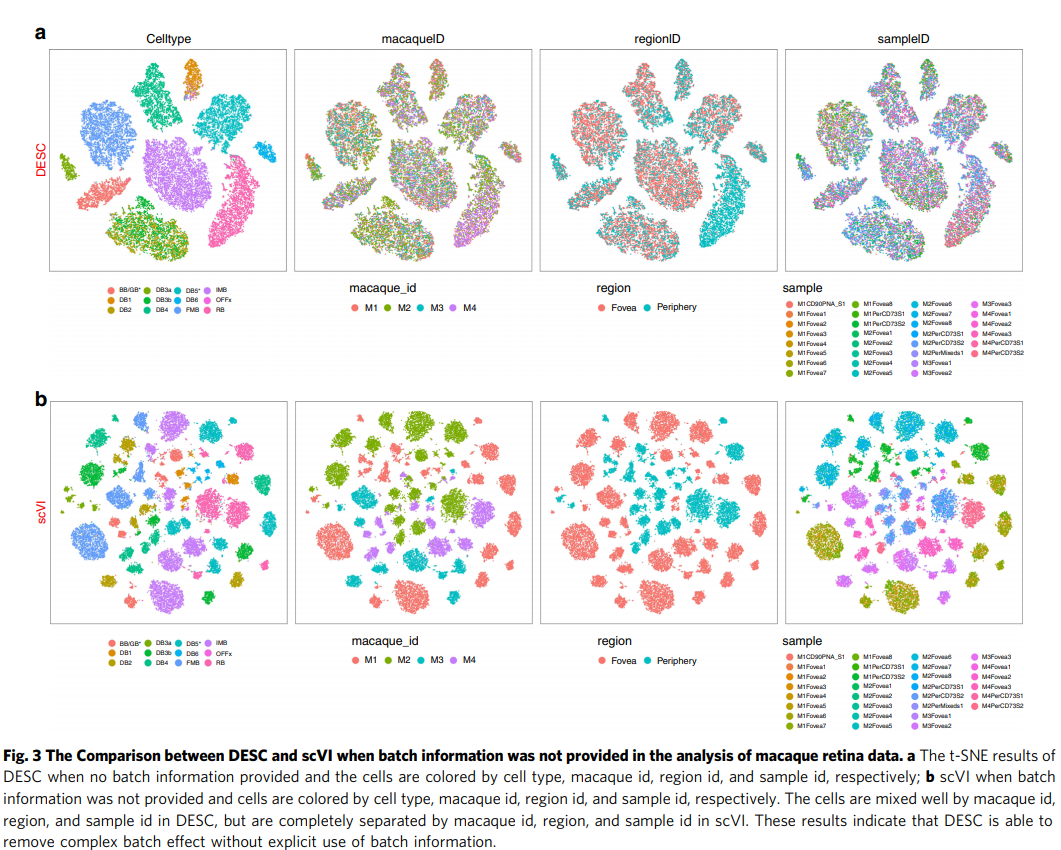
Discussion

개인적으로는 흥미롭게 봤던 논문인다. 특히, DNN의 Clustering을 연결하여 End-to-End로 지정한 논문은 개인적으로 처음이였다. 하지만, 해당 논문을 읽었을때, 많은 Dataset에 적용하여 Generalization을 보여주었지만, 왜 Batch-Effect가 사라지는지에 대해서는 수식을 보거나 Code를 살펴보았을때에도 이해할 수 없었다.