Paper29. Auto-Encoding Variational Bayes

Auto-Encoding Variational Bayes

이 Poster는 아래 논문과 Blog들을 참조하여 정리하였다는 것을 먼저 밝힙니다.

• Paper: https://arxiv.org/pdf/1312.6114.pdf
• 참조 Blog
  • (1). 초짜 대학원생의 입장에서 이해하는 Auto-Encoding Variational Bayes (VAE) (1),(2), (3)
  • (2). Gorio Learning Blog - VAE
  • (3). Ratsgo’s Blog - Variational Inference
  • (4). TENSORMSA Blog
  • (5). Andac Demir Blog

Abstract

How can we perform efficient inference and learning in directed probabilistic models, in the presence of continuous latent variables with intractable posterior distributions, and large datasets? We introduce a stochastic variational inference and learning algorithm that scales to large datasets and, under some mild differentiability conditions, even works in the intractable case. Our contributions is two-fold. First, we show that a reparameterization of the variational lower bound yields a lower bound estimator that can be straightforwardly optimized using standard stochastic gradient methods. Second, we show that for i.i.d. datasets with continuous latent variables per datapoint, posterior inference can be made especially efficient by fitting an approximate inference model (also called a recognition model) to the intractable posterior using the proposed lower bound estimator. Theoretical advantages are reflected in experimental results.

VAE (Variational AutoEncoder)의 목적은 random variable에서 원본 input을 어떻게 generation 할 것인지에 대한 model이며, 이에 대하여 생기는 문제에 대하여 approximation하여 해결할 수 있는 방안을 제시한다.

Notation

• \(X = \{x^{(i)}\}_{i=1}^N\): i.i.d. samples.
• \(z^{(i)}\): Unobserved continuous random variable.
• \(\theta\): Parameter of Generator (Decoder)
• \(\phi\): Parameter of Discriminator (Encoder)
• \(p_{\theta^*} (z)\): Prior distribution. \(z^{(i)}\) generated from \(p_{\theta^*} (z)\)
• \(p_{\theta^*} (x|z)\): Conditional distribution. \(x^{(i)}\) generated from \(p_{\theta^*} (x|z)\)
• \(q_{\phi} (z|x)\): Encoder
• \(p_{\theta} (x|z)\): Decoder

Problem

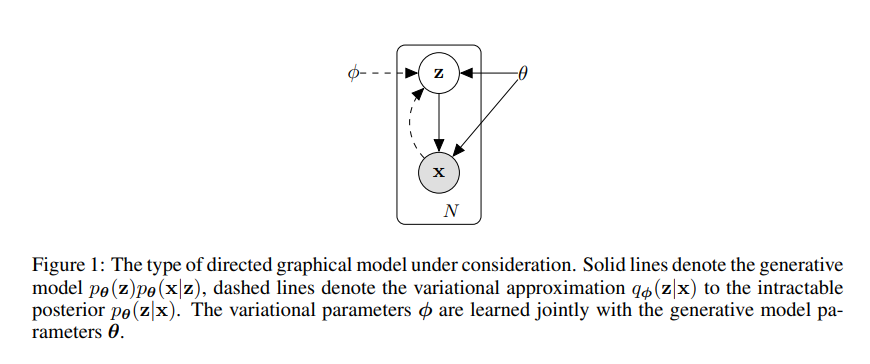
Generation Model인 VAE에서 해결하고자 하는 문제는 위의 Figure와 같다.
즉, Data (\(x\))는 어떠한 random variable에서 \(z\) 생성 (\(p_{\theta^*} (x|z)\))되었다고 가정하게 되면, \(z\)와 \(\theta\)를 알 수 있다면, sampling을 통하여 생성할 수 있다는 것 이다.

하지만, 위와 같은 문제를 해결하기 위해서는 해결해야하는 2가지 문제점이 있다.

1. Random variable (\(z\))는 측정할 수 없는 값 이라는 것 이다. 이러한 문제점을 해결하기 위하여 해당 논문에서는 Encoder를 활용하여 Data (\(x\))를 통하여\(z\)를 예측한다.
2. \(\theta\)를 모른다는 점이다. 이것은 Model구성 시에 충분히 Training을 통하여 학습될 수 있는 값 이다.

Variance Inference

VAE의 Loss Function을 이해하기 위하여 먼저 알고 있어야 되는 개념이 “Variance Inference (VI)”이다.
“VI란 사후확률(posterior)분포 \(p(z|x)\)를 다루기 쉬운 확률분포 \(q(z)\)로 approximation하는 것을 의미한다.”
사용하는 경우는 다음과 같이 3가지 경우가 있다.

• marginal probability, 즉 posterior의 분모인 \(p(x) = \sum_{z}p(x,z)\)를 계산하기 어려운 경우
• likelihood, 즉\(p(x|z)\)를 더 복잡하게 모델링 하고 싶은 경우
• prior, 즉 \(p(z)\)를 더 복잡하게 모델링 하고 싶은 경우

KL Divergence
어떠한 두 분포 사이에서 유사도를 계산하기 위한 방법으로서는 Kullback-Leibler divergence(KL-Divergence)을 사용하게 된다.
즉, \(p(z|x)\)와 \(q(z)\)와 사이의 KLD를 최소화할 수 있는 \(q^{*}(z)\)를 구한다.

$$D_{KL}(q(z) || p(z|x)) = \int q(z) \log \frac{q(z)}{p(z|x)} dz$$

$$= \int q(z) \log \frac{q(z) p(x)}{p(x|z) p(z)} dz$$

$$(\because p(x)p(z|x) = p(x|z)p(z))$$

$$= \int q(z) \log \frac{q(z)}{p(z)} dz + \int q(z) \log p(x) dz - \int q(z) \log p(x|z) dz$$

$$= D_{KL}(q(z) || p(z)) + \log p(x) - E_{z \text{~} q(z)}[ \log p(x|z) ]$$

Variational Inference with Monte Carlo sampling
몬테카를로 방법(Monte Carlo Method)이란 랜덤 표본을 뽑아 함수의 값을 확률적으로 계산하는 알고리즘이다.
예를들어 특정확률 분포를 따르는 x의함수값의 기대값은 다음과 같이 k개의 sample로서 근사하는 식은 아래와 같다.

$$\int { p\left( x \right) f\left( x \right) dx } ={ E }_{ x\sim p\left( x \right) }\left[ f(x) \right] \approx \frac { 1 }{ K } \sum _{ i=0 }^{ K }{ { \left[ f({ x }_{ i }) \right] }_{ { x }_{ i }\sim p\left( x \right) } }$$

위와 같은 Monte Carlo Method을 KLD에 적용하면 식을 다음과 같이 정리할 수 있다.

$$D_{KL}(q(z) || p(z|x)) = D_{KL}(q(z) || p(z)) + \log p(x) - E_{z \text{~} q(z)}[ \log p(x|z) ]$$

$$E_{z \sim q(z)} [\log \frac{q(z)}{p(z)}] + \log p(x) - E_{z \sim q(z)} [\log p(x|z)]$$

$$\approx \frac{1}{K} \sum_{i=0}^K [\log \frac{q(z_i)}{p(z_i)}]_{z_i \sim q(z)} + \log p(x) - \frac{1}{K} \sum_{i=0}^K [\log p(x|z_i)]_{z_i \sim q(z)}$$

$$= \frac{1}{K} \sum_{i=0}^K [\log q(z_i) - \log p(z_i) - \log p(x|z_i)]_{z_i \sim q(z)}+\log p(x)$$

위와 같이 Monte Carlo Method로서 식을 해결하면, \(q(z) (\approx p(z|x))\)를 원하는 Distribution으로서 정할 수 있다. (E.X.) 동전던지기에서는 Posterior가 Beta-Distribution일 것 이다.)
하지만, 실제 해결해야하는 문제에서는 Posterior를 구하기 어렵지만, 어떠한 Distribution으로서도 나타낼 수 있게 된다.

Variational Inference with SGD
VI를 해결하는 방법으로서 Stochastic Variational Inference (SVI)를 사용하는 방법입니다. 위의식을 미분하기 위하여 먼저, 각각의 Distribution을 다음과 같다고 지정하고 식을 전개하자.

• \(q(z), (\theta_{q} = \mu_q, \sigma_q)\): Normal Distribution
• \(p(z), (\alpha, \beta)\): Beta Distribution

$$\frac{\partial}{\partial \theta_q} D_{KL} (q(z) || p(z|x)) = \frac{\partial}{\partial \theta_q} D_{KL} (q(z) || p(z)) + \frac{\partial}{\partial \theta_q} \log p(x) - \frac{\partial}{\partial \theta_q} E_{z \sim q(z)} [\log p(x|z)]$$

$$= \frac{\partial}{\partial \theta_q} E_{z \sim q(z)} [\log q(z) - \log p(z) - \log p(x|z)]$$

위의 수식을 살펴보게 되면, \(\partial / \partial \theta_{q}\)가 Exception안으로 들어가야 하는데 z자체가 \(\theta_{q}\)에 의존하는 Distribution이므로 미분이 불가능한 것을 알 수 있다.

따라서, z대신에 noise(\(\epsilon\))을 사용하여 z를 나타낸다.

$$z = \mu_q + \sigma_q \epsilon, \epsilon \sim N(0,1)$$

$$\frac{\partial}{\partial \theta_q} D_{KL} (q(z) || p(z|x))$$

$$= \frac{\partial}{\partial \theta_q} E_{\epsilon \sim N(0,1)} [\log q (\mu_q + \sigma_q \epsilon) - \log p(\mu_q + \sigma_q \epsilon) - \log p(x|z = \mu_q + \sigma_q \epsilon)]$$

$$= E_{\epsilon \sim N(0,1)} [\frac{\partial}{\partial \theta_q} \{ \log q(\mu_q + \sigma_q \epsilon) - \log p (\mu_q + \sigma_q \epsilon) - \log p(x|z = \mu_q + \sigma_q \epsilon) \}]$$

$$= \frac{1}{K} \sum_{i=0}^K [\log q(\mu_q + \sigma_q \epsilon) - \log p (\mu_q + \sigma_q \epsilon) - \log p(x|z = \mu_q + \sigma_q \epsilon)]_{\epsilon \sim N(0,1)} $$

$$(\because \text{Using Monte Carlo Method})$$

Vatiational EM algorithm
VI와 SVI모두, \(q(z)\)의 parameter를 학습하는 방식이나, 이는 모두 \(p(z) (\text{prior}), p(x|z) (\text{likelihood})\)를 모두 알 고 있는 경우에 값을 구할 수 있다.

하지만, 실제 Likelihood와 Prior를 모르는 경우도 많이 있습니다. 이를 해결하기 위하여 다음과 같이 Parameter를 설정하고 EM algorithm을 통하여 식을 전개합니다. (\(p(z)\)의 값은 임의로 고정시켜고 지장이 없습니다.)

• \(\theta_{q}\): Parameter of \(q(z)\)
• \(\theta_{l}\): Parameter of \(p(x|z)\)

위의 두 Parameter를 Update하기 위하여 아래와 같은 EM-Algorithm을 사용하게 된다.

• Expectation: \(D_{KL} (q(z) || p(z|x))\)를 줄이는 \(\theta_q\)를 찾는다. (VI or SVI)
• Maximization: E-step에서 찾은 \(\theta_q\)를 고정한 상태에서 \(\log p(x)\)의 lower bound를 최대화 하는 \(p(x|z)\)의 \(\theta_{l}\)을 update한다.

먼저 Exception과정의 최종적인 식은 아래와 같다.

$${ E }_{ x\sim p\left( x \right) }\left[ f(x) \right] \approx \frac { 1 }{ K } \sum _{ i=0 }^{ K }{ { \left[ f({ x }_{ i }) \right] }_{ { x }_{ i }\sim p\left( x \right) } }$$

\(p(x)\)에 대하여 식을 정리하면 아래와 같다.

$$\log p(x) = E_{z \sim p(z)}[\log p(x|z)] - D_{KL} (q(z) || p(z)) + D_{KL} ( q(z) || p(z|x))$$

위의 식에서 \(D_{KL} ( q(z) || p(z|x)\)은 항상 양수의 값이므로, update해야하는 \(p(x|z)\)에 대하여 식을 다시 정리하면 아래와 같다.

$$\log p(x) \ge E_{z \sim q(z)} [\log p(x|z)] - D_{KL} (q(z) || p(z))$$

즉, Evidence \(p(x)\)를 Maximization하는 \(\theta_l\)을 찾는 과정으로 해당 식은 Evidence Lower Bound(ELBO)라고 불리게 된다.

The variational bound

위의 Variance Inference의 식을 이해하게 되면, 이제 VAE의 Loss Function을 이해할 수 있다.
GAN의 Loss Function은 아래와 같다.

$$\log p_{\theta}(x^{(1)}, \ldots, x^{(N)}) = \sum_{i=1}^N \log p_{\theta} (x^{(i)}) , (\because \text{Monte Carlo sampling})$$

$$\log p_{\theta} (x^{(i)}) = D_{KL} (q_{\phi} (z|x^{(i)}) || p_{\theta} (z|x^{(i)})) + L(\theta, \phi, x^{(i)})$$

$$\log p_{\theta}(x^{(i)}) \ge L(\theta, \phi, x^{(i)}) = E_{q_{\phi}(z|x)} [-\log q_{\phi}(z|x^{(i)}) + \log p_{\theta}(x^{(i)}|z)]$$

$$ L(\theta, \phi, x^{(i)}) = E_{q_{\phi}(z|x^(i))} [\log p_{\theta}(x^{(i)}|z)] - D_{KL} (q_{\phi} (z|x^{(i)}) || p_{\theta}(z)), (\because \text{Vatiational EM algorithm})$$

위에 대한 식을 수식적으로 이해하는데에는 어렵지 않다.
이러한 위의 식에서 각각의 수식의 Term은 아래와 같이 이해하면 이해하기가 쉽다.

그림 출처: hugrypiggykim Blog

위의 식에서 문제가 되는 Term은 \(E_{q_{\phi}(z|x^(i))} [\log p_{\theta}(x^{(i)}|z)]\)이다.
\(E_{q_{\phi}(z|x^(i) )} (\cdot)\)을 살펴보게 되면, \(q(z|x)\)에서 여러개를 sampling하면 되나, backward에서는 sampling에대한 Gradient를 전파하지 못한다는 문제가 발생하게 된다.

이러한 문제 해결방법을 위하여 해당 논문에서는 “reparameterization trick”을 사용하였다.

Solution 1-st Term, Gaussian Case

위에서 구한 수식은 다시한번 살펴보면 아래와 같다.

$$ L(\theta, \phi, x^{(i)}) = - D_{KL} (q_{\phi} (z|x^{(i)}) || p_{\theta}(z))) + E_{q_{\phi}(z|x^(i))} [\log p_{\theta}(x^{(i)}|z)] $$

위의 수식은 \(D_{KL} (q_{\phi} (z|x^{(i)}) || p_{\theta}(z)))\) (1-st Term: Regularization)과 \(E_{q_{\phi}(z|x^(i))} [\log p_{\theta}(x^{(i)}|z)]\) (2-nd Term: Reconstruction Error)으로서 나눌 수 있다.

위에 수식에서 문제가 되는 것은 Sampling을 수행해야하는 2-nd Term이고 1-st Term은 아래와 같이 풀어서 사용할 수 있다.

• \(p_{\theta}(z) = N(0,I)\): Prior
• \(q_{\phi}(z|x^{(i)})\): Posterior approximation (Gaussian)
• \(u_i, \sigma_i\): i-th element mean and variance of posterior approximation
• \(u_j, \sigma_j\): j-th element mean and variance of posterior approximation
• \(J\): Dimension of \(z\)

또한 위의 식을 쉽게 풀기 위하여 \(q_{\phi}(z|x^{(i)}), p_{\theta}(z)\)를 \(q(x), p(x)\)로서 표현하고 각각의 평균과 분산을 \(\mu_1, \sigma_1, \mu_2, \sigma_2\)이고, univariate Gaussian이라 생각하면 아래와 같이 식을 쓸 수 있다.

$$D_{KL} (q (x) || p(x))$$

$$=\int q(x) (\log q(x) - \log p(x)) dx$$

$$=\int [-\frac{1}{2} \log (2\pi) - \log (\sigma_1) - \frac{1}{2}(\frac{(x-\mu_1)}{\sigma_1})^2 + \frac{1}{2} \log (2\pi) + \log (\sigma_2) + \frac{1}{2}(\frac{(x-\mu_2)}{\sigma_2})^2] \times \frac{1}{\sqrt{2\pi}\sigma_1} \text{exp} [-\frac{1}{2} (\frac{x - \mu_1}{\sigma_1})^2] dx$$

$$= \int \{ \log(\frac{\sigma_2}{\sigma_1}) + \frac{1}{2} [(\frac{x - \mu_2}{\sigma_2})^2 - (\frac{x - \mu_1}{\sigma_1})^2] \} \times \frac{1}{\sqrt{2\pi}\sigma_1} \text{exp} [-\frac{1}{2} (\frac{x - \mu_1}{\sigma_1})^2] dx$$

$$E \{ \log(\frac{\sigma_2}{\sigma_1}) + \frac{1}{2} [(\frac{x - \mu_2}{\sigma_2})^2 - (\frac{x - \mu_1}{\sigma_1})^2] \} (\because \int \frac{1}{\sqrt{2\pi}\sigma_1} \text{exp} [- \frac {1}{2} (\frac{x - \mu_1}{\sigma_1})^2] dx = 1)$$

$$= \log (\frac{\sigma_2}{\sigma_1}) + \frac{1}{2\sigma_2^2} E \{ (X-\mu_2)^2 \} - \frac{1}{2\sigma_1^2} E \{ (X-\mu_1)^2 \}$$

$$= \log (\frac{\sigma_2}{\sigma_1}) + \frac{1}{2\sigma_2^2} E \{ (X-\mu_2)^2 \} - \frac{1}{2} (\because E \{ (X-\mu_1)^2 \} = \sigma_1^2)$$

This expectation term can be reformulated,

$$(X - \mu_2)^2 = (X - \mu_1 + \mu_1 - \mu_2)^2 = (X-\mu_1)^2 + 2(X-\mu_1)(\mu_1 - \mu_2) + (\mu_1 - \mu_2)^2$$

Hence,

$$= \log(\frac{\sigma_2}{\sigma_1}) + \frac{1}{\sigma_2^2} [E\{ (X-\mu_1)^2 \} + 2(\mu_1 - \mu_2) E\{ (X-\mu_1) \} + (\mu_1-\mu_2)^2]-\frac{1}{2}$$

$$= \log (\frac{\sigma_2}{\sigma_1}) + \frac{\sigma_1^2 (\mu_1 - \mu_2)^2}{2\sigma_2^2} - \frac{1}{2}$$

$$ -\log (\sigma_1) + \frac{\sigma_1^2 + \mu_1^2}{2} -\frac{1}{2}(\because, \mu_2=0, \sigma_2=1)$$

최종적인 위의 식을 J dimension의 multivariate Gaussian이라 생각하면 최종적인 식은 다음과 같이 적을 수 있다.

$$-D_{KL} (q_{\phi} (z|x^{(i)}) || p_{\theta}(z))) = \frac{1}{2} \sum_{j=1}^J (1 + \log ((\sigma_j)^2)-(\mu_j)^2 - (\sigma_j)^2)$$

The reparameterization trick

최종적인 Loss Function을 생각해보면 아래와 같다.

$$ L(\theta, \phi, x^{(i)}) = - D_{KL} (q_{\phi} (z|x^{(i)}) || p_{\theta}(z))) + E_{q_{\phi}(z|x^(i))} [\log p_{\theta}(x^{(i)}|z)] $$

위에 수식에서 문제가 되는 것은 Sampling을 수행해야하는 2-nd Term은 \(g_{\phi}(\epsilon, x)\)라는 미분 가능한 함수와 보조 noise variable \(\epsilon\)으로 나타낼 수 있다.

$$\tilde{z} = g_{\phi}(\epsilon, x) \text{ with } \epsilon \sim p(\epsilon)$$

$$E_{q_{\phi}(z|x^(i))} [f(z)] = E_{p(\epsilon)} [ f(g_{\phi}(\epsilon, x^{(i)})) ] = \frac{1}{L} \sum_{l=1}^{L} f(g_{\phi}(\epsilon^{(l)}, x^{(i)})) \text{, where } \epsilon^{(l)} \sim p(\epsilon) $$

$$(\because \text{Monte Carlo sampling})$$

위에서 \(q_{\phi}(z|x^{(i)})\)는 Gaussian Distribution이였습니다. 이것을 다시 나타내면 \(Q(Z|X) = N(\mu(X), \sum(X))\)이고 이를 \(\epsilon \sim N(0,I)\)로서 sampling한 형태로 나타내게 되면, \(z = \mu(X) + \sum^{(1/2)} * \epsilon\)로 변환되는 것을 알 수 있습니다.

즉, 문제가 되었던 stochastic인 부분인 \(q_{\phi} (z|x)\)을 backprogagation과 상관없는 \(\epsilon \sim p(\epsilon)\)으로서 나타내어, deterministic한 \(g_{\phi}(\epsilon, x)\)으로 표현하여 \(z = \mu(X) + \sum^{(1/2)} * \epsilon\)값으로서 표현할 수 있다.

이를 그림으로 보면 아래와 같다.

그림 출처: 초짜 대학원생의 입장에서 이해하는 Auto-Encoding Variational Bayes (VAE) (3)

각각의 정리한 식을 모두 적용하면 최종적인 식은 다음과 같다.

$$ L(\theta, \phi, x^{(i)}) = - D_{KL} (q_{\phi} (z|x^{(i)}) || p_{\theta}(z))) + E_{q_{\phi}(z|x^(i))} [\log p_{\theta}(x^{(i)}|z)] $$

$$= \frac{1}{2} \sum_{j=1}^J (1 + \log ((\sigma_j)^2)-(\mu_j)^2 - (\sigma_j)^2) + \frac{1}{L} \sum_{l=1}^{L} f(g_{\phi}(\epsilon^{(l)}, x^{(i)}))$$

$$\text{, where } z^{(i,l)} = g_{\phi}(\epsilon^{(i,l)}, x^{(i)}) \text{ and } \epsilon^{(l)} \sim p(\epsilon) \text{ and } J = \text{Dimension of }z$$

Appendix 1. \(\log p_{\theta}(x^{(i)}|z)\)

\(\log p_{\theta}(x^{(i)}|z)\)을 실제 예제에 대입하여 저자들은 아래와 같이 Loss Function을 예시를 들었다.

Appendix 2. \(q_{\phi} (z|x), g_{\phi}(\cdot), \epsilon \sim p(\epsilon)\)

위의 수식을 이해할때에는 모두 Gaussian Distribution으로서 가정하고 식을 전개하고 알아보았다.
각각에 대하여 어떤 Distribution으로 두어야되는지에 대해서 저자는 다음과 같이 설명하고 있다.

Pytorch Code

-Code 참조: cumulu-s blog

Model

• x: samples (\(X = \{x^{(i)}\}_{i=1}^N\))
• encode(self, x): Encoder (\(q_{\phi} (z|x)\))
• decode(self, z): Decoder (\(p_{\theta} (x|z)\))
• self.fc31(h2): mean of z (\(\mu\))
• self.fc32(h2): log variance of z (\(\log (\sigma)\))
• eps = torch.randn_like(std): \(\epsilon \sim N(0, I)\)
• reparameterize(self, mu, logvar): \(z = \mu(X) + \sum^{(1/2)} * \epsilon\)

# VAE model
class VAE(nn.Module):
    def __init__(self, image_size, hidden_size_1, hidden_size_2, latent_size):
        super(VAE, self).__init__()

        self.fc1 = nn.Linear(image_size, hidden_size_1)
        self.fc2 = nn.Linear(hidden_size_1, hidden_size_2)
        self.fc31 = nn.Linear(hidden_size_2, latent_size)
        self.fc32 = nn.Linear(hidden_size_2, latent_size)

        self.fc4 = nn.Linear(latent_size, hidden_size_2)
        self.fc5 = nn.Linear(hidden_size_2, hidden_size_1)
        self.fc6 = nn.Linear(hidden_size_1, image_size)

    def encode(self, x):
        h1 = F.relu(self.fc1(x))
        h2 = F.relu(self.fc2(h1))
        return self.fc31(h2), self.fc32(h2)

    def reparameterize(self, mu, logvar):
        std = torch.exp(0.5 * logvar)
        eps = torch.randn_like(std)
        return mu + std * eps

    def decode(self, z):
        h3 = F.relu(self.fc4(z))
        h4 = F.relu(self.fc5(h3))
        return torch.sigmoid(self.fc6(h4))

    def forward(self, x):
        mu, logvar = self.encode(x.view(-1, 784))
        z = self.reparameterize(mu, logvar)
        return self.decode(z), mu, logvar

Loss Function

$$ L(\theta, \phi, x^{(i)}) = - D_{KL} (q_{\phi} (z|x^{(i)}) || p_{\theta}(z))) + E_{q_{\phi}(z|x^(i))} [\log p_{\theta}(x^{(i)}|z)] $$

$$= \frac{1}{2} \sum_{j=1}^J (1 + \log ((\sigma_j)^2)-(\mu_j)^2 - (\sigma_j)^2) + \frac{1}{L} \sum_{l=1}^{L} f(g_{\phi}(\epsilon^{(l)}, x^{(i)}))$$

$$\text{, where } z^{(i,l)} = g_{\phi}(\epsilon^{(i,l)}, x^{(i)}) \text{ and } \epsilon^{(l)} \sim p(\epsilon) \text{ and } J = \text{Dimension of }z$$

• -0.5 * torch.sum(1 + logvar - mu.pow(2) - logvar.exp()): \(\frac{1}{2} \sum_{j=1}^J (1 + \log ((\sigma_j)^2)-(\mu_j)^2 - (\sigma_j)^2)\)
• F.binary_cross_entropy(recon_x, x.view(-1, 784), reduction = 'sum'): \(\sum_{i=1}^D x_i \log y_i + (1-x_i) \cdot \log (1-y_i), (\because \log p(x|z) \text{ is Bernoulli})\)

def loss_function(recon_x, x, mu, logvar):
    BCE = F.binary_cross_entropy(recon_x, x.view(-1, 784), reduction = 'sum')
    KLD = -0.5 * torch.sum(1 + logvar - mu.pow(2) - logvar.exp())
    return BCE, KLD