Pytorch-GAN
GAN
생성적 적대 신경망(GAN)은 2014년에 처음 소개된 방식으로서 Generative Adversarial network이다.
- Generative(생성적): 데이터 자체를 생성한다.
- Adversarial(적대적): 적대란 대립하거나 상반되는 관계를 뜻한다. GAN에서는 생성네트워크와 구분 네트워크간의 상반되는 목적함수로 인해 적대성이 생기게 된다.
- Network: 생성자와 구분자의 구조가 인공 신경망의 형태를 이룬다.
GAN에서 가장 중요한 것은 생성 네트워크와 구분 네트워크로서 상반되는 네트워크를 구성한다는 것 이다.
예를 들면 다음과 같다.
위조지폐를 만드는 사람(생성 네트워크)과 위조지폐 감별사(구분 네트워크)가 있다.
생성자가 처음에 만든 지폐는 쉽게 감별이 되겠지만 감별사를 속이는 것을 목표로 계속 학습하고 생성하다 보면 점점 감별사가 구분하기 어려운 수준까지 생성이 가능해진다는 것 이다.
이때 위조지폐 생성자는 자신이 생성한 지폐가 진짜로 판별되기 원하고, 감별사는 가짜 지폐를 가짜로 판별하는 것을 목표로 하기 때문에 여기에서 적대성이 생기게 된다.
위와 같은 2가지의 상반되는 네트워크는 아래 그림과 같다.
위의 그림을 설명하기 위해서 다음과 같은 가정을 해보자.
- D(x): Data를 실제 데이터는 1, 생성 데이터는 0으로 판별하는 함수
- G(x): Data를 생성하는 함수
- x: 실제 데이터
- z: Noise
위의 그림과 GAN의 최종적인 목적은 2개의 Network에 따라서 다음과 같이 구분될 수 있다.
구분자의 입장
최종적인 목적은 D(x) = 1, D(G(z)) = 0, 으로서 학습되는 것 즉, 실제 데이터는 1, 만들어진 데이터는 0 으로서 판별되는 것을 목표로 한다.
생성자 입장
최종적인 목적은 D(G(z)) = 1 로서 만들어진 데이터를 1로서 판별되는 것을 목표로 한다.
D(G(z))에 대하여 2개의 Network가 상반되는 목표를 가지는 것을 알 수 있다.
Adversarial Nets
위의 설명은 다음과 같이 정의 될 수 있다.
$$ \underset{G}{min} \underset{D}{max}V(D,G) =$$
$$\mathbb{E}_{x\text{~}P_{data}(x)}[logD(x)] + \mathbb{E}_{z\text{~}P_{z}(z)}[log(1 - D(G(z)))]$$
$$\mathbb{E}: \text{기대값}$$
$$x\text{~}P_{data}(x): \text{x를 실제 data의 분포에서 샘플링}$$
$$z\text{~}P_{z}(z): \text{z를 Noise의 분포에서 샘플링}$$
위에서 쓰여진 식을 D, G에 관해 나누어서 생각해보자
구분자
$$ \underset{D}{max}V(D,G) = $$
$$\mathbb{E}_{x\text{~}P_{data}(x)}[logD(x)] + \mathbb{E}_{z\text{~}P_{z}(z)}[log(1 - D(G(z)))]$$
위에서 정의한 구분자의 목적은 실제 데이터는 1, 만들어진 데이터는 0 으로서 판별되는 것이다.
이에 연관되어
$$\underset{D}{max}V(D,G) = $$
$$\mathbb{E}_{x\text{~}P_{data}(x)}[logD(x)] + \mathbb{E}_{z\text{~}P_{z}(z)}[log(1 - D(G(z)))]$$
에 넣어서 생각을 해보게 되면 D(x) = 1, D(G(z)) = 0, 으로서 학습되는 것이다.
생성자
$$ \underset{G}{min}V(D,G) = $$
$$\mathbb{E}_{x\text{~}P_{data}(x)}[logD(x)] + \mathbb{E}_{z\text{~}P_{z}(z)}[log(1 - D(G(z)))]$$
위에서 정의한 생성자의 목적은 만들어진 데이터를 1로서 판별되는 것 이다. 위의 목적에 맞게 다시 식을 작성하면 다음과 같다.
$$ \underset{G}{min}V(D,G) = \mathbb{E}_{z\text{~}P_{z}(z)}[log(1 - D(G(z)))]$$
이에 연관되어 \(\underset{G}{min}V(D,G) = \mathbb{E}_{z\text{~}P_{z}(z)}[log(1 - D(G(z)))]\)에 넣어서 생각을 해보게 되면 D(G(z)) = 1 으로서 학습되는 것이다.
참고사항으로서 구분자와 생성자의 식을 분리하게 됨으로서 식을 다음과 같이 바꿀 수 있다.
$$ \underset{G}{max}V(D,G) = \mathbb{E}_{z\text{~}P_{z}(z)}[log( D(G(z)))]$$
위와 같이 식을 바꾸는 이유는 다음과 같다.
처음 Noise로서 생성하는 Image는 Random한 Image로서 구분자가 너무 쉽게 Real Image와 구별할 수 있게 되어서 값이 너무 작게 나와서 Trainning의 시간이 매우 길어지게 된다.
하지만 위와 같이 식을 바꿈으로 인하여 Fixed Point를 얻게 되면서도 Gradint의 값을 크게 줄 수 있다는 장점이 생기게 된다.
논문에서의 이러한 상황을 그림으로서 표현하면 다음과 같다.
위의 그림에서의 의미는 각각 다음과 같다.
- 검은 점선: 실제 데이터의 분포(Data generating Distribution), \(p_{data}\)
- 녹색 점선: 생성된 데이터의 분포(Discriminator Distribution), \(p_{g}\)
- 파란 점선: 판별자가 데이터의 판별 결과 분포(Generative Distribution), \(D(x)\)
(a): 처음 시작할 때는 \(p_{data}\)와 \(p_{g}\)의 분포는 매우 다른 것을 알 수 있다.
(b), (c): 이러한 상황에서
$$ \underset{G}{min} \underset{D}{max}V(D,G) =$$
$$\mathbb{E}_{x\text{~}P_{data}(x)}[logD(x)] + \mathbb{E}_{z\text{~}P_{z}(z)}[log(1 - D(G(z)))]$$
을 학습하다 보면 D(x)의 파란점선이 점점 smooth하고 잘 구별하는 Distribution이 만들어 진다.
(d): Trainning의 최종적인 Distribution의 모양은 \(p_{data} = p_{g}\)으로서 \(D(x) = \frac{1}{2}\)의 값을 가지는 것을 알 수 있다.
최종적인 목적으로서 앞에서 정의한 식
$$ \underset{G}{min} \underset{D}{max}V(D,G) =$$
$$\mathbb{E}_{x\text{~}P_{data}(x)}[logD(x)] + \mathbb{E}_{z\text{~}P_{z}(z)}[log(1 - D(G(z)))]$$
의 해결하기 위해서는 \(p_{data} = p_{g}\)으로서 \(D(x) = \frac{1}{2}\)의 값을 가지는 것을 찾는 문제로서 생각할 수 있다.
Theoretical Results
위에서 \(p_g = p_{data}\)에서 최적의 global optimam을 가진다고 그림으로서 알아보았다.
그렇다면 \(p_g = p_{data}\)에서 최적의 해가 1개인지 다른 해가 있는지를 알아보는 과정이 필요하다.
그러한 과정을 위하여 먼저 선수 과정으로 알아야 하는 수식에 대해서 알아보자.
사전지식
본격적인 수식에 들어가기 전에 수식을 이해하기 위한 사전지식이 요구된다.
요구되는 사전지식은 아래와 같다.
정보량
정보량이란 확률 p를 가지는 사건 A의 정보를 정의한다.
$$I(m) = log(\frac{1}{p(m)}) = - log(p(m))$$
Entropy
엔트로피란 어떤 다수의 메세지들에 대해서 각각의 정보량을 평균한 값을 의미한다.
2가지의 Data의 형태에 따른 각각의 다른 수식에 대해서 알아보자.
(1) Discrete
$$H(M) = E\text{[}I(M)\text{[} = \sum_{m \in M}p(m)I(m) = -\sum_{m \in M}p(m)log p(m)$$
(2) Continuous
$$H(X) = E\text{[}I(M)\text{[} = \int p(x)I(x)dx = - \int p(x)log(p(x))dx$$
추가적인 자세한 내용은 아래를 참조하자.
Kullback-Leibler divergence(KL-Divergence)
KL-Divergenc는 어떤 확률 분포 p(x)와 q(x)의 유사한 정도를 계산하는 방법이다.
KL-Divergence는 그 값이 작을 수록 두 분포가 유사하다는 의미를 가지고 0이되면 두 분포가 같다는 의미를 가진다.
KL-Divergence를 계산하기 위해서는 Cross Entropy를 사용하여 p를 q로 설명하는 정보량을 뜻하는 Cross Entropy에서 p가 자기자신을 설명하는 정보량인 p의 엔트로피의 차이가 KL-Divergence가 된다.
즉 두 확률분포의 Cross Entropy의 값과 자기자신의 Entropy의 값이 같으면 두 확률분포는 같다는 Idea에서 시작하는 수식이다.
$$D_{KL}(p||q) = H(p,q) - H(p)$$
$$= -\sum_{x \in X}p(x)log(q(x)) - (-\sum_{x \in X}p(x)log(p(x)))$$
$$= \sum_{x \in X}p(x)(log(p(x)) - log(q(x)))$$
$$= \sum_{x \in X}p(x)log\frac{p(x)}{q(x)}$$
참조:reniew 블로그
Global Optimality of \(p_g = p_{data}\)
먼저 다음과 같은 가정을 하자
Proposition 1. for G fixed, the optimal discriminator D is
$$D_G^*(x) = \frac{p_{data}(x)}{p_{data}(x) + p_g(x)}$$
위의 결과는 아래와 같은 과정으로서 이루워 진다.
$$V(G,D) = \mathbb{E}_{x \text{~} p_{data}(x)}\text{[}logD(x)\text{]} + \mathbb{E}_{x \text{~} p_{z}(z)}\text{[}1 - logD(G(z))\text{]}$$
$$= \int_x p_{data}(x) log(D(x)) dx + \int_z p_{z}(x) log(1 - D(G(z))) dz$$
$$= \int_x p_{data}(x) log(D(x)) dx + p_g log(1-D(x))$$
위의 식을 간단히 하기 위하여 다음과 같이 치환하여 생각을 해보자.
$$y = alog(y) + blog(1-y)$$
$$y\prime = \frac{a}{y} - \frac{b}{1-y} = \frac{a}{y} = \frac{b}{y - 1}$$
$$= \frac{a(y-1) + by}{y(y-1)}$$
$$= \frac{ay -a + by}{y(y-1)}$$
위의 조건에서 만약 \(y \neq 0,1\)이라면 \(y\prime = 0\)의 조건은
$$ay - a + by = 0 $$
$$y = \frac{a}{a+b}$$
위에서 얻은 식에 \(a = p_{data}, b=p_g\)를 대입하게 되면
$$D_G^*(x) = \frac{p_{data}(x)}{p_{data}(x) + p_g(x)}$$
위에서 선언한 식을 알 수 있다.
최종적으로 얻고자 하는 global minumum을 \(C(G)\)라 하면 다음과 같은 식을 유도할 수 있다.
$$C(G) = \underset{D}{max}V(G,D)$$
$$= \mathbb{E}_{x \text{~} p_{data}}\text{[}logD^{*}_{G}(x)\text{]} + \mathbb{E}_{z \text{~} p_{z}}\text{[}1 - logD^{*}_{G}(G(z))\text{]}$$
$$= \mathbb{E}_{x \text{~} p_{data}}\text{[}logD^{*}_{G}(x)\text{]} + \mathbb{E}_{x \text{~} p_{g}}\text{[}1 - logD^{*}_{G}(x)\text{]}$$
$$= \mathbb{E}_{x \text{~} p_{data}}\text{[}log\frac{p_{data}(x)}{p_{data}(x)+ p_g(x)}\text{]}$$
$$ + \mathbb{E}_{x \text{~} p_g}\text{[}1 - log\frac{p_{data}(x)}{p_{data}(x) + p_g(x)}\text{]}$$
위에서 증명한 식을 사용하여 이제 실질적인 main theorem을 증명해 보자.
Theorem 1. The global minimum of the virtual training criterion C(G) is achieved if and only if \(p_g = p_{data}\) At that point, C(G) achieves the value -log4
가장 최적의 해가 되는 때는 \(p_{data} = p_g\)이고 이때의 \(D^{*}_{G}(x) = \frac{1}{2}\)라고 가장 먼저 그림으로서 증명하였다.
이러한 값을 Proposition 1 에서 얻은 최종적인 값에 대입하게 되면 다음과 같다.
$$C(G) = \mathbb{E}_{x \text{~} p_{data}}\text{[}-log(2)\text{]} + \mathbb{E}_{x \text{~} p_g}\text{[}-log(2)\text{]} = -log(4)$$
위의 식의 결과를 좀더 정리하면 다음과 같다.
$$C(G) = C(G) + log(4) - log(4)$$
$$= \mathbb{E}_{x \text{~} p_{data}}\text{[}log\frac{p_{data}(x)}{p_{data}(x)+ p_g(x)}\text{]}$$
$$ + \mathbb{E}_{z \text{~} p_z}\text{[} log\frac{p_{data}(x)}{p_{data}(x) + p_g(x)}\text{]} +log(4) - log(4)$$
$$= \mathbb{E}_{x \text{~} p_{data}}\text{[}log\frac{p_{data}(x)}{p_{data}(x) + p_g(x)}\text{]} + \mathbb{E}_{z \text{~} p_z}\text{[} log\frac{p_{data}(x)}{p_{data}(x) + p_g(x)}\text{]}$$
$$+log(4) - log(4) +log(2) + log(2) - log(4)$$
$$= \mathbb{E}_{x \text{~} p_{data}}\text{[}log\frac{2p_{data}(x)}{p_{data}(x)+ p_g(x)}\text{]}$$
$$ + \mathbb{E}_{z \text{~} p_z}\text{[} log\frac{2p_{data}(x)}{p_{data}(x) + p_g(x)}\text{]}- log(4)$$
위의 식에서 \(\mathbb{E}_{x \text{~} p_{data}}\text{[}log\frac{2p_{data}(x)}{p_{data}(x) + p_g(x)}\text{]}\)과 \(\mathbb{E}_{z \text{~} p_z}\text{[} log\frac{2p_{data}(x)}{p_{data}(x) + p_g(x)}\text{]}- log(4)\)에 각각 KL-Divergence를 적용하면 다음과 같은 수식이 나오게 된다.
$$C(G) = KL(p_{data} || \frac{p_{data}+p_g}{2})$$
$$+ KL(p_{g} || \frac{p_{data}+p_g}{2}) - log(4)$$
$$= 2JSD(p_{data}||p_g) - log(4)$$
$$\because JSD(P||Q) = \frac{1}{2}D_{KL}(P||M) + \frac{1}{2}D_{KL}(Q||M)$$
$$C(G) = -log(4) = -log(4) + 2JSD(p_{data}||p_g)$$
$$\therefore JSD(p_{data}||p_g) = 0$$
위의 식에서 KL-Divergence에서도 얘기하였지만 KL-Divergence는 그 값이 작을 수록 두 분포가 유사하다는 의미를 가지고 0이되면 두 분포가 같다는 의미를 가진다.
따라서 \(JSD(p_{data}||p_g) = 0\)의 값을 가지기 위해서는
\(p_{data} = p_g\)
위의 최종적인 식이 유일한 최적의 global optimam인 것을 알 수 있다.
결과적으로 앞서 정의한 global optimam을 찾으면 generator가 만드는 probatility distribution(\(p_g\), generator에서 만든 data의 분포)와 data distribution(\(p_{data}\), 실제 데이터의 분포)가 정확히 일치하도록 할 수 있다.
하지만, 이러한 Model을 사용하는 것이 global optimam을 잘 찾아가는 것인거와는 다른 문제이다.
즉, 해를 정의하는 것과 그 해를 찾아갈 수 있는 것과는 별개의 문제이다.
Convergence of Algorithm1
Proposition 2. If G and D have enough capacity, and at each step of Algorithm1, the discriminator is allowed to reach its optimum given G, and \(p_g\) is updated so as to improve the criterion
$$\mathbb{E}_{x \text{~} p_{data}}\text{[}logD^{*}_{G}(x)\text{]} + \mathbb{E}_{x \text{~} p_g}\text{[} log(1 - D^{*}_{G}(x))\text{]}$$
then \(p_g\) converges to \(p_{data}\)
논문에서의 가장 첫 증명은 \(V(G,D) = U(p_g,D)\) as a function of \(p_g\) as done in the above criterion. Note that \(U(p_g,D)\) is convex in \(p_g\)
즉 \(U(p_g,D)\)가 \(p_g\)에 대하여 Convex하다는 것이 가장 중요시 된다.
위의 식을 살펴보게 되면 다음과 같다.
$$V(G,D) = U(p_g,D)$$
$$= \mathbb{E}_{x \text{~} p_{data}}\text{[}log\frac{p_{data}(x)}{p_{data}(x) + p_g(x)}\text{]} + \mathbb{E}_{x \text{~} p_g}\text{[} log\frac{p_{g}(x)}{p_{data}(x) + p_g(x)}\text{]}$$
위의 식을 \(p_g\)에 나타내기 위하여 \(p_{data}\)를 상수로 잠시 치환하자면 다음과 같은 식이 나오게 된다.
$$U(p_g,D) = \mathbb{E}_{x \text{~} p_{data}}\text{[}log\frac{\alpha}{\alpha + p_g(x)}\text{]} + \mathbb{E}_{x \text{~} p_g}\text{[} log\frac{p_g(x)}{\alpha + p_g(x)}\text{]}$$
로그함수의 그래프를 살펴보면 아래와 같다.

Log 함수는 Concave하다는 것을 알 수 있다.
따라서 다음과 같은 식이 성립한다는 것을 알 수 있다.
$$\frac{\alpha}{\alpha + p_g(x + t)} > \frac{\alpha}{\alpha + p_g(x)}$$
$$p_g(x) > p_g(x + t)$$
$$\therefore U(p_g,D) \text{ is Convex in } p_g$$
\(U(p_g,D) \text{ is Convex in } p_g\)가 Convex하다는 가정을 하고 아래와 같이 수식을 치환한다고 하면
$$\partial(sup_DU(p_g,D)) = \partial f$$
\(sup:\) supremum(상한) 또는 최소 상계(least upper bound)로서 집합의 모든 상계 z에 대해 z0≤z를 만족하는 값. 즉, min(z)를 의미한다.
$$\partial f_{D^*(p_g)} \in \partial f$$
위의 식을 만족하게 된다.
즉 \(U(p_g,D) \text{ is Convex in } p_g\)가 Convex하기 때문에 \(\underset{G}{min} \underset{D}{max}V(D,G) = \mathbb{E}_{x\text{~}P_{data}(x)}[logD(x)] + \mathbb{E}_{z\text{~}P_{z}(z)}[log(1 - D(G(z)))]\)에서 \(\underset{G}{min}\)을 수행하여 만족하는 \(p_g\)을 구할 수 있다.
최종적인 결과 로서 위에
Theorem 1. The global minimum of the virtual training criterion C(G) is achieved if and only if \(p_g = p_{data}\) At that point, C(G) achieves the value -log4
에서 Global Optima는 1개라는 정의를 하였으므로
\(p_g\)를 Update하여 \(p_g -> p_{data}\)을 만족시킬 수 있는 것을 알 수 있다.
참고사항(Convex)
Convex function은 convex한 function을 의미한다. 이때의 convex는 한국어로 옮기면 볼록 이라는 의미를 가지게 된다.
Convex function의 조건은 다음과 같다.
$$f(tx + (1-t)y) <= tf(x) + (1-t)f(y)$$
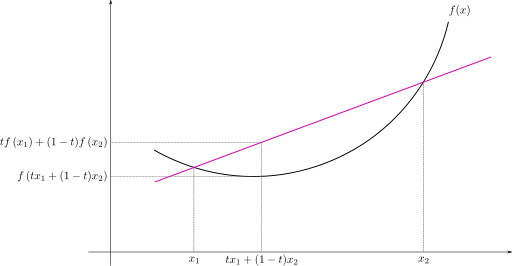
Convex function이 좋은 이유는 반드시 optimal한 값이 하나 밖에 존재하지 않는 다는 것 이다.
Concave의 경우 Convex와 반대의 성질을 가지고 있다.
Convex의 자세한 내용
Model 구현
1. Import required libraries
1
2
3
4
5
6
7
8
9
10
11
12
13
# 단순한 GAN 모델 생성 및 OrderedDict 사용법
import os
import torch
import torch.nn as nn
import torch.utils as utils
import torch.nn.init as init
import torchvision.utils as v_utils
import torchvision.datasets as dset
import torchvision.transforms as transforms
import numpy as np
import matplotlib.pyplot as plt
from collections import OrderedDict
2. Hyperparameter setting
1
2
3
4
5
6
7
8
9
# Set Hyperparameters
# change num_gpu to the number of gpus you want to use
epoch = 50
batch_size = 512
learning_rate = 0.0002
num_gpus = 1
z_size = 50
middle_size = 200
3. Data Setting
1
2
3
4
5
6
7
# Download Data
mnist_train = dset.MNIST("./", train=True, transform=transforms.ToTensor(), target_transform=None, download=True)
# Set Data Loader(input pipeline)
train_loader = torch.utils.data.DataLoader(dataset=mnist_train,batch_size=batch_size,shuffle=True,drop_last=True)
4. Generator
OrderDict를 사용하게 되면 Dict와 달리 순서가 저장되는 딕셔너리 이다.
Generator는 Noise를 Input으로 받아서 Input Data와 비슷한 Data를 만드는 것을 목표로 한다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
# Generator receives random noise z and create 1x28x28 image
# OrderedDict를 사용해 해당 연산의 이름을 지정할 수 있습니다.
class Generator(nn.Module):
def __init__(self):
super(Generator,self).__init__()
self.layer1 = nn.Sequential(OrderedDict([
('fc1',nn.Linear(z_size,middle_size)),
('bn1',nn.BatchNorm1d(middle_size)),
('act1',nn.ReLU()),
]))
self.layer2 = nn.Sequential(OrderedDict([
('fc2', nn.Linear(middle_size,784)),
#('bn2', nn.BatchNorm1d(784)),
('tanh', nn.Tanh()),
]))
def forward(self,z):
out = self.layer1(z)
out = self.layer2(out)
out = out.view(batch_size,1,28,28)
return out
5. Discriminator
구분자는 Input Data와 생성된 Data를 구별하는 역할을 한다.
True는 1, False는 0으로서 구별하기 위하여 최종적인 결과는 Sigmoid를 통하여 계산하게 된다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
# Discriminator receives 1x28x28 image and returns a float number 0~1
# we can name each layer using OrderedDict
class Discriminator(nn.Module):
def __init__(self):
super(Discriminator,self).__init__()
self.layer1 = nn.Sequential(OrderedDict([
('fc1',nn.Linear(784,middle_size)),
#('bn1',nn.BatchNorm1d(middle_size)),
('act1',nn.LeakyReLU()),
]))
self.layer2 = nn.Sequential(OrderedDict([
('fc2', nn.Linear(middle_size,1)),
('bn2', nn.BatchNorm1d(1)),
('act2', nn.Sigmoid()),
]))
def forward(self,x):
out = x.view(batch_size, -1)
out = self.layer1(out)
out = self.layer2(out)
return out
6. Put instances on Multi-gpu
여러대의 GPU 혹은를 사용하기 위해서는 Pytorch에서는 nn.DataParallel()사용
특정 Device를 지정하기 위해서는 devices_ids=[0,1,2, …]처럼 Device의 번호를 인수로서 담아서 넣어주면 된다.
만약 적지 않으면 사용 가능한 모든 GPU에 Module이 올라가게 된다.
ex)
1
generator = nn.DataParallel(Generator(),device_ids = [0,1,2,3,4,5])
참고: DataParallel 사용법(Pytorch 공식 사이트)
1
2
3
4
5
device = torch.device('cuda') if torch.cuda.is_available() else torch.device('cpu')
print(device)
generator = nn.DataParallel(Generator()).to(device)
discriminator = nn.DataParallel(Discriminator()).to(device)
7. Check layers
1
2
3
4
5
6
7
# Get parameter list by using class.state_dict().keys()
gen_params = generator.state_dict().keys()
dis_params = discriminator.state_dict().keys()
for i in gen_params:
print(i)
module.layer1.fc1.weight
module.layer1.fc1.bias
module.layer1.bn1.weight
module.layer1.bn1.bias
module.layer1.bn1.running_mean
module.layer1.bn1.running_var
module.layer1.bn1.num_batches_tracked
module.layer2.fc2.weight
module.layer2.fc2.bias
8. Set Loss function & Optimizer
- Loss Function: MSE
- Optimizer: Adam
1
2
3
4
5
6
7
8
# loss function, optimizers, and labels for training
loss_func = nn.MSELoss()
gen_optim = torch.optim.Adam(generator.parameters(), lr=learning_rate,betas=(0.5,0.999))
dis_optim = torch.optim.Adam(discriminator.parameters(), lr=learning_rate,betas=(0.5,0.999))
ones_label = torch.ones(batch_size,1).to(device)
zeros_label = torch.zeros(batch_size,1).to(device)
9. Restore Model
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
# model restore if any
try:
generator, discriminator = torch.load('./model/vanilla_gan.pkl')
print("\n--------model restored--------\n")
except:
print("\n--------model not restored--------\n")
pass
try:
os.mkdir("./model")
except:
pass
try:
os.mkdir("./result")
except:
pass
10. Train Model
Generator에서 Input Data를 받는것이 아니라 Noise를 Input으로 받는다는 가정을 하였기 때문에 Input Data -> Noise로 변환하여 Generator에 Input으로 넣는 과정이 필요하다.
z = init.normal_(torch.Tensor(batch_size,z_size),mean=0,std=0.1).to(device)
최종적인 식
$$ \underset{G}{min} \underset{D}{max}V(D,G) = \mathbb{E}_{x\text{~}P_{data}(x)}[logD(x)] + \mathbb{E}_{z\text{~}P_{z}(z)}[log(1 - D(G(z)))]$$
구분자
$$ \underset{D}{max}V(D,G) = $$
$$\mathbb{E}_{x\text{~}P_{data}(x)}[logD(x)] + \mathbb{E}_{z\text{~}P_{z}(z)}[log(1 - D(G(z)))]$$
생성자
$$ \underset{G}{max}V(D,G) = $$
$$\mathbb{E}_{z\text{~}P_{z}(z)}[log( D(G(z)))]$$
을 각각 적용한다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
# train
for i in range(epoch):
for j,(image,label) in enumerate(train_loader):
image = image.to(device)
# 구분자 학습
dis_optim.zero_grad()
# Fake Data
# 랜덤한 z를 샘플링해줍니다.
z = init.normal_(torch.Tensor(batch_size,z_size),mean=0,std=0.1).to(device)
gen_fake = generator.forward(z)
dis_fake = discriminator.forward(gen_fake)
# Real Data
dis_real = discriminator.forward(image)
# 두 손실을 더해 최종손실에 대해 기울기 게산을 합니다.
dis_loss = torch.sum(loss_func(dis_fake,zeros_label)) + torch.sum(loss_func(dis_real,ones_label))
dis_loss.backward(retain_graph=True)
dis_optim.step()
# 생성자 학습
gen_optim.zero_grad()
# Fake Data
z = init.normal_(torch.Tensor(batch_size,z_size),mean=0,std=0.1).to(device)
gen_fake = generator.forward(z)
dis_fake = discriminator.forward(gen_fake)
gen_loss = torch.sum(loss_func(dis_fake,ones_label)) # fake classified as real
gen_loss.backward()
gen_optim.step()
# model save
if j % 100 == 0:
print(gen_loss,dis_loss)
torch.save([generator,discriminator],'./model/vanilla_gan.pkl')
v_utils.save_image(gen_fake.cpu().data[0:25],"./result/gen_{}_{}.png".format(i,j), nrow=5)
print("{}th epoch gen_loss: {} dis_loss: {}".format(i,gen_loss.data,dis_loss.data))
tensor(0.3454, device='cuda:0', grad_fn=<SumBackward0>) tensor(0.4220, device='cuda:0', grad_fn=<AddBackward0>)
0th epoch gen_loss: 0.3454473614692688 dis_loss: 0.4220327138900757
...
49th epoch gen_loss: 0.3454442322254181 dis_loss: 0.420757532119751
tensor(0.3454, device='cuda:0', grad_fn=<SumBackward0>) tensor(0.4228, device='cuda:0', grad_fn=<AddBackward0>)
49th epoch gen_loss: 0.34544625878334045 dis_loss: 0.42280131578445435
Check Result
학습이 거의 이루워 지지 않은 것을 알 수 있다.
추가적인 방법을 추가하여 학습이 필요한 상태이다.
1
2
3
4
5
6
7
8
9
10
11
from glob import glob
for i in range(epoch):
print(i)
file_list = glob("./result/gen_{}_*.png".format(i))
img_per_epoch = len(file_list)
for idx,j in enumerate(file_list):
img = plt.imread(j)
plt.subplot(1,img_per_epoch,idx+1)
plt.imshow(img)
plt.show()
참조: 원본코드
참조: Image Style Transfer Using Convolutional Neural Networks
참조:reniew 블로그
참조:jaejunyoo 블로그
hwiyong 블로그
참조: 파이토치 첫걸음
코드에 문제가 있거나 궁금한 점이 있으면 wjddyd66@naver.com으로 Mail을 남겨주세요.


Leave a comment