R-회귀분석

회귀분석

회귀분석은 상관분석과 더불어 널리 쓰이는 통계적 방법이다. 상관분석이 상관관계를 알아보기 위함이라면 회귀분석의 경우 인과관계를 파악하는 분석 방법이다.

회귀분석 5가지 조건

• 잔차의 정규성: 잔차가 정규분포 이다.
• 선형성: 설명변수와 반응변수 간의 관계 분포가 선형의 관계를 가진다. 선형성을 띄지 않아야 한다.
• 독립성: 설명변수와 다른 설명변수 간에 상관관계가 적다.
• 잔차의 등분산성: 잔차가 특정한 패턴을 보이지 않는다.
• 다중공선성: 다중회귀 모델에 적용. 3개 이상의 독립변수 간에 강한 상관관계가 있어서는 안된다.

회귀 분석의 종류

1. 단순 회귀분석: 종속변수와 독립변수 사이의 관계를 선형으로 설명한 것이다.
2. 다항 회귀분석: 단순 회귀분석으로서는 분석되지 않는 Data를 단순 회귀식의 차원을 높여가며 회귀식을 설립하는 방법 즉, 회귀분석 5가지 조건중 선형성을 해결하기 위한 방법 중 하나이다.
3. 다중회귀 분석: 독립변수가 복수인 경우 사용한다. 많은 독립변수중 어떠한 것을 선택할 지 정하는 것이 중요하다.
4. 로지스틱 회귀 분석: 연속형인 종속변수를 사용하기 위해서 사용
   회귀분석 - 독립변수: 연속형, 종속변수: 연속형.
   
   로지스틱 회귀분석 - 독립변수: 연속형, 종속변수: 범주형.
   

단순 회귀 분석 기초

#단순 회귀분석
df<-data.frame(workhour=1:7,totalpay=seq(10000,70000,by=10000))
df
plot(totalpay~workhour,data=df)
grid()
model<-lm(totalpay~workhour,data=df)
model
abline(model,col="red",lwd=2)
#y = 1.0e+04*x -5.5e-12

출력결과-Model 내용

출력결과-Model 시각화

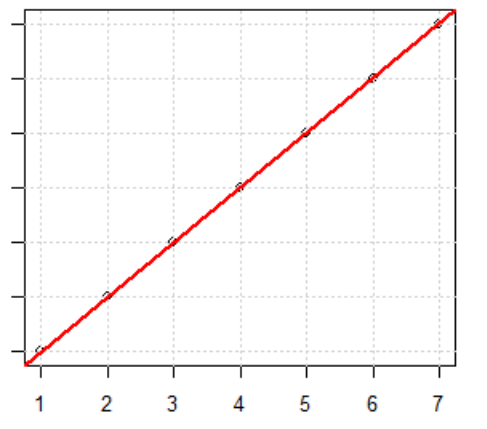
단순 회귀 분석

#단순 회귀분석
#단순회귀 분석
head(women)
plot(weight~weight,data=women)
#상관관계 분석
cor.test(women$weight,women$height)
#회귀 모델 만들기
model<-lm(weight~height,data=women)
model
abline(model,col='blue')
summary(model)
par(mfrow=c(2,2))
plot(model)

출력결과-Model 내용

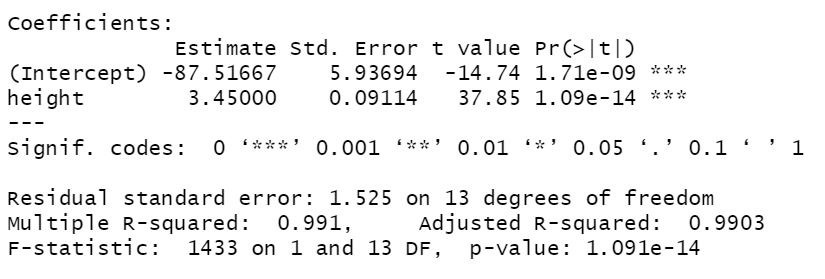
P-value: 회귀모델이 유의한지 안한지 판단 EX) p-value(1.09e-14)<0.05 => 회귀모델은 유의하다.
R-squared: 설명력 EX)R-squared=0.991(99.1%)로 충분한 설명력을 가지고 있다.
출력결과-Model 사진

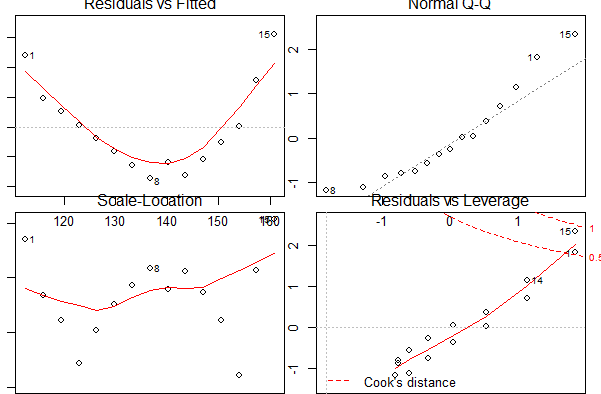
1. 정규성: 정규성 가정을 만족한다면 이 그래프의 점들은 45도 각도의 직선 위에 있어야 한다.
2. 독립성: 반응변수는 서로 독립적이여야 한다.
3. 선형성: 종속변수와 독립변수가 선형관계에 있다면 잔차와 예측치 사이에 어떤 체계적인 관계가 있으면 안 된다.
4. 등분산성: 분산인 일정하다는 가정을 만족한다면 왼쪽 아래의 그림에서 수평선 주위의 random band 형태로 나타나야 한다.
   참초: Keon-Woong Moon 블로그
   

다항 회귀 분석

#다항 회귀 분석
model2<-lm(weight~height+I(height^2),data=women)
summary(model2)
plot(model2)
par(mfrow=c(2,2))

출력결과-Model 내용

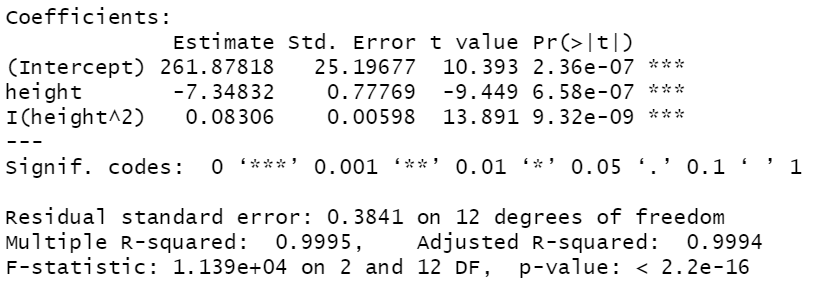
height 독립변수를 2차까지 늘렸다
p-value: 1.09e-14 => 2.2e-16
R-squared: 0.991(99.1%) => 0.9995
p-value 감소, R-squared증가 => Model 능력 향상
출력결과-Model 사진

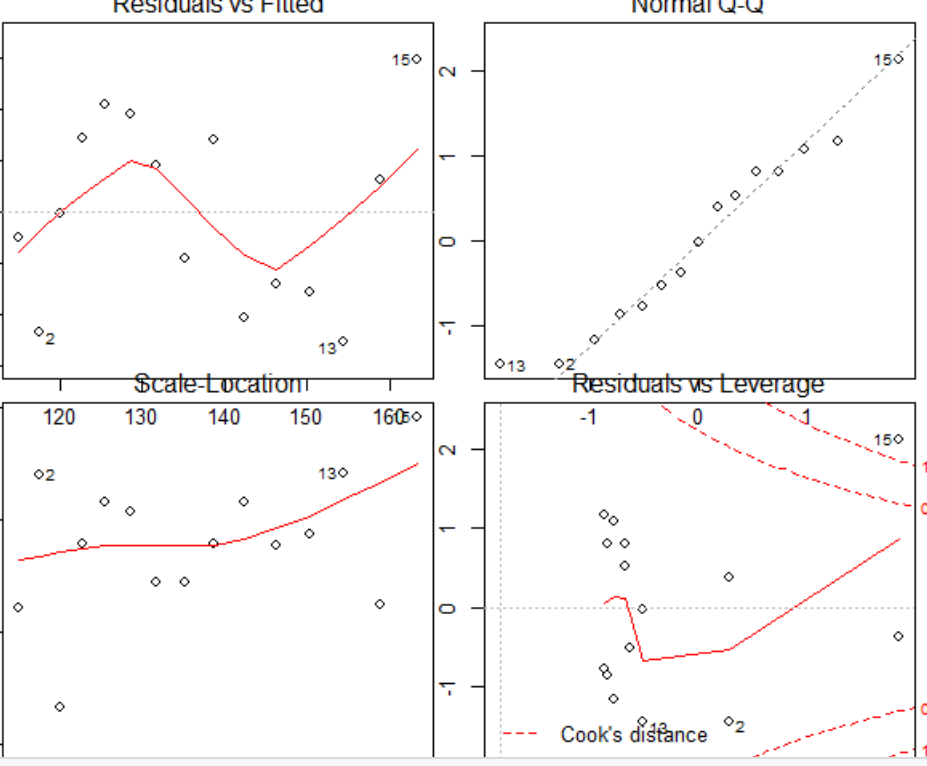
3사분면인 선형성 관련 그래프가 많이 달라진 것을 알 수 있다.

다중 회귀 분석

다중회귀 분석에서는 독립변수의 개수가 많으므로 어떠한 변수를 선택하는 것에 따라 Model의 성능을 좌우하게 된다.
AIC 통계량: 여러 통계모델들의 성능을 서로 비교할 수 있게 해준다. 예를들어, 개인의 낮은 사회경제학적 지위에 기여하는 변수가 어떤 것인지, 그리고 이 변수들이 어떻게 그 지위에 영향을 주는 지 알 수 있게 해준다.

1. Forward: 변수들을 하나씩 증가시키면서 Model 성능 평가
2. Backward: 모든 변수를 참여시키고 기여도가 낮은 것부터 제거하는 방법(변수의 개수가 너무 많으면 문제가 발생할 수 있다. 대부분 20개 미만을 사용한다.)
   참조: Kyoyoung Chu 블로그

#다중 회귀 분석
#Data 불러오기
install.packages("car")
library(car)

head(iris)
dim(iris)
cor(iris[,-5])
#Data Train Data와 Test Data 분류
sam_tt<-sample(1:nrow(iris),nrow(iris)*0.7,replace = F)
train<-iris[sam_tt,]
test<-iris[sam_tt,]
dim(train)
dim(test)
#다중공선성 확인
#10 이상의 값은 제거한다.
model<-lm(Sepal.Length~Sepal.Width+Petal.Width+Petal.Length,data=train)
vif(model)
#Model 만들기
model<-lm(Sepal.Length~Sepal.Width+Petal.Width,data=train)
vif(model)
#Model 확인 및 시각화
res<-residuals(model)
shapiro.test(res)
par(mfrow=c(2,2))
plot(model)
#잔차의 독립성 확인
install.packages("lmtest")
library(lmtest)
dwtest(model)
summary(model)

출력결과-다중공선성 학인

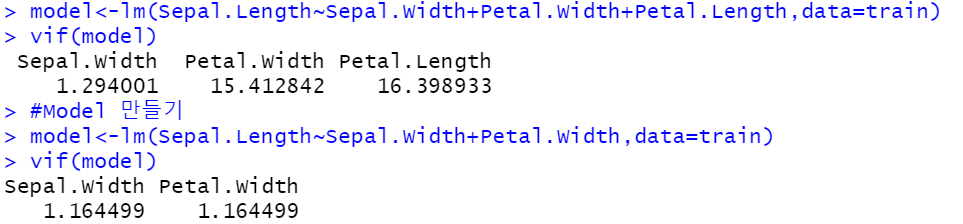
출력결과-Model 사진

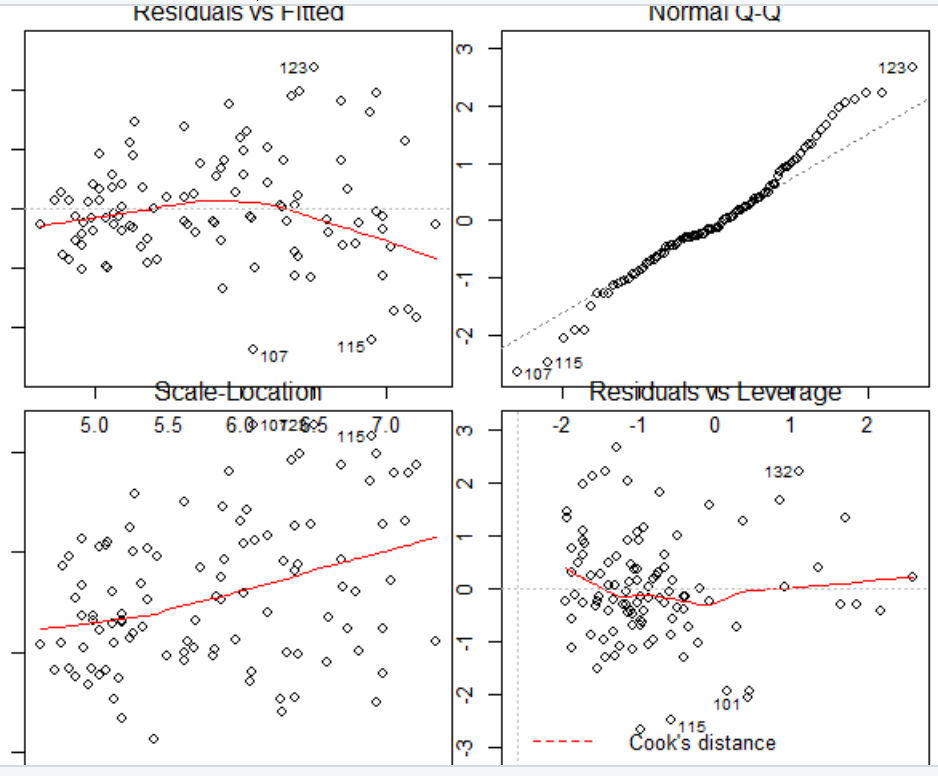
출력결과-잔차의 독립성 학인

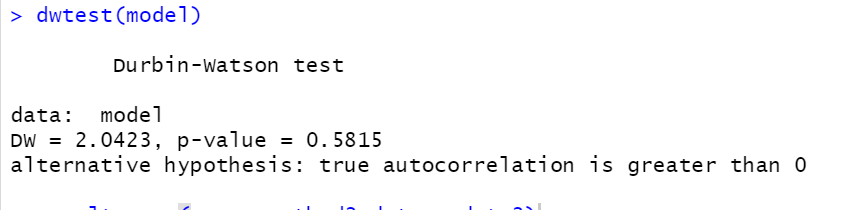
출력결과-Model 확인

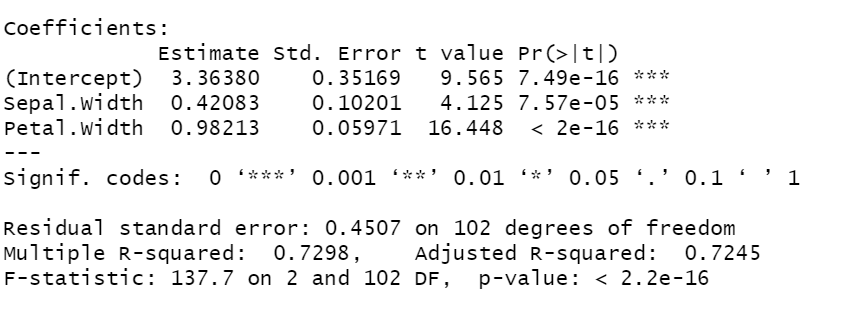
로지스틱 회귀분석

로지스틱 회귀는 이항형 또는 다향형이 될 수 있다. 종속변수의 결과가 2개의 종류라면 이항형, 그 이상이라면 다항형이다.
이항형: 시그모이드, 다항형: 소프트맥스
ROC curve (Receiver Operating Characteristic curve) : FPR과 TPR을 각각 x,y축으로 놓은 그래프
TPR : True Positive Rate (=민감도, true accept rate) 1인 케이스에 대해 1로 예측한 비율.(암환자를 진찰해서 암이라고 진단 함)
FPR : False Positive Rate (=1-특이도, false accept rate) 0인 케이스에 대해 1로 잘못 예측한 비율.(암환자가 아닌데 암이라고 진단 함)
민감도 : 1인 케이스에 대해 1이라고 예측한 것.
특이도 : 0인 케이스에 대해 0이라고 예측한 것.
AUC = AUROC (the Area Under a ROC Curve) : ROC 커브의 밑면적을 구한 값이 바로 AUC. 이 값이 1에 가까울수록 성능이 좋다.

AUC 해석 : 1로 예측하는 기준을 쉽게 잡으면 민감도는 높아진다. 그대신 모든 경우를 1이라고 하므로 따라서 특이도가 낮아진다. 그러므로 이 두 값이 둘다 1에 가까워야 의미가 있다. 그래서 ROC커브를 그릴때 특이도를 1-특이도를 X축에 놓고, Y축에 민감도를 놓는다. 그러면 x=0일때 y가 1이면 가장 최고의 성능이고, 점점 우측 아래로 갈수록, 즉 특이도가 감소하는 속도에비해 얼마나 빠르게 민감도가 증가하는지를 나타냄.
출처: newsight 블로그

#로지스틱 회귀 분석
#데이터 읽어오고 확인하기
weather<-read.csv("C:/git/R/Data/weather.csv",stringsAsFactors = F)
head(weather)
names(weather)

#이항 로지스틱 회귀에서 Sigmoid를 사용하기 위하여 1,0으로 변환
weather_df<-weather[,c(-1,-6,-8,-14)]
weather_df$RainTomorrow[weather_df$RainTomorrow=='Yes']<-1 #더미변수화 시켰다.
weather_df$RainTomorrow[weather_df$RainTomorrow=='No']<-0
weather_df$RainTomorrow<-as.numeric(weather_df$RainTomorrow)
head(weather_df)

#TrainData와 TestData 분리
idx<-sample(1:nrow(weather_df),nrow(weather_df)*0.7)
train<-weather_df[idx,]
test<-weather_df[-idx,]
dim(train)
dim(test)

#Model 만들기
weather_model<-glm(RainTomorrow~.,data=train,family = "binomial")
summary(weather_model)

#예측치 얻기
pred<-predict(weather_model,newdata = test,type="response")
head(pred)

#정확도 측정
result_pred<-ifelse(pred>=0.5,1,0)
table(result_pred)
table(result_pred,test$RainTomorrow)
(89+6)/nrow(test)#정확도  0.8636...

#정확도 측정 - ROC
install.packages("ROCR")
library(ROCR)
pr<-ROCR::prediction(pred,test$RainTomorrow)
prf<-ROCR::performance(pr,measure="tpr",x.measure = "fpr")
plot(prf)

#ROC 면적 - AUC 구하기
auc<-performance(pr,measure="auc")
auc<-auc@y.values[[1]]
auc

출력결과 - 변수 P-value

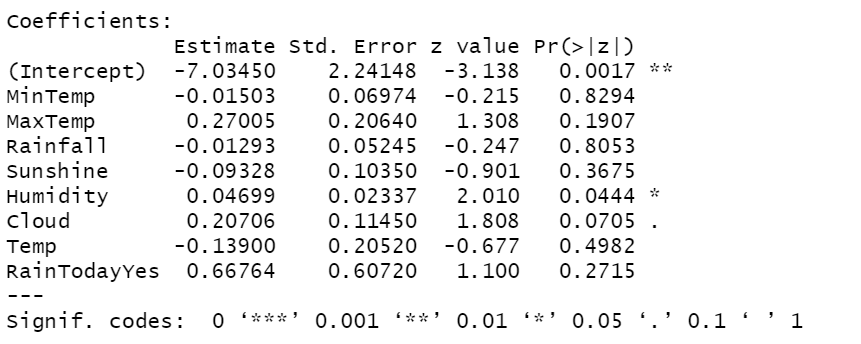
P-value 낮은 변수 값을 선택한다.

출력결과 - Cross Table로 정확도 확인

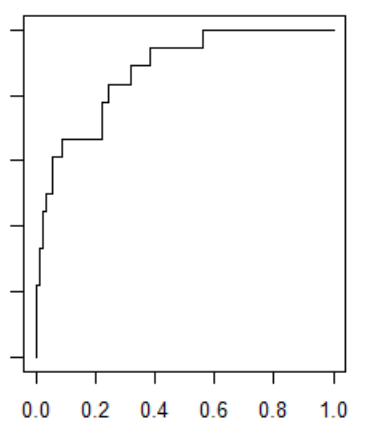
출력결과 - ROC Curve

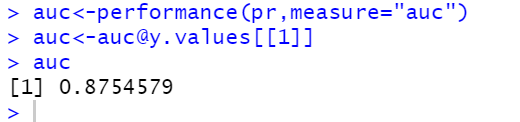
출력결과 - AUC를 통한 정확도 확인

---

참조: 원본코드
코드에 문제가 있거나 궁금한 점이 있으면 wjddyd66@naver.com으로 Mail을 남겨주세요.