Statistics(7)-Student’s t-Distribution, Student’s F-Distribution

이번 POST는 한양대학교 수리통계학 수업 내용을 정리한 것 입니다.
문제나 자세한 내용은 mykepzzang 블로그를 참조하였습니다.

9. t-분포, f분포

(1) t-분포(Student’s t-Distribution)

먼저 t-분포에 대해 알기전에 카이제곱 분포에서 식을 유도한 다음 진행하여야 한다.
유도해야 하는 식은 다음과 같다.
모집단의 정규분포인 \(N(\mu,\sigma^2)\)으로부터
크기가 n인 랜덤표본 \(X_1, X_2, ..., X_n\)을 추출하고,
이때 표본분산을 \(S^2\)라고 하면

$$\frac{(n-1)S^2}{\sigma^2} = \sum_{i=1}^{n} \frac{(X_i-\bar{X})^2}{\sigma^2}$$

은 자유도가 (n-1)인 카이제곱 분포를 따른다.
위의 식을 유도하면 다음과 같다.

$$s^2 = \sum_{i=1}^{n} \frac{(X_i-\bar{X})^2}{n-1}, \bar{X} = \frac{1}{n} \sum_{i=1}^{n} X_i$$

$$\frac{(n-1)S^2}{\sigma^2} = \sum_{i=1}^{n} \frac{(X_i-\bar{X})^2}{\sigma^2}$$

위의 식에서 \(\sum_{i=1}^{n} (X_i-\bar{X})^2\)만 따로 생각하면 다음과 같다.

$$\sum_{i=1}^{n} (X_i-\mu)^2 = \sum_{i=1}^{n} (X_i-\bar{X})^2 + n(\bar{X} = \mu)$$

위의 수식 유도가 이해되지 않으면 6. Sampling분포에 (3) 표본분산(Sample variance)의 분포 의 수식을 참조하자.

$$\therefore \sum_{i=1}^{n} \frac{(X_i-\mu)^2}{\sigma^2} = \frac{(n-1)S^2}{\sigma^2} + (\frac{\bar{X}-\mu}{\frac{\sigma}{\sqrt{n}}})^2$$

$$\rightarrow \frac{(n-1)S^2}{\sigma^2} = \sum_{i=1}^{n} \frac{(X_i-\mu)^2}{\sigma^2} - (\frac{\bar{X}-\mu}{\frac{\sigma}{\sqrt{n}}})^2$$

$$= \chi_{n}^2 - \chi_{1}^2 = \chi_{n-1}^2$$

$$\because \sum_{i=1}^{n} \frac{(X_i-\mu)^2}{\sigma^2} = \sum_{i=1}^{n} N \text{~} (\mu,\sigma^2) \text{, Z 정규화}$$

$$\because (\frac{\bar{X}-\mu}{\frac{\sigma}{\sqrt{n}}})^2 = \sum_{i=1}^{1} N \text{~} (\mu,\sigma^2) \text{, Z 정규화, }E(\bar{X}) = \mu, V(\bar{X}) = \frac{\sigma^2}{n}$$

위의 식을 활용하여 t분포에 대해서 알아본다.

t-분포는 표본평균을 이용해 정규분포의 평균을 해석할 때 많이 사용한다. 그리고 R Category, DataAnalysis Category에서 살펴보았듯이 가설검정에서 많이 사용되는 분포이다.
t분포에 대한 정의는 아래와 같이 정의된다.

확률변수 Z는 표준정규분포를 따르고, V는 자유도가 v인 카이제곱분포를 따를 때, 서로 독립인 Z와 V에 대해 새로운 확률변수 T는 다음과 같다.

$$T = \frac{Z}{\sqrt{\frac{V}{v}}}$$

그리고 확률변수 T는 자유도가 v인 t-분포를 따른다. 위의 t-분포의 정의에서 각각의 변수를 위에서 정리한 식에 Mapping을 하면 다음과 같다.

• \(v: n-1\)
• \(V: \frac{(n-1)S^2}{\sigma^2}\)
• \(Z: N \text{~} (0,1)\)

위의 식에서 중요한 것은 Z를 알아내기 위하여 Z정규화를 통하여 표본정규분포로 바꾸어야 된다는 것 이다.
\(Z = \frac{\bar{X}-\mu}{\frac{\sigma}{\sqrt{n}}}\)로서 전체표본의 모수인 \(\mu, \sigma\)를 알아야 한다는 단점이 생기게 된다.

따라서 위의 식을 다음과 같이 바꾸어서 많이 사용한다.

$$T = (\bar{X}-\mu)\frac{\sqrt{n}}{S}$$

위의 식은 자유도가 (n-1)인 t-분포를 따른다.
위의 식을 유도하면 다음과 같다.

$$T = \frac{Z}{\sqrt{\frac{V}{v}}} = \frac{1}{\sqrt{\frac{V}{v}}} \frac{\sqrt{n}}{\sigma}(\bar{X}-\mu)$$

$$= \sqrt{n}(\bar{X}-\mu)\frac{1}{\sqrt{\frac{V\sigma^2}{v}}} = \sqrt{n}(\bar{X}-\mu)\frac{1}{\sqrt{S^2}} = (\bar{X}-\mu)\frac{\sqrt{n}}{S}$$

위의 식으로 인하여 모수중 하나인 \(\sigma\)를 몰라도 되고 t-분포의 목적인 표본평균을 이용해 정규분포의 평균을 해석할 때 사용될 수 있다.

t-분포가 다음과 같을 때 t-분포의 확률밀도함수 f(t)는 다음과 같다.

$$f(t) = \frac{\gamma(\frac{v+1}{2})}{\gamma(\frac{v}{2})\sqrt{\pi v}}(1+\frac{t^2}{v})^{-\frac{v+1}{2}}\text{ , } -\infty < t < \infty$$

f(t)를 자유도 v를 가진 t-분포의 확률밀도 함수라고 한다. (\(\gamma\)는 감마함수)

이러한 t-분포는 정규분포와 같이 t-분포표를 활용하여 구하게 된다.

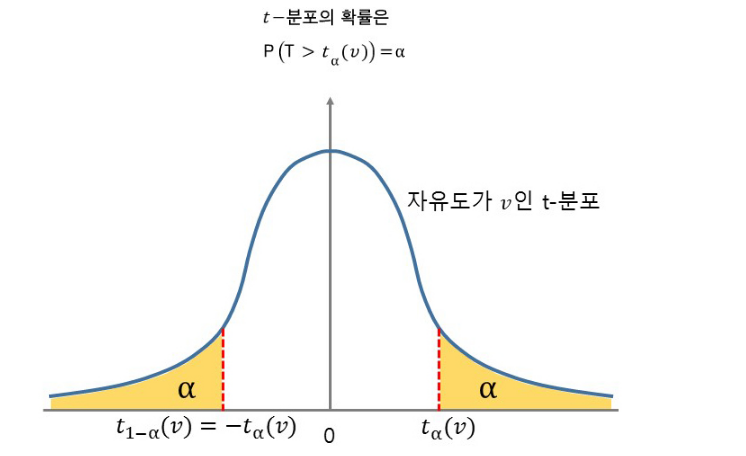
사진 출처: mykepzzang 블로그

또한 중요한 것은 t-분포 또한 중심극한 정리에 의해서 \(n \rightarrow \infty\)즉, 표본의 크기가 커지게 되면 정규분포가 된다. 따라서 표본의 크기가 일정크기(대부분 30 이하)일 경우 사용하게 된다.

평균: \(E(T) = 0, v > 1\)
분산: \(V(T) = \begin{cases} \frac{v}{v-2}, & v>2 \\ \ \infty & 1 < v \le 2 \end{cases}\)

ex) 확률변수 T는 자유도 19인 t-분포일 때, \(P(T \ge t) = 0.025\)를 만족하는 t를 구하시오.
실제 t-분포표를 확인하여 문제를 해결해보자.
다음 분포표는 다음과 같은 식일 때 보는 표이다.

$$P(T \ge t) = \alpha\text{ , } df: \text{자유도}$$

사진 출처: math100 블로그

따라서 문제와 Parameter를 Mapping해서 값을 찾아보면 다음과 같다.

• \(\alpha\): 0.025
• \(df\): 19

$$t_{\alpha}(df) = t_{0.025}(19) = 2.093$$

따라서 이전까지 배운 분포의 최종적인 관계를 표현하면 다음과 같이 표현할 수 있다.
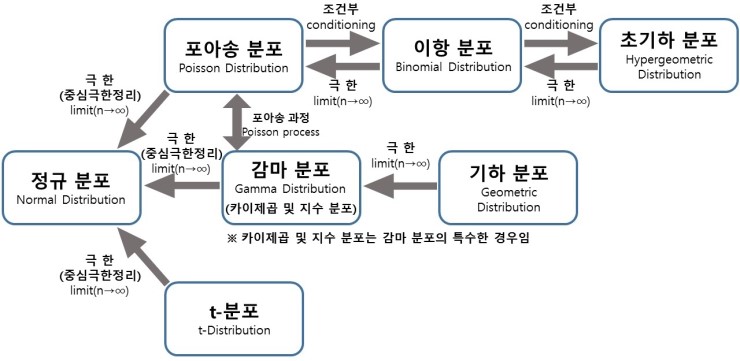
사진 출처: mykepzzang 블로그

(2) F분포(Sendocor’s F-Distribution)

F-분포는 정규분포를 이루는 모집단에서 독립적으로 추출한 표본들의 분산 비율이 나타내는 연속확률 분포 이다. 2개 이상의 표본평균들이 동일한 모평균을 가진 집단에서 추출되었는지 아니면 서로 다른 모집단에서 추출된 것인지를 판단하기 위하여 사용된다.

F-분포의 정의를 살펴보면 다음과 같다.
서로 독립인 두 확률면수 U와 V가 각각 자유도가 \(v_1, v_2\)인 카이제곱분포를 따를 때, 새로운 확률변수 F는 다음과 같다.

$$F=\frac{\frac{U}{v_1}}{\frac{V}{v_2}}$$

위의 F는 자유도가 \((v_1,v_2)\)인 F-분포를 따른다.

F-분포의 확률밀도함수는 다음과 같다.

$$ g(F) = \begin{cases} \frac{\sigma(\frac{v_1+v_2}{2})(\frac{v_1}{v_2})^{\frac{v_1}{2}}}{\sigma(\frac{v_1}{2})\sigma(\frac{v_2}{2})} \frac{f^{\frac{v_1}{2}-1}}{(1+\frac{v_1}{v_2}f)^{\frac{v_1+v_2}{2}}}, & f>0 \\ \ 0 & f \le 0 \end{cases} $$

F-분포 또한 t-분포와 같이 확률분포표를 참조하여서 값을 구하지, 위와 같은 확률밀도함수로서 값을 구하지 않는다.

F-분포의 확률(f-value)은 다음과 같다.

$$p[F \ge f_{\alpha}(v_1,v_2)] = \alpha$$

위의 확률영역을 그림으로 나타내면 다음과 같다.

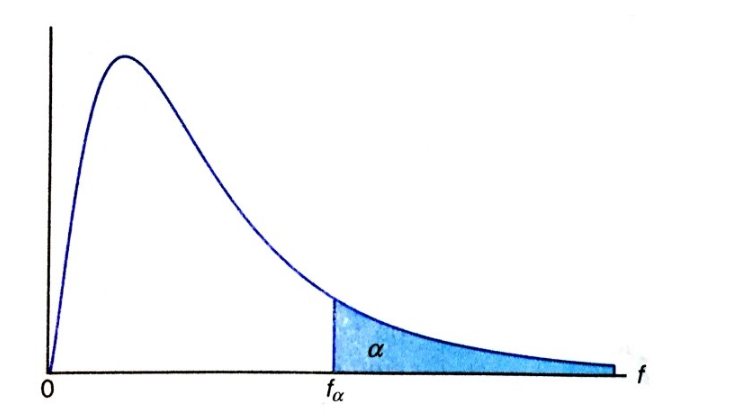
사진 출처: mykepzzang 블로그

F-분포 성질
F분포는 다음과 같은 성질을 따른다.
1) \(f_{1-\alpha}(v_1,v_2) = \frac{1}{f_{\alpha}(v_2,v_1)}\)
위의 식을 설명하면 확률변수 F가 자유도 \((v_1,v_2)\)인 F-분포를 따를 때, \(\frac{1}{F}\)는 자유도 \((v_2,v_1)\)인 F-분포를 따른다.

2) \(F=\frac{\frac{U}{v_1}}{\frac{V}{v_2}}\)일 경우 자유도가 \((n_1-1,n_2-1)\)인 F-분포를 따른다.
위의 성질을 사용하기 위하여 다음과 같이 정의해야 하는 조건들이 존재한다.
모분산이 각각 \(\sigma_1^2,\sigma_2^2\)인 정규모집단에서 서로 독립적으로 추출된 크기 \(n_1,n_2\)인 표본의 분산을 각각 \(S_1^2, S_2^2\)일 때
\(F=\frac{\frac{U}{v_1}}{\frac{V}{v_2}}\)은 자유도가 \((n_1-1,n_2-1)\)인 F-분포를 따른다.
위의 식에서 각각의 \(U,V\)는 다음과 같이 정의 될 수 있다.

$$U=\frac{(n_1-1)S_1^2}{\sigma_1^2} \rightarrow \chi_{n_1-1}^2$$

$$V=\frac{(n_2-1)S_2^2}{\sigma_2^2} \rightarrow \chi_{n_2-1}^2$$

$$\therefore F=\frac{\frac{U}{v_1}}{\frac{V}{v_2}} \rightarrow F(n_1-1,n_2-1) \because \text{F-분포의 정의로 인하여}$$

---

참조: 한양대학교 수리통계학 수업
참조: mykepzzang 블로그
코드에 문제가 있거나 궁금한 점이 있으면 wjddyd66@naver.com으로 Mail을 남겨주세요.