TensorFlow-Linear Regression

Linear Regression

‘선형적이다’ 라는 표현은 영어로 linear 하다 라고 말한다. linear란 line(선)의 형용사 형태입니다. 이 말에서 유추할 수 있듯이, 선형적이란 것은 어떤 성질이 변하는데 그 변수가 1차원적이다, 즉 어떤 신호에 기울기만 곱한 형태와 같다.

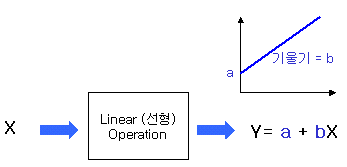
그림출처:www.rfdh.com
간단한 수식으로는 y= bx + a로서 표현할 수 있다.
여기서 우리가 중점적으로 봐야할 것은 weight: b, bias: a의 상수 2개이다.
이 상수 2개를 찾아낼 수 있으면 우리는 앞으로 Input이 들어올 경우 Output을 구할 수 있다.
회귀분석 자세한 내용

Linear Regression 예시

아래 표와 같은 DataSet이 있다고 가정하자.

집넓이	집값(만원)
10	3000
15	4000
16	12000
...	...
60	30000

위의 집 넓이를 X, 집값을 Y라 하였을때 다음과 같은 식을 얻을 수 있다.

\(y= w_1 X + b\)
위의 식은 아래와 같은 그래프로서 표현할 수 있다.

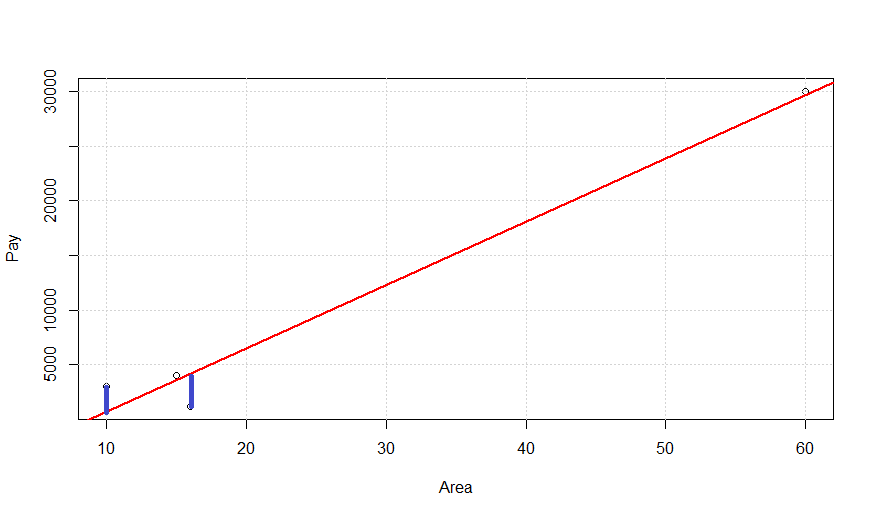
실제값과 예측값의 차이는 파란색선의 길이의 합이다.
실제값과 예측값의 차이는 Cost라고 불리게 되고 이러한 Cost에 대한 식은 아래 식으로 나타낼 수 있다.

\(f_c(x)=\sum_{i=0}^n (y_i-\hat{y_i})^2\)
Loss Function은 아래와 같은 그림으로 나타낼 수 있다.

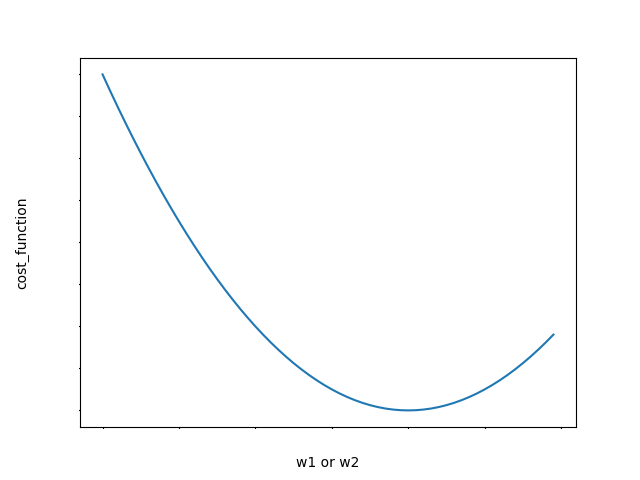
Cost가 0이 될 확률을 매우 낮지만 0에 가까울 때(미분했을때의 기울기가 0인 점)의 값을 구하는 것이 Cost를 최소로 할 수 있다.
간단하게 구할 수 있다고 생각하지만 Weight가 많아지게 되면 수식이 복잡하게 되므로 Gradient Decent를 사용하게 된다.
GradientDescent의 자세한 내용

Linear Regression 실제 구현

Linear Regression을 실제로 구현하기 전에 구현하기 위하여 사용된 기법을 먼저 정리하였다.
Linear Regression 사용 기법

Model	y= 2 x
Loss Function	MSE
Optimazation	GradientDescent

Linear Regression 실제 구현
변수(Variable)와 플레이스홀더(placeholder) 를 이용하여 선형회귀 모델의 그래프 구조 (Wx + b) 선언

• W: 가중치
• b: 바이어스
• x: 입력값
• y: 출력값

W = tf.Variable(tf.random_normal(shape=[1]))
b = tf.Variable(tf.random_normal(shape=[1]))
x = tf.placeholder(tf.float32)
linear_model = W*x + b
y = tf.placeholder(tf.float32)

Loss Function: MSE 선언
텐서보드를 위한 요약정보(scalar)선언

loss = tf.reduce_mean(tf.square(linear_model-y))
#텐서 보드를 위한 요약정보 scalar
tf.summary.scalar('loss',loss)

텐서 보드를 위한 Merge 및 File경로 설정

merged = tf.summary.merge_all()
tensorboard_writer = tf.summary.FileWriter('./tensorboard_log',sess.graph)

Optimier 선언: GradientDescent

optimizer = tf.train.GradientDescentOptimizer(0.01)
train_step = optimizer.minimize(loss)

실제 Data

X_train = [1, 2, 3, 4]
Y_train = [2, 4, 6, 8]

Session 실행
Step마다 merged 연산을 실행하고 저장

optimizer = tf.train.GradientDescentOptimizer(0.01)
train_step = optimizer.minimize(loss)

X_train = [1, 2, 3, 4]
Y_train = [2, 4, 6, 8]

sess = tf.Session()
sess.run(tf.global_variables_initializer())

for i in range(1000):
    sess.run(train_step,feed_dict={x:X_train, y:Y_train})
    
    #매 Step마다 요약정보 값들을 저장하여 지정된 경로에 저장
    summary = sess.run(merged,feed_dict={x:X_train, y:Y_train})
    tensorboard_writer.add_summary(summary,i)

Model Test 및 Session 닫기

X_test = [3.5, 5, 5.5, 6]
print(sess.run(linear_model,feed_dict={x:X_test}))

sess.close()

Linear Regression 결과

실제 값	예측 값	차이
7	7.0019174	0.0019174
10	10.007053	0.007053
11	11.008765	0.008765
12	12.010476	0.010476

TensorBoard Loss 결과

---

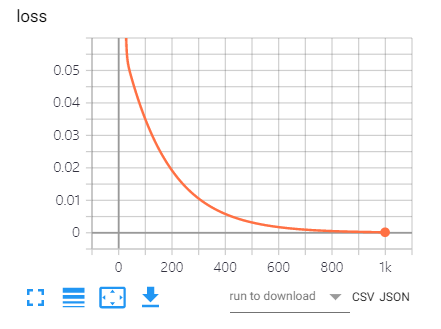
참조: 원본코드
참조: Chanwoo Timothy Lee Youtube
참조: honeytip91 블로그
문제가 있거나 궁금한 점이 있으면 wjddyd66@naver.com으로 Mail을 남겨주세요.