Paper12. DeepCCA
Deep Generalized Canonical Correlation Analysis
출처: Deep Generalized Canonical Correlation Analysis
코드: DGCCA Pytorch Code
PLS의 Data를 Label을 사용하지 않고, Modality만 사용하였을 경우 CCA(Canonical Correlation Analysis) 라고 정의한다.
DCCA(Deep Generalizaed Canonical Correlation Analysis)는 이러한 CCA에서 Modality가 여러개라는 Generalized와 Deep Learning Model을 추가하여 Non-Linearity를 추가한 방법이다.
Notation
- \(X_j \in R^{d_j \times N}\): Input
- \(J\): Num of modality
- \(N\): Num of sample
- \(o_j\): Hidden layer output dimension
- \(f\): DNN
- \(r\): Dimension reduction
Object Function
$$\min_{U_j \in R^{o_j \times r}, G \in R^{r \times N}} \sum_{j=1}^J \|G-U_j^T f_j(X_j)\|_F^2$$
Gradient Derivation For Weight Matrix
Probelm: How to define G -> Find by using eigenvector(SVD)
1) \(C_{jj} = f(X_j)f(X_j)^T \in R^{o_j \times o_j}\): Symmetric Matrix
2) \(P_j = f(X_j)^T C_{jj}^{-1} f(X_j) \in R^{N \times N}\): Symmetric & Idemcompotent Matrix
\(P_jP_j = f(X_j)^T C_{jj}^{-1} f(X_j)f(X_j)^T C_{jj}^{-1} f(X_j) = f(X_j)^T C_{jj}^{-1} f(X_j) = P_j\): Idecomponent Matrix
\((\because C_{jj}^{-1} f(X_j)f(X_j)^T = (f(X_j)^T)^{-1}f(X_j)^{-1}f(X_j)f(X_j)^T) = I)\)
\(P_j P_j^T = (f(X_j)^T C_{jj}^{-1} f(X_j)) (f(X_j)^T C_{jj}^{-1} f(X_j))^T\)
\(= f(X_j)^T C_{jj}^{-1} f(X_j) f(X_j)^T (C_{jj}^{-1})^T f(X_j) = f(X_j)^T C_{jj}^{-1} C_{jj} (C_{jj}^{-1})^T f(X_j)\)
\(= f(X_j)^T C_{jj}^{-1} f(X_j) (\because C_{jj} = \text{Symmetric Matrix}) = P_j\): Symmetric Matrix
3) \(M = \sum_{j=1}^J P_j\): Symmetric Matrix (\(\because \text{Sum of Symmetric Matrix}\))
4) \(G \in R^{N \times r} \rightarrow \text{Top r eigenvector of M} \rightarrow \text{Top r orthogonal eigenvector of M}\): 모든 \(f(X_j)\)를 대표할 수 있는 Low-Rank Matrix , SVD를 활용하여 Eigenvector를 찾는다.
if \(A \rightarrow \text{Symmetric Matrix}\)
\(\lambda_1 u_2^{T}u_1 = u_2^{T}(Au_1) = (u_2^{T}A)u_1 = (A^{T}u_2)^{T}u_1 = (Au_2)^{T}u_1 = \lambda_2u_2^{T}u_1\)
\((\lambda_1 - \lambda_2)u_2^{T}u_1 = 0\)
\(\lambda_1 , \lambda_2 \neq 0 이므로 u_2^{T}u_1 = 0 \rightarrow u_2^{T}u_1 = 0 이므로 서로 직교(orthogonal)한다.\)
5) Object Function에 \(G, C_{jj}\)를 대입하면 \(U_j = C_{jj}^{-1} f(X_j)G^T\)으로서 정의될 수 있다.
\(U_j^T f_j(X_j) = G f(X_j)^T (C_{jj}^{-1})^T f(X_j) = G\)
\(\because (C_{jj}^{-1})^T = ((f(X_j)^T)^{-1} (f(X_j))^{-1})^T = (f(X_j)^T)^{-1} (f(X_j))^{-1}\)
6) 1~5를 활용하여 Object Function을 다시 정의하면 다음과 같다.
\(\sum_{j=1}^J \|G-U_j^T f_j(X_j)\|_F^2\)
\(= J\|G\|^2_F - \sum_{j=1}^{J}\|U_j^T f_j(X_j)\|_F^2\)
\(\approx \tau J - \sum_{j=1}^{J} \text{Tr}(U_j f_j(X_j) U_j f_j(X_j)^T)\)
\(= \tau J - \sum_{j=1}^J \text{Tr} (G f(X_j)^T (C_{jj}^{-1})^T f_j(X_j)G^T)\)
\(= \tau J - \sum_{j=1}^J \text{Tr} (G f(X_j)^T C_{jj}^{-1} f_j(X_j)G^T) (\because C_{jj} = \text{Symmetric Matrix})\)
\(= \tau J - \sum_{j=1}^J \text{Tr} (G P_j G^T)\)
\(= \tau J - \text{Tr}(GMG^T)\)
7) 6번의 식을 정리하면 다음과 같다.
\(\min_{U_j \in R^{o_j \times r}, G \in R^{r \times N}} \sum_{j=1}^J \|G-U_j^T f_j(X_j)\|_F^2 \approx \max \text{Tr}(GMG^T)\)
\(G\)는 top r orthogonal eigenvector of M이므로 \(GG^{T} \approx M\)이다. 따라서 최종적인 식은 다음과 같이 정리될 수 있다.
\(\text{Loss Function} = \max \sum_{i=1}^{r} \lambda_i (M)\text{, Sum of Eigen Value}\)
결국, G를 모든 \(f(X_j)\)를 대표할 수 있는 Low-Rank Matrix로서 나타내기 위하여 top r orthogonal eigenvector of M선택하는 것이 자동적으로 Loss Function을 최소화 하는 방법이고, 이로 인하여 weight matrix는 자동적으로 구할 수 있다. Hyperparameter인 r을 설정하는 것만 신경써주면 된다.
Gradient Derivation For DNN
Feature Extractor에서 나오는 Output인 \(f_j(X_j)\)에 Gradient를 전달할 수 있었야지 \(f\)의 parameter를 학습할 수 있다.
따라서, 해당 논문에서는 다음과 같이 정의하여 Gradient를 \(f\)에 전달하였다.
$$L = \min \sum_{j=1}^J \|G-U_j^T f_j(X_j)\|_F^2$$
$$= \min \text{Tr}((G-U_j^T f_j(X_j))^T(G-U_j^T f_j(X_j)))$$
$$= \min \text{Tr}(GG^T)-2\text{Tr}(U_j Gf_j(X_j)^T)+\text{Tr}(U_jU_j^T f_j(X_j)f_j(X_j)^T)$$
$$\therefore \frac{\partial L}{\partial f_j(X_j)} = 2U_jG-2U_ju_j^T f_j(X_j)$$
위의 식으로 인하여 Hidden Layer Output에 Gradient를 전달하면, Backpropagation으로서 Gradient를 전달 가능하다.
Deep GCCA Code
Import Library
1
2
3
4
import torch
import torch.nn as nn
import pandas as pd
from copy import deepcopy as copy
GCCA Loss
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
def GCCA_loss(H_list):
r = 1e-4
eps = 1e-8
# H1, H2, H3 = H1.t(), H2.t(), H3.t()
# print(f'H1 shape ( N X feature) : {H1.shape}')
# assert torch.isnan(H1).sum().item() == 0
# assert torch.isnan(H2).sum().item() == 0
# assert torch.isnan(H3).sum().item() == 0
# o1 = H1.size(0) # N
# o2 = H2.size(0)
top_k = 10
AT_list = []
for H in H_list:
assert torch.isnan(H).sum().item() == 0
o_shape = H.size(0) # N
m = H.size(1) # out_dim
# H1bar = H1 - H1.mean(dim=1).repeat(m, 1).view(-1, m)
Hbar = H - H.mean(dim=1).repeat(m, 1).view(-1, m)
assert torch.isnan(Hbar).sum().item() == 0
A, S, B = Hbar.svd(some=True, compute_uv=True)
A = A[:, :top_k]
assert torch.isnan(A).sum().item() == 0
S_thin = S[:top_k]
S2_inv = 1. / (torch.mul( S_thin, S_thin ) + eps)
assert torch.isnan(S2_inv).sum().item() == 0
T2 = torch.mul( torch.mul( S_thin, S2_inv ), S_thin )
assert torch.isnan(T2).sum().item() == 0
T2 = torch.where(T2>eps, T2, (torch.ones(T2.shape)*eps).to(H.device).double())
T = torch.diag(torch.sqrt(T2))
assert torch.isnan(T).sum().item() == 0
T_unnorm = torch.diag( S_thin + eps )
assert torch.isnan(T_unnorm).sum().item() == 0
AT = torch.mm(A, T)
AT_list.append(AT)
M_tilde = torch.cat(AT_list, dim=1)
# print(f'M_tilde shape : {M_tilde.shape}')
assert torch.isnan(M_tilde).sum().item() == 0
Q, R = M_tilde.qr()
assert torch.isnan(R).sum().item() == 0
assert torch.isnan(Q).sum().item() == 0
U, lbda, _ = R.svd(some=False, compute_uv=True)
assert torch.isnan(U).sum().item() == 0
assert torch.isnan(lbda).sum().item() == 0
G = Q.mm(U[:,:top_k])
assert torch.isnan(G).sum().item() == 0
U = [] # Mapping from views to latent space
# Get mapping to shared space
views = H_list
F = [H.shape[0] for H in H_list] # features per view
for idx, (f, view) in enumerate(zip(F, views)):
_, R = torch.qr(view)
Cjj_inv = torch.inverse( (R.T.mm(R) + eps * torch.eye( view.shape[1], device=view.device)) )
assert torch.isnan(Cjj_inv).sum().item() == 0
pinv = Cjj_inv.mm( view.T)
U.append(pinv.mm( G ))
U1, U2 = U[0], U[1]
_, S, _ = M_tilde.svd(some=True)
assert torch.isnan(S).sum().item() == 0
use_all_singular_values = False
if not use_all_singular_values:
S = S.topk(top_k)[0]
corr = torch.sum(S )
assert torch.isnan(corr).item() == 0
# loss = 14.1421-corr
loss = - corr
return loss
Define Model - DNN & DeepGCCA
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
class MlpNet(nn.Module):
def __init__(self, layer_sizes, input_size):
super(MlpNet, self).__init__()
layers = []
layer_sizes = [input_size] + layer_sizes
for l_id in range(len(layer_sizes) - 1):
if l_id == len(layer_sizes) - 2:
layers.append(nn.Sequential(
nn.Linear(layer_sizes[l_id], layer_sizes[l_id + 1]),
nn.Sigmoid(),
nn.BatchNorm1d(num_features=layer_sizes[l_id + 1], affine=False),
))
else:
layers.append(nn.Sequential(
nn.Linear(layer_sizes[l_id], layer_sizes[l_id + 1]),
nn.ReLU(),
# nn.BatchNorm1d(num_features=layer_sizes[l_id + 1], affine=True),
))
self.layers = nn.ModuleList(layers)
def forward(self, x):
for layer in self.layers:
x = layer(x)
return x
class DeepGCCA(nn.Module):
def __init__(self, layer_sizes1, layer_sizes2, input_size1, input_size2, outdim_size, use_all_singular_values, device=torch.device('cpu')):
super(DeepGCCA, self).__init__()
self.model1 = MlpNet(layer_sizes1, input_size1).double()
self.model2 = MlpNet(layer_sizes2, input_size2).double()
self.model3 = MlpNet(layer_sizes2, input_size2).double()
def forward(self, x1, x2, x3):
"""
x1, x2 are the vectors needs to be make correlated
dim=[batch_size, feats]
"""
# feature * batch_size
output1 = self.model1(x1)
output2 = self.model2(x2)
output3 = self.model3(x3)
return output1, output2, output3
Hyperparameter Tuning
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
lr = 1e-2
device = 'cpu'
torch.manual_seed(1)
# size of the input for view 1 and view 2
input_shape1 = 100
input_shape2 = 100
input_shape3 = 100
X1 = torch.randn((100, input_shape1), requires_grad=True).double().to(device)
X2 = torch.randn((100, input_shape2), requires_grad=True).double().to(device)
X3 = torch.randn((100, input_shape2), requires_grad=True).double().to(device)
outdim_size = 20
# number of layers with nodes in each one
layer_sizes1 = [50, 30, outdim_size]
layer_sizes2 = [50, 30, outdim_size]
layer_sizes3 = [50, 30, outdim_size]
Model Train
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
model = DeepGCCA(layer_sizes1, layer_sizes2, input_shape1, input_shape2, outdim_size, False, device).double().to(device)
lr = 1e-2
optimizer = torch.optim.SGD(model.parameters(), lr=lr, momentum=0.9, weight_decay=0.5)
scheduler = torch.optim.lr_scheduler.StepLR(optimizer, step_size=100, gamma=0.1)
criterion = GCCA_loss
train_loss = []
model.train()
for epoch in range(400):
optimizer.zero_grad()
out1, out2, out3 = model(X1, X2, X3)
loss = criterion([out1, out2, out3])
# print(loss)
train_loss.append(copy(loss.data))
loss.backward()
optimizer.step()
scheduler.step()
Check Train Loss
1
2
loss_plt = pd.DataFrame(train_loss)
loss_plt.plot()
1
<matplotlib.axes._subplots.AxesSubplot at 0x7f44989928d0>
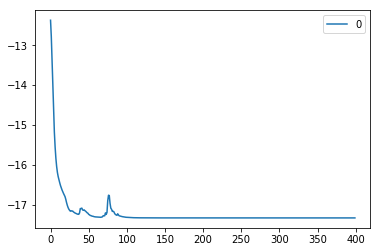
Check Loss
1
criterion([X1, X2, X3])
1
tensor(-12.3574, dtype=torch.float64, grad_fn=<NegBackward>)
1
2
3
print(criterion([X1, X1, X1]))
print(criterion([X2, X2, X2]))
print(criterion([X3, X3, X3]))
1
2
3
tensor(-17.3205, dtype=torch.float64, grad_fn=<NegBackward>)
tensor(-17.3205, dtype=torch.float64, grad_fn=<NegBackward>)
tensor(-17.3205, dtype=torch.float64, grad_fn=<NegBackward>)
참조: Deep Generalized Canonical Correlation Analysis
참조: DGCCA Pytorch Code
코드에 문제가 있거나 궁금한 점이 있으면 wjddyd66@naver.com으로 Mail을 남겨주세요.

Leave a comment