Paper18. Beyond triplet loss: a deep quadruplet network for person re-identification

Beyond triplet loss: a deep quadruplet network for person re-identification

출처: Beyond triplet loss: a deep quadruplet network for person re-identification
코드: sooooojinlee GitHub: Paper with Code에 적혀있는 Link입니다. 정확한 논문저자의 Github는 아닌 것 같습니다.

Abstract

Person re-identification (ReID) is an important task in wide area video surveillance which focuses on identifying people across different cameras. Recently, deep learning networks with a triplet loss become a common framework for person ReID. However, the triplet loss pays main attentions on obtaining correct orders on the training set. It still suffers from a weaker generalization capability from the training set to the testing set, thus resulting in inferior performance. In this paper, we design a quadruplet loss, which can lead to the model output with a larger inter-class variation and a smaller intra-class variation compared to the triplet loss. As a result, our model has a better generalization ability and can achieve a higher performance on the testing set. In particular, a quadruplet deep network using a margin-based online hard negative mining is proposed based on the quadruplet loss for the person ReID. In extensive experiments, the proposed network outperforms most of the state-of-the-art algorithms on representative datasets which clearly demonstrates the effectiveness of our proposed method.

해당 논문에서 Triplenet Loss를 사용하는 Model들의 공통적인 문제점은 Triplet Dataset에서 Training을 어떻게 하는지가 중요하다는 것 이다. 예를 들어, Dataset이 \(N^3\)으로 많아 지게 때문에, FaceNet에서는 Batch안에서 All positive & Hard negative의 Sample을 선택하여 학습하기도 하였다.

이러한 방법들의 가장 큰 문제점은 Generalization이 잘 안된다는 것 이다. 즉, Overfitting이 될 위험이 높다는 것 이다. 이러한 문제점을 해결하기 위하여 해당논문에서는 Quadruplet loss를 제안하였다. 이러한 Loss는 Intra Class간(같은 Class)의 Variation을 줄이고, Inter Class(서로 다른 Class)간의 Variation을 크게함으로 인하여 기존의 Model들보다 Generalization이 잘 된다고 얘기하고 있다.

Introduction

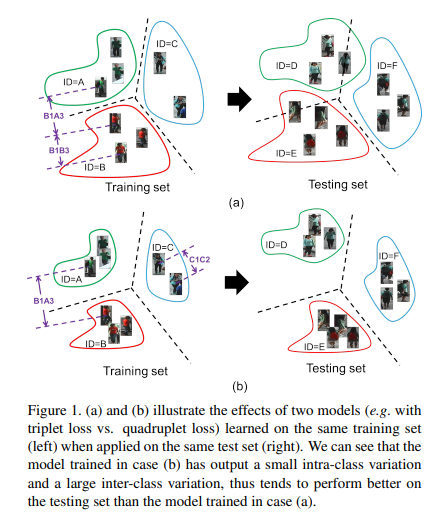
위의 그림은 Abstract에서 지적한 Triplet Loss에 대한 문제점과 해당 논문에서 그러한 문제점을 해결하기 위한 방법에 대한 Figure이다.

먼저 Triplet Loss를 살펴보면 다음과 같다.

$$\text{TripletLoss} = \sum_{i}^N [\|f(x_i^a) - f(x_i^p)\|_2^2 - \| f(x_i^a) - f(x_i^n)\|_2^2 +\alpha]_{+}$$

• \(f(\cdot)\): Feature Extractor
• \(x_i^a, x_i^p, x_i^n\): Anchor, Positive, Negative Sample
• \(\alpha\): Margin

위와 같은 Loss로서 학습하게 되면, Anchor를 기준으로 Positive와 Negative의 Sample간의 거리를 Margin이상으로서 학습하게 된다.
이러한 결과로서 위의 Figure의 (a)와 같이 Inter Class간의 Variation을 크게할 수 있으나, Intra Class간의 Variation은 고려할 수 없다.

해당 논문에서 제시하는 Quadruplet Loss는 이러한 문제를 해결하기 위하여 Figure(b)와 같은 방법을 제시하게 된다. 즉, Inter Class간의 Variation을 크게함과 동시에 Intra Class간의 Variation을 줄이도록 학습한다는 것 이다. 이러한 결과로서 Test set에서 좀 더 Generalization이 잘되는 Model을 얻을 수 있다.

하지만, 이러한 Quadruplet Loss를 사용하게 되면, \(N^3 \rightarrow N^4\)으로서 Dataset이 많아지게 된다. 이러한 문제점을 해결하기 위하여 해당논문은 논문에서 주장하는 Model에서 적합한 Hard Negative Sample을 선택하는 방법에 대해서도 설명하고 있다.

The proposed approach

Notation

• \(\{x_i, x_j, x_k\}\): Triplets // \(x_i\): Anchor, \(x_j\): Positive, \(x_k\): Negative
• \(f(\cdot) \quad(\text{s.t.}\|f(\cdot)\|_2 = 1)\): Feature Extractor
• \(\alpha_{\text{trp}}\): Margin
• \([z]_{+}\) = \(\text{max}(z, 0)\)
• \(g(\cdot)\): Metric -> Dimension으로서 Output이 아닌 Value로서 Output이다. 즉, Euclidian Distance가 아닌 특정 Metric으로서 Output을 구하는 방식

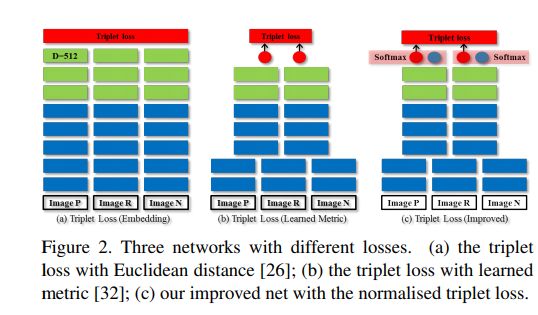
The triplet loss

위의 Figure2는 Triplet Loss를 크게 3가지로서 나타낸 것 이다. 해당논문에서는 (c)를 사용하고 기존의 Triplet Loss를 크게 (a), (b)로서 나누어서 설명하였다.

(a) Distance with Feature Embedding

$$L_{\text{trp}} = \sum_{i,j,k}^N [\|f(x_i) - f(x_j)\|_2^2 - \| f(x_i) - f(x_k)\|_2^2 +\alpha_{\text{trp}}]_{+}$$

기존에 많이 사용하는 Triplet Loss방식이다. Feature Embedidng상에서 같은 Class끼리는 Distance가 가깝게, 다른 CLass끼리는 Distance가 멀게 학습한다.

Figure2(b)의 경우에는 해당 논문에서 제시하는 Model을 살펴보면 이해가 쉽습니다.

The quadruplet loss

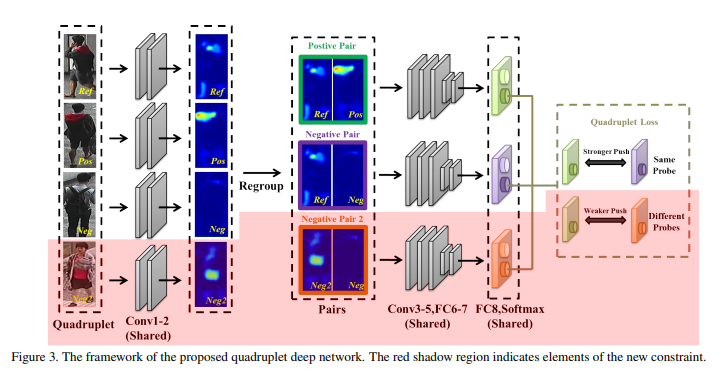
위의 Figure3는 해당논문에서 제시하는 Model이다.

(b) Learned Metric

$$L_{\text{trp}} = \sum_{i,j,k}^N [g(x_i, x_j)^2 - g(x_i, x_k)^2 + \alpha_{\text{trp}}]_{+}$$

위는 기존의 Triplet Loss와 다르게 각각의 Dataset을 Pair로서 학습할때, Distance혹은 Similarity를 측정하는 특정 Metric(\(g(\cdot)\))을 학습하는 방법이다. (해당 논문에서는 Joint Learning of Single-image and Cross-image Representations for Person Re-identification을 예로서 들었습니다.)
위의 Figure3을 살펴보게 되면 이해가 쉽다. 각각의 Dataset은 Pair로 들어가게 되어서, Output으로서 같은 Class혹은 다른 Class로서 판별하여 Output이 나오게 되고 이러한 Output값은 Vector가 아닌 값으로서 표현되게 된다.

(c) Improved
(b)에서 Softmax를 추가한 것이다. 이로 인하여 \(g(x_i, x_j)\)는 [0, 1]의 값을 가지게 되는 Normalization의 효과를 추가할 수 있다.

Proposed Model
3가지의 Triplet Loss중 (c)를 사용하여 Loss를 구성하게 된다. 해당 Quadruplet Loss는 아래와 같은 Formula로서 나타낸다.

$$L_{\text{quad}} = \sum_{i,j,k}^N [g(x_i, x_j)^2 - g(x_i, x_j)^2 + \alpha_1]_{+} + [g(x_i, x_j)^2 - g(x_l, x_k)^2 + \alpha_2]_{+}$$

$$s_i = s_j, s_l \neq s_k, s_i \neq s_l, s_i \neq s_k$$

위의 Loss를 살펴보게 되면, \(g(\cdot)\)은 Dataset이 Pair로 들어갔을 경우 Similarity를 Softmax로서 Normalization되어 나오는 Output이라고 생각할 수 있다.

\(\sum_{i,j,k}^N [g(x_i, x_j)^2 - g(x_i, x_j)^2 + \alpha_1]_{+}\)로 인하여, Inter Class간의 Variation을 크게 하는 Triplet Loss와 동일하다는 것을 알 수 있다. 그와 동시에 \(\sum_{i,j,k}^N [g(x_i, x_j)^2 - g(x_l, x_k)^2 + \alpha_2]_{+}\)로서 Intra Class간의 Variation을 작게하는 것을 살펴볼 수 있다. 또한 \(\alpha_1\)은 상대적으로 크게하여 Inter Class간의 Variation을 크게 하고, \(\alpha_2\)는 상대적으로 작게한다.

참조. \(\alpha_1, \alpha_2\)
상대적으로 \(\alpha_1\)을 크게하고, \(\alpha_2\)는 작게하는 이유를 생각해보면, \(\alpha_2\)의 의미를 생각해보면 된다.

\(\alpha_1\)을 같은 Class의 Distance + Margin으로서 Negative와의 Distance를 결정하게 된다. 하지만, \(\alpha_2\)는 Class의 Distance + Intra Class간의 Distance + Margin으로서 좀 더 큰 Distance로서 학습하는 것을 알 수 있다. 즉, \(\alpha_2\)가 \(\alpha_1\)보다 크게 되면, 앞의 식은 의미가 없어지게 되고, 학습이 Overfitting될 확률이 많이 높은 것을 알 수 있다.

Margin-based online hard negative mining

Abstract에서도 나왔듯이 해당 논문의 Loss는 Intra Class간의 Variation을 줄일 수 있으나, \(\{x_i, x_j, x_k\} \rightarrow \{x_i, x_j, x_k, x_l\}\)로서 Dataset이 너무 많아지게 되는 것을 알 수 있다. 따라서 해당논문에서는 이러한 문제점을 해결하기 위하여 Margin-based online hard negative mining을 적용하였다.

먼저 해당 논문에서 주요하게 생각하는 것은 Adaptive Margin이였다. Hard sample을 선택(참조: Category of Triplet Loss Dataset은 Hard sample에 대하여 적어두었습니다.)할 때 Small, Large Margin의 문제점에 대해서 정의한다.

1. Small Margin \(\rightarrow\) Few Hard Sample \(\rightarrow\) Slow convergence, Easily lead the model to suboptimal solution
2. Large Margin \(\rightarrow\) Many Hard Sample \(\rightarrow\) Overfitting

위와 같은 Underfitting & Overfitting문제를 해결하기 위하여, 적절한 Margin을 선택하기 위해 Adaptive Margin을 적용하였다. Adaptive Margin은 아래 Fomula로 나타낸다.

$$\alpha = w(\mu_n - \mu_p)$$

$$w(\frac{1}{N_n}\sum_{i,k}^N g(x_i, x_k)^2 - \frac{1}{N_p}\sum_{i,j}^N g(x_i, x_j)^2)$$

$$s_i = s_j, s_i \neq s_k$$

위의 식을 살펴보게 되면, \(w\)의 값에 따라서 margin을 선택할 수 있다. 해당 논문에서는 상대적으로 큰 \(\alpha_1\)은 \(w=1\), 상대적으로 작은 \(\alpha_2\)는 \(w=0.5\)로서 Experiment를 실시하였다.

참조: Category of Triplet Loss Dataset
먼저 대중적으로 사용하는 Triplet Loss에서 Easy, Hard, Semi-hard Triplets을 Formula를 살펴보면 다음과 같이 나타낼 수 있다.

• d(a, p) + margin < d(a,n): Easy Sample
• d(a, n) < d(a,p): Hard Sample
• d(a, p) < d(a,n) < d(a, p) + margin: Semi-hard Sample

현재 논문에서는 Semi-hard sample을 Hard sample이라고 표현하고 있다.

Experiment

해당 논문의 결과를 잘 보여주는 Expreiment결과는 아래 Figure이다.

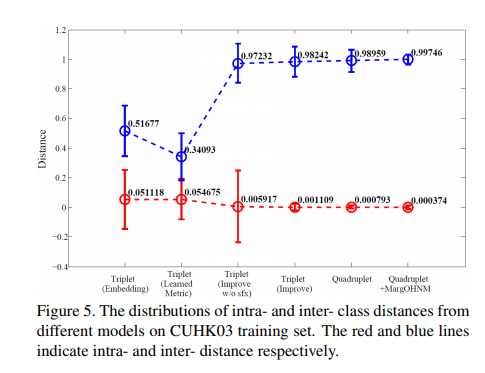
위의 Figure를 살펴보게 되면, Quadraplet Loss는 Inter Class간의 Distance는 Triplet(Improved)와 비슷하나, Intra Class간의 Variation은 매우 작은 것을 살펴볼 수 있다.

Conclusion

해당 논문에서는 Intra Class간의 Variation을 크게하는 Triplet Loss + Inter Class간의 Variation을 작게 하는 추가적인 Loss를 사용하여, Quadruplet Loss를 제안하였다. Generalization에서 좋은 효과를 보여주어서 Performance가 좋은 것을 살펴볼 수 있었다. 하지만, 해당 Loss는 Multiclass에 적용할 수 있지만, Binary Class에서는 적용할 수 없다는 것이 아쉬웠다.

---

참조: Beyond triplet loss: a deep quadruplet network for person re-identification
참조: sooooojinlee GitHub

코드에 문제가 있거나 궁금한 점이 있으면 wjddyd66@naver.com으로 Mail을 남겨주세요.