Tensorflow-Logistic Regression

Logistic Regression

로지스틱 회귀분석은 예측하는 Linear Regression과 달리 Y가 범주형일때 사용하게 된다.
로지스틱 회귀는 이항형 또는 다향형이 될 수 있다. 종속변수의 결과가 2개의 종류라면 이항형, 그 이상이라면 다항형이다.
이항형 다항형에 따라 활성화 함수(active function)이 아래와 같은 종류를 가지게 된다.
이항형: 시그모이드 혹은 하이퍼 볼릭 탄젠트, 다항형: 소프트맥스
로지스틱 회귀분석 자세한 내용

로지스틱 회귀분석에서 활성화 함수를 시그모이드를 사용한다고 하면 아래와 같은 식을 얻을 수 있다.

$$ y(x) = {1 \over 1+e^{-ax+b}}$$

위의 식에서 a값을 변화시켰을 경우 그래프의 기울기를 변화시킬 수 있고, b값을 변화시켜 그래프를 평행이동 시킬 수 있다.
a값을 변화시켰을때의 시그모이드 그래프

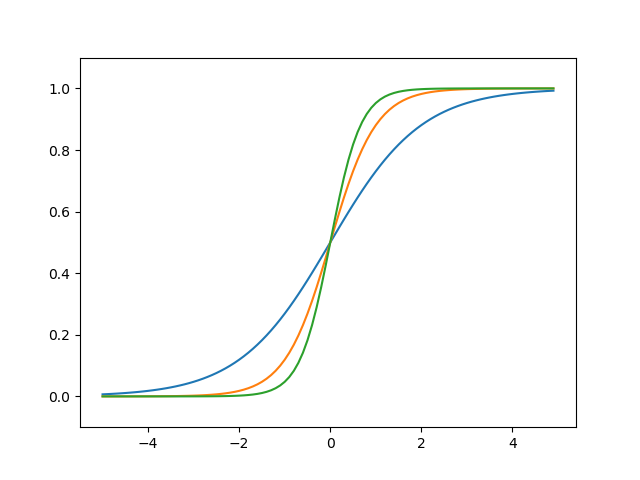
b값을 변화시켰을때의 시그모이드 그래프

Cross Entropy

Logistic Regression또한 Linear Regression과 같이 MSE를 사용하여 구할 수 있으나 Cross Entropy를 사용하여 Model의 성능을 향상시킬 수 있다.
Cross Entropy를 이해하기 위해서 정보량, 엔트로피의 개념을 알고 있어야 한다.

정보량은 아래와 같은 식으로 표현할 수 있다.

$$I(x) = log(\frac{1}{p(x)}) $$

\((1 \over p(x))\) 은 사건이 발생할 수 있는 확률이다.
이러한 값에 log를 취함으로 인하여 필요한 최소한의 자원을 나타낸다.

Entropy는 아래와 같은 식으로 표현할 수 있다.

$$H_p(X)=\sum_{i=0}^n p(x_i)log(p(x_i)) $$

Entropy는 정보량에 대한 기댓값이며 동시에 사건을 표현하기 위해 요구되는 평균 자원이라고 할 수 있다.으로 정의된다.
예측이 어려울수록 정보의 양은 더 많아지고 엔트로피는 더 커진다.

Cross Entropy의식은 아래와 같다.

$$H_{p,q}(x)=\sum_{i=0}^n p(x_i)log(q(x_i)) $$

Entropy는 p는 true label에 대한 분포를, q는 현재 예측모델의 추정값에 대한 분포를 의미하게 된다.
위의 식은 아래와 같은 식으로 나타낼 수 있다.

$$f_c(x)=y\prime log(y) - (1-y\prime)log(1-y) $$

위의 식에서 우변의 값을 각각 따로 그래프로 그려보게 되면 아래와 같다.
\(y\prime log(y)\) 그래프

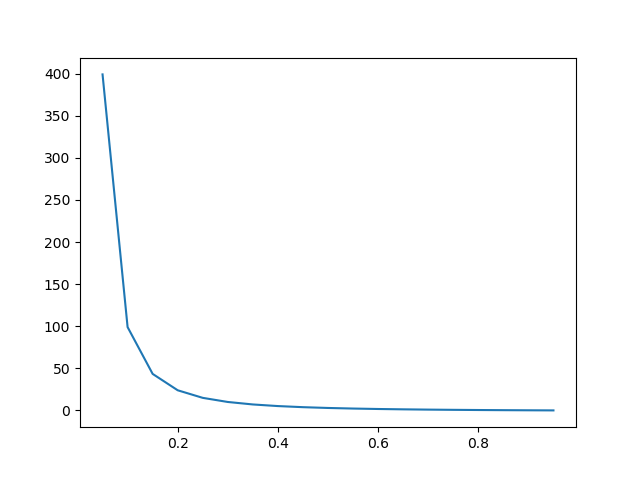
\((1-y\prime)log(1-y)\) 그래프

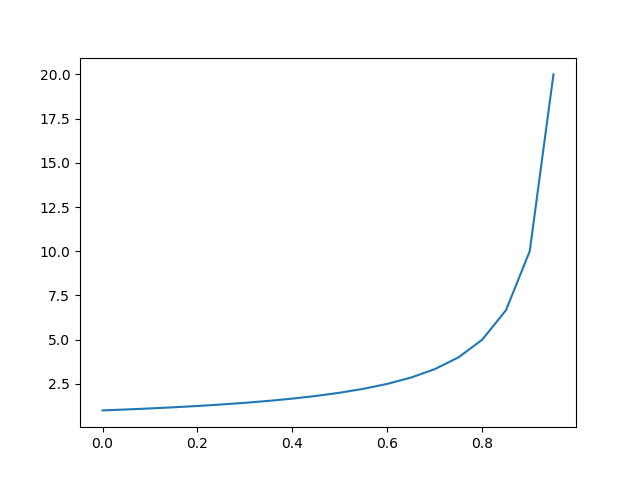
\(y(x) = {1 \over 1+e^{-ax+b}}\) 식에서 a, b값을 조정함에 따라 위의 그래프들의 값이 아래 그림과 같이 변경된다.

서로 값들이 상봔되는 관계를 가지고 있고 두개의 값을 더했을때 가장 작은 값을 찾는것을 목표로 한다.

b에 따른 Cost Function의 식은 아래와 같다.

$$b(update)=b-\alpha\frac{\partial f_c(x)}{\partial b}$$

위의 식을 그래프로 표현하면 아래와 같이 된다고 생각할 수 있다.

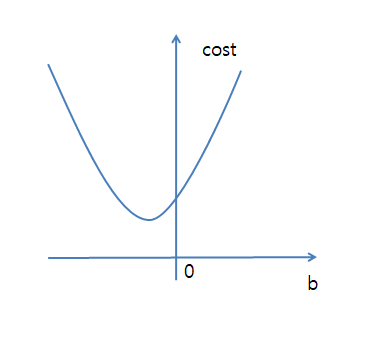
a에 따른 Cost Function의 식은 아래와 같다.

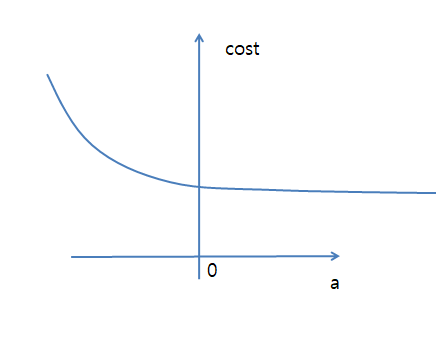
$$a(update)=a-\alpha\frac{\partial f_c(x)}{\partial a}$$

위의 식을 그래프로 표현하면 아래와 같이 된다고 생각할 수 있다.

Softmax-with-Loss계층

Softmax-with-Loss란 Softmax와 Cross Entropy를 합친 계층이라고 할 수 있다. 자세한 Softmax-with-Loss를 알아보기 전에 Loss Function의 사용하는 시기에 대해서 정의해보자.
Loss Function을 사용하는 시기

1. 회귀 분석: MSE
2. 분류 분석: Corss Entropy

분류 분석: Cross Entropy에서 Activation Function의 종류를 사용하는 시기에 대해서 정의해보자.

1. 이항 분류 분석: Sigmoid
2. 다항 분류 분석: Softmax

즉 Softmax-with-Loss계층은 다항 분류 분석에서 사용하는 계층이라는 것을 알 수 있다.

Softmax-with-Loss를 자세히 알아보기 전에 Softmax-with-Loss의 대한 Parameter를 아래와 같이 정의하고 시작하자.

Parameter	의미
$$n$$	분류해야할 범주 수
$$a_i$$	Softmax의 i 번째 입력값
$$p_i$$	Softmax의 i 번째 출력값

또한 앞으로의 내용은 Softmax 의 미분에 대해서는 생략 되어있으므로 아래 링크에서 선행 학습이 필요하다.
Softmax 자세한 내용

Softmax-with-Loss 순전파

• Softmax 출력값

$$p_i = \frac{exp(a_i)}{\sum_n exp(a_n)}$$

• Cross Entropy Loss(L) 값

$$L = -\sum_j y_j logp_j (y_j:Output값)$$

Softmax-with-Loss 역전파

$$\frac{\partial L}{\partial a_i} = \frac{\partial (-\sum_j y_j logp_j)}{\partial a_i}$$

$$ = -\sum_j y_j \frac{\partial logp_j}{\partial a_i}$$

$$ = -\sum_j y_j \frac{1}{p_j} \frac{\partial p_j}{\partial a_i}$$

$$ = -\frac{y_i}{p_i}p_i(1-p_i) - \sum_{i \neq j}\frac{y_j}{p_j}(-p_ip_j)$$

$$ = -y_i + y_ip_i + \sum_{i \neq j}y_jp_i$$

$$= - y_i + p_i\sum_j y_j$$

$$p_i - y_i \text{ }\because(\sum_j y_j = 1)$$

즉 Softmax-with-Loss 노드의 Gradient를 구하려면 입력 벡터에 Softmax를 취한 뒤, 정답 레이블에 해당하는 요소값만 1을 빼주면 된다.
Softmax-with-Loss의 장점

1. Gradient를 구하기 쉽다.
2. Gradient가 0으로 죽는 일이 거의 없다.

Logistic Regression 구현

Logistic Regression 또한 앞선 Post에서 다룬 내용 Linear Regression과 같이 MNIST Data를 분리하는 예제를 사용한다.
이번 MNIST Data의 경우 2가지로 나뉜다.
2가지 경우에 대한 설명과 사용기법은 아래와 같다.

사용 기법	One-Hot-Encodint O	One-Hot-Encodint X
Loss Function	Cross Entropy	Softmax-with-Loss
Optimazation	Gradient Descent	Gradient Descent

One-Hot-Encoding O
Tensorflow import

import tensorflow as tf

MNIST Data Download One-Hot-Encoding O

from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets('/tmp/data/',one_hot=True)

• x: Input Data, Placeholder, Mnist Image flattening => 28 * 28 = 784 shape=[None,784]
• y: Output Data, Placeholder, 1~9 까지의 숫자 판별이므로 shape=[None,10]

flattening: 차원을 1차원으로 바꿔주는 것

x = tf.placeholder(tf.float32,shape=[None,784])
y = tf.placeholder(tf.float32,shape=[None,10])

• Model: y = Wx + b
• W: weight, Variable, shape = [784,10]
• b: bias, Variable, shape = [10]

W = tf.Variable(tf.zeros(shape=[784,10]))
b = tf.Variable(tf.zeros(shape=[10]))
logits = tf.matmul(x,W)+b
y_ = tf.nn.softmax(logits)

• Loss Function: Cross-Entropy
• Optimization: GradientDescent

loss = tf.reduce_mean(-tf.reduce_sum(y*tf.log(y_),reduction_indices=[1]))
train_step = tf.train.GradientDescentOptimizer(0.5).minimize(loss)

Session 및 변수 초기값 할당

sess = tf.Session()
sess.run(tf.global_variables_initializer())

Mnist Data 100개씩 불러와서 Mini-Batch 처리

for i in range(1000):
    batch_xs, batch_ys = mnist.train.next_batch(100)
    sess.run(train_step,feed_dict={x:batch_xs,y:batch_ys})

Model의 정확도 측정 & Session 닫기

correct_prediction = tf.equal(tf.argmax(y_,1),tf.argmax(y,1))
accuracy = tf.reduce_mean(tf.cast(correct_prediction,tf.float32))
print('정확도(Accuracy): %f'%sess.run(accuracy,feed_dict={x:mnist.test.images, y:mnist.test.labels}))

sess.close()

정확도(Accuracy): 0.916800

One-Hot-Encodint X(Label 사용)
MNIST Data Download One-Hot-Encoding X

from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets('/tmp/data/',one_hot=False)

y가 One-Hot-Encoding이아닌 Label이므로 2차원이 아닌 1차원으로 선언

x = tf.placeholder(tf.float32,shape=[None,784])
y = tf.placeholder(tf.int64,shape=[None])
W = tf.Variable(tf.zeros(shape=[784,10]))
b = tf.Variable(tf.zeros(shape=[10]))
logits = tf.matmul(x,W)+b
y_ = tf.nn.softmax(logits)

Loss Function으로 softmax_cross_entropy사용
주의 사항: Label은 항상 int형만 가능하다.

loss = tf.reduce_mean(tf.nn.sparse_softmax_cross_entropy_with_logits(logits=logits, labels=y))
train_step = tf.train.GradientDescentOptimizer(0.5).minimize(loss)

sess = tf.Session()
sess.run(tf.global_variables_initializer())

for i in range(1000):
    batch_xs, batch_ys = mnist.train.next_batch(100)
    sess.run(train_step,feed_dict={x:batch_xs,y:batch_ys})

y가 Label 형태의 Scalar이므로 tf.argmax 사용 X

correct_prediction = tf.equal(tf.argmax(y_,1),y)
accuracy = tf.reduce_mean(tf.cast(correct_prediction,tf.float32))
print('정확도(Accuracy): %f'%sess.run(accuracy,feed_dict={x:mnist.test.images, y:mnist.test.labels}))

sess.close()

정확도(Accuracy): 0.918800

---

참조: 원본코드
참조: 텐서플로로 배우는 딥러닝
참조: Chanwoo Timothy Lee Youtube
참조: curt-park 블로그
문제가 있거나 궁금한 점이 있으면 wjddyd66@naver.com으로 Mail을 남겨주세요.